Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T08:58:17.625Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTRADA INDEX OF GENERAL WEIGHTED GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  28 September 2012

YILUN SHANG
YILUN SHANG*
Affiliation:
Institute for Cyber Security, University of Texas at San Antonio, San Antonio, Texas 78249, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

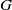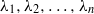Let $G$ be a general weighted graph (with possible self-loops) on $n$ vertices and $\lambda _1,\lambda _2,\ldots ,\lambda _n$ be its eigenvalues. The Estrada index of 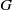$G$ is a graph invariant defined as 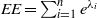$EE=\sum _{i=1}^ne^{\lambda _i}$. We present a generic expression for 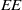$EE$ based on weights of short closed walks in 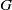$G$. We establish lower and upper bounds for 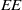$EE$in terms of low-order spectral moments involving the weights of closed walks. A concrete example of calculation is provided.

Keywords

Estrada indexweighted graphspectral momentgraph spectrum

MSC classification

Secondary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 106 - 112
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Biggs, N., Algebraic Graph Theory (Cambridge University Press, Cambridge, 1993).Google Scholar
[2]Caldarelli, G. & Vespignani, A., Large Scale Structure and Dynamics of Complex Networks: From Information Technology to Finance and Natural Science (World Scientific, Singapore, 2007).CrossRefGoogle Scholar
[3]Cvetković, D. M., Doob, M., Gutman, I. & Torgašev, A., Recent Results in the Theory of Graph Spectra (North-Holland, Amsterdam, 1988).Google Scholar
[4]de la Peña, J. A., Gutman, I. & Rada, J., ‘Estimating the Estrada index’, Linear Algebra Appl. 427 (2007), 70–76.CrossRefGoogle Scholar
[5]Du, Z. & Zhou, B., ‘The Estrada index of trees’, Linear Algebra Appl. 435 (2011), 2462–2467.CrossRefGoogle Scholar
[6]Estrada, E., ‘Characterization of 3D molecular structure’, Chem. Phys. Lett. 319 (2000), 713–718.CrossRefGoogle Scholar
[7]Estrada, E., ‘Characterization of the folding degree of proteins’, Bioinformatics 18 (2002), 697–704.CrossRefGoogle ScholarPubMed
[8]Estrada, E., ‘Characterization of the amino acid contribution to the folding degree of proteins’, Proteins 54 (2004), 727–737.CrossRefGoogle Scholar
[9]Estrada, E. & Rodríguez-Velázquez, J. A., ‘Subgraph centrality in complex networks’, Phys. Rev. E 71 (2005), 056103.CrossRefGoogle ScholarPubMed
[10]Estrada, E. & Rodríguez-Velázquez, J. A., ‘Spectral measures of bipartivity in complex networks’, Phys. Rev. E 72 (2005), 046105.CrossRefGoogle ScholarPubMed
[11]Estrada, E., Rodríguez-Velázquez, J. A. & Randić, M., ‘Atomic branching in molecules’, Int. J. Quantum Chem. 106 (2006), 823–832.CrossRefGoogle Scholar
[12]Gutman, I., ‘Lower bounds for Estrada index’, Publ. Inst. Math. Beograd (N.S.) 83 (2008), 1–7.CrossRefGoogle Scholar
[13]Gutman, I. & Graovac, A., ‘Estrada index of cycles and paths’, Chem. Phys. Lett. 436 (2007), 294–296.CrossRefGoogle Scholar
[14]Gutman, I. & Radenković, S., ‘A lower bound for the Estrada index of bipartite molecular graphs’, Kragujevac J. Sci. 29 (2007), 67–72.Google Scholar
[15]Ilić, A. & Stevanović, D., ‘The Estrada index of chemical trees’, J. Math. Chem. 47 (2010), 305–314.CrossRefGoogle Scholar
[16]Liu, J. & Liu, B., ‘Bounds of the Estrada index of graphs’, Appl. Math. J. Chinese Univ. 25 (2010), 325–330.CrossRefGoogle Scholar
[17]Shang, Y., ‘Perturbation results for the Estrada index in weighted networks’, J. Phys. A: Math. Theor. 44 (2011), 075003.CrossRefGoogle Scholar
[18]Shang, Y., ‘Local natural connectivity in complex networks’, Chin. Phys. Lett. 28 (2011), 068903.CrossRefGoogle Scholar
[19]Shang, Y., ‘The Estrada index of random graphs’, Sci. Magna 7 (2011), 79–81.Google Scholar
[20]Shang, Y., ‘Biased edge failure in scale-free networks based on natural connectivity’, Indian J. Phys. 86 (2012), 485–488.CrossRefGoogle Scholar
[21]Zhou, B., ‘On Estrada index’, MATCH Commun. Math. Comput. Chem. 60 (2008), 485–492.Google Scholar
[22]Zhou, B. & Du, Z., ‘Some lower bounds for Estrada index’, Iran. J. Math. Chem. 1 (2010), 67–72.Google Scholar
[23]Zhou, B. & Trinajstić, N., ‘Estrada index of bipartite graphs’, Int. J. Chem. Model 1 (2008), 387–394.Google Scholar