Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T18:12:43.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirichlet series with positive real part

Published online by Cambridge University Press:  17 April 2009

N. Samaris
N. Samaris
Affiliation:
Department of Mathematics, University of Patras, 261–10 Patras, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the sequence Λ = {0 < λ2 < λ2 < …}, for which λn → +∞. We denote by PD(Λ) the class of Dirichlet's series having the form F(s) = 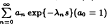defined in the half plan Re s > 0 converging absolutely and Re F ≥ 0. If N0 = {0, 1,2, …} then the class PD(N0) coincides with the Caratheodory's class P. In this paper some classical results holding for the class P are generalised in any class PD(Λ). In special cases for the sequence Λ extreme problems are examined in the class PD(Λ).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 46 , Issue 1 , August 1992 , pp. 159 - 166
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Artemiadis, N., ‘Quelques resultat sur les transformees de Fourier avec applications’, Bull. Sc. Math. 97 (1973), 177–191.Google Scholar
[2]Holland, F., ‘The extreme points of a class of functions with positive real part’, Math. Ann. 202 (1973), 85–87.CrossRefGoogle Scholar
[3]Katznelson, Y., An introduction to harmonic analysis (John Wiley and Sons. Inc., New York, 1968).Google Scholar