Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T04:07:15.690Z Has data issue: false hasContentIssue false
  • English
  • Français

DIFFERENTIATING SOLUTIONS OF A BOUNDARY VALUE PROBLEM ON A TIME SCALE

Part of: Boundary value problems Dynamic equations on time scales or measure chains

Published online by Cambridge University Press:  01 April 2016

LEE H. BAXTER ,
JEFFREY W. LYONS  and
JEFFREY T. NEUGEBAUER
LEE H. BAXTER
Affiliation:
Department of Mathematics and Statistics, Eastern Kentucky University, Richmond, KY 40475, USA email [email protected]
JEFFREY W. LYONS
Affiliation:
Division of Math, Science and Technology, Nova Southeastern University, Fort Lauderdale, FL 33314, USA email [email protected]
JEFFREY T. NEUGEBAUER*
Affiliation:
Department of Mathematics and Statistics, Eastern Kentucky University, Richmond, KY 40475, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the solution of the dynamic boundary value problem 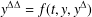$y^{{\rm\Delta}{\rm\Delta}}=f(t,y,y^{{\rm\Delta}})$, 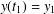$y(t_{1})=y_{1}$, 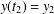$y(t_{2})=y_{2}$, on a general time scale, may be delta-differentiated with respect to 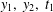$y_{1},~y_{2},~t_{1}$ and 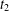$t_{2}$. By utilising an analogue of a theorem of Peano, we show that the delta derivative of the solution solves the boundary value problem consisting of either the variational equation or its dynamic analogue along with interesting boundary conditions.

Keywords

time scalesvariational equationuniqueness

MSC classification

Primary: 34N05: Dynamic equations on time scales or measure chains
Secondary: 34B99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 101 - 109
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Benchohra, M., Hamani, S., Henderson, J., Ntouyas, S. K. and Ouahab, A., ‘Differentiation and differences for solutions of nonlocal boundary value problems for second order difference equations’, Int. J. Differ. Equ. 2(1) (2007), 37–47.Google Scholar
Bohner, M. and Peterson, A., Dynamic Equations on Time Scales: An Introduction with Applications (Birkhäuser, Boston, 2001).Google Scholar
Bohner, M. and Peterson, A. (eds.), Advances in Dynamic Equations on Time Scales (Birkhäuser, Boston, 2003).CrossRefGoogle Scholar
Chyan, C. J., ‘Uniqueness implies existence on time scales’, J. Math. Anal. Appl. 258(1) (2001), 359–365.Google Scholar
Datta, A., ‘Differences with respect to boundary points for right focal boundary conditions’, J. Difference Equ. Appl. 4 (1998), 571–578.Google Scholar
Ehme, J., ‘Differentiation of solutions of boundary value problems with respect to nonlinear boundary conditions’, J. Differential Equations 101 (1993), 139–147.Google Scholar
Ehrke, J., Henderson, J., Kunkel, C. and Sheng, Q., ‘Boundary data smoothness for solutions of nonlocal boundary value problems for second order differential equations’, J. Math. Anal. Appl. 333(1) (2007), 191–203.Google Scholar
Hartman, P., Ordinary Differential Equations (Wiley, New York, 1964).Google Scholar
Henderson, J., ‘Right focal point boundary value problems for ordinary differential equations and variational equations’, J. Math. Anal. Appl. 98(2) (1984), 363–377.Google Scholar
Henderson, J., ‘Disconjugacy, disfocality, and differentiation with respect to boundary conditions’, J. Math. Anal. Appl. 121(1) (1987), 1–9.Google Scholar
Henderson, J., Hopkins, B., Kim, E. and Lyons, J. W., ‘Boundary data smoothness for solutions of nonlocal boundary value problems for nth order differential equations’, Involve 1(2) (2008), 167–181.CrossRefGoogle Scholar
Henderson, J., Horn, M. and Howard, L., ‘Differentiation of solutions of difference equations with respect to boundary values and parameters’, Comm. Appl. Nonlinear Anal. 1(2) (1994), 47–60.Google Scholar
Hopkins, B., Kim, E., Lyons, J. W. and Speer, K., ‘Boundary data smoothness for solutions of nonlocal boundary value problems for second order difference equations’, Comm. Appl. Nonlinear Anal. 2(2) (2009), 1–12.Google Scholar
Janson, A. F., Juman, B. T. and Lyons, J. W., ‘The connection between variational equations and solutions of second order nonlocal integral boundary value problems’, Dynam. Systems Appl. 23(2–3) (2014), 493–504.Google Scholar
Lakshmikantham, V., Sivasundaram, S. and Kaymakçalan, B., Dynamic Systems on Measure Chains (Kluwer Academic Publishers, Boston, 1996).Google Scholar
Lyons, J. W., ‘Differentiation of solutions of nonlocal boundary value problems with respect to boundary data’, Electron. J. Qual. Theory Differ. Equ. 2011(51) (2011), 1–11.CrossRefGoogle Scholar
Lyons, J. W., ‘Disconjugacy, differences, and differentiation for solutions of nonlocal boundary value problems for nth order difference equations’, J. Difference Equ. Appl. 20(2) (2014), 296–311.Google Scholar
Lyons, J. W., ‘On differentiation of solutions of boundary value problems for second order dynamic equations on a time scale’, Comm. Appl. Anal. 18 (2014), 215–224.Google Scholar
Peterson, A., ‘Comparison theorems and existence theorems for ordinary differential equations’, J. Math. Appl. 55 (1976), 773–784.Google Scholar
Spencer, J., ‘Relations between boundary value functions for a nonlinear differential equation and its variational equations’, Canad. Math. Bull. 18(2) (1975), 269–276.CrossRefGoogle Scholar