Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T21:19:44.426Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREE-ONE MAHLER FUNCTIONS: ASYMPTOTICS, APPLICATIONS AND SPECULATIONS

Part of: Sequences and sets Discrete mathematics in relation to computer science Diophantine approximation, transcendental number theory Series expansions

Published online by Cambridge University Press:  05 February 2020

MICHAEL COONS Open the ORCID record for MICHAEL COONS [Opens in a new window]
MICHAEL COONS*
Affiliation:
School of Mathematical and Physical Sciences,University of Newcastle, Callaghan, NSW 2308, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a complete characterisation of the radial asymptotics of degree-one Mahler functions as $z$ approaches roots of unity of degree 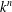$k^{n}$, where 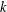$k$ is the base of the Mahler function, as well as some applications concerning transcendence and algebraic independence. For example, we show that the generating function of the Thue–Morse sequence and any Mahler function (to the same base) which has a nonzero Mahler eigenvalue are algebraically independent over 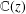$\mathbb{C}(z)$. Finally, we discuss asymptotic bounds towards generic points on the unit circle.

Keywords

transcendencealgebraic independenceradial asymptoticsautomatic sequencesMahler functions

MSC classification

Primary: 11J91: Transcendence theory of other special functions
Secondary: 11B85: Automata sequences 30B10: Power series (including lacunary series) 68R15: Combinatorics on words
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 399 - 409
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamczewski, B., Dreyfus, T. and Hardouin, C., ‘Hypertranscendence and linear difference equations’, Preprint, 2019.Google Scholar
Allouche, J.-P. and Shallit, J., Automatic Sequences (Cambridge University Press, Cambridge, 2003).10.1017/CBO9780511546563CrossRefGoogle Scholar
Bell, J. P. and Coons, M., ‘Transcendence tests for Mahler functions’, Proc. Amer. Math. Soc. 145(3) (2017), 1061–1070.CrossRefGoogle Scholar
Bundschuh, P., ‘Algebraic independence of infinite products and their derivatives’, in: Number Theory and Related Fields, Springer Proceedings in Mathematics and Statistics, 43 (Springer, New York, 2013), 143–156.10.1007/978-1-4614-6642-0_6CrossRefGoogle Scholar
Bundschuh, P. and Väänänen, K., ‘On certain Mahler functions’, Acta Math. Hungar. 145(1) (2015), 150–158.CrossRefGoogle Scholar
Bundschuh, P. and Väänänen, K., ‘Arithmetic properties of infinite products of cyclotomic polynomials’, Bull. Aust. Math. Soc. 93(3) (2016), 375–387.10.1017/S0004972715001550CrossRefGoogle Scholar
Bundschuh, P. and Väänänen, K., ‘Hypertranscendence and algebraic independence of certain infinite products’, Acta Arith. 184(1) (2018), 51–66.10.4064/aa170528-16-12CrossRefGoogle Scholar
Bundschuh, P. and Väänänen, K., ‘Note on the Stern–Brocot sequence, some relatives, and their generating power series’, J. Théor. Nombres Bordeaux 30(1) (2018), 195–202.10.5802/jtnb.1022CrossRefGoogle Scholar
Cobham, A., ‘Uniform tag sequences’, Math. Syst. Theory 6 (1972), 164–192.10.1007/BF01706087CrossRefGoogle Scholar
Coons, M., ‘An asymptotic approach in Mahler’s method’, New Zealand J. Math. 47 (2017), 27–42.Google Scholar
Coons, M. and Tachiya, Y., ‘Transcendence over meromorphic functions’, Bull. Aust. Math. Soc. 95(3) (2017), 393–399.10.1017/S0004972717000193CrossRefGoogle Scholar
de Bruijn, N. G., ‘On Mahler’s partition problem’, Nederl. Akad. Wetensch. Proc. 51 (1948), 659–669; Indag. Math. (N.S.) 10 (1948), 210–220.Google Scholar
Duffin, R. J. and Schaeffer, A. C., ‘Power series with bounded coefficients’, Amer. J. Math. 67 (1945), 141–154.10.2307/2371922CrossRefGoogle Scholar
Duke, W. and Nguyen, H. N., ‘Infinite products of cyclotomic polynomials’, Bull. Aust. Math. Soc. 91(3) (2015), 400–411.CrossRefGoogle Scholar
Loxton, J. H. and Van der Poorten, A. J., ‘Transcendence and algebraic independence by a method of Mahler’, in: Transcendence Theory: Advances and Applications, Proc. Conf. Univ. Cambridge 1976 (eds. Baker, A. and Masser, D. W.) (Academic Press, London, 1977), 211–226.Google Scholar
Mahler, K., ‘The spectrum of an array and its application to the study of the translation properties of a simple class of arithmetical functions, II: On the translation properties of a simple class of arithmetical functions’, J. Math. Phys. Mass. Inst. Techn. 6 (1927), 158–163.Google Scholar
Mahler, K., ‘Arithmetische Eigenschaften der Lösungen einer Klasse von Funktionalgleichungen’, Math. Ann. 101 (1929), 342–366.CrossRefGoogle Scholar
Mahler, K., ‘Über das Verschwinden von Potenzreihen mehrerer Veränderlicher in speziellen Punktfolgen’, Math. Ann. 103 (1930), 573–587.CrossRefGoogle Scholar
Mahler, K., ‘Arithmetische Eigenschaften einer Klasse transzendental-transzendenter Funktionen’, Math. Z. 32 (1930), 545–585.CrossRefGoogle Scholar
Mahler, K., ‘On some inequalities for polynomials in several variables’, J. Lond. Math. Soc. 37 (1962), 341–344.CrossRefGoogle Scholar
Mahler, K., ‘Fifty years as a mathematician’, J. Number Theory 14 (1982), 121–155.CrossRefGoogle Scholar
Nishioka, Ku., ‘Algebraic independence by Mahler’s method and S-unit equations’, Compos. Math. 92 (1994), 87–110.Google Scholar