Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T21:29:07.292Z Has data issue: false hasContentIssue false
  • English
  • Français

CRITERIA FOR THE SEQUENCE OF DIFFERENCES OF A BOUNDED SEQUENCE TO BE NULL

Part of: Convergence and divergence of infinite limiting processes

Published online by Cambridge University Press:  17 September 2012

DAVID BORWEIN
DAVID BORWEIN*
Affiliation:
Department of Mathematics, Western University, London ON, Canada N6A 5B7 (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Conditions are established for the sequence of differences $\{a_n-a_{n-1}\}$ of a bounded sequence 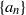$\{a_n\}$ of complex terms to converge to zero when a certain linear nonhomogeneous difference expression of the form 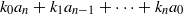$k_0 a_n+k_1a_{n-1}+\cdots +k_na_0$tends to zero as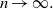$n\to \infty .$

Keywords

sequenceboundedlinear nonhomogeneous difference expression

MSC classification

Secondary: 40A05: Convergence and divergence of series and sequences
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 123 - 127
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Borwein, D., ‘Convergence criteria for bounded sequences’, Proc. Edinb. Math. Soc. 18 (1972), 99–103.CrossRefGoogle Scholar
[2]Copson, E. T., ‘On a generalisation of monotonic sequences’, Proc. Edinb. Math. Soc. 17 (1970), 159–164.CrossRefGoogle Scholar
[3]Stević, S., ‘A note on bounded sequences satisfying linear inequality’, Indian J. Math. 43 (2001), 223–230.Google Scholar
[4]Stević, S., ‘A note on bounded sequences satisfying linear nonhomogeneous difference equation’, Indian J. Math. 45 (2003), 357–367.Google Scholar
[5]Zygmund, A., Trigonometric Series, 1 (Cambridge University Press, Cambridge, 1959).Google Scholar