Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T06:02:03.111Z Has data issue: false hasContentIssue false
  • English
  • Français

CONVEX STANDARD FUNDAMENTAL DOMAIN FOR SUBGROUPS OF HECKE GROUPS

Part of: Other groups of matrices Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 September 2010

BOUBAKARI IBRAHIMOU  and
OMER YAYENIE
BOUBAKARI IBRAHIMOU
Affiliation:
Murray State University, 6C-19 Faculty Hall, Murray, KY 42071, USA (email: [email protected])
OMER YAYENIE*
Affiliation:
Murray State University, 6C-1 Faculty Hall, Murray, KY 42071, USA (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that if a convex hyperbolic polygon is constructed as a fundamental domain for a subgroup of SL(2,ℝ), then its translates by the group form a locally finite tessellation and its side-pairing transformations form a system of generators for the group. Such a hyperbolically convex fundamental domain for any discrete subgroup can be obtained by using Dirichlet’s and Ford’s polygon constructions. However, these two results are not well adapted for the actual construction of a hyperbolically convex fundamental domain due to their nature of construction. A third, and most important and practical, method of obtaining a fundamental domain is through the use of a right coset decomposition as described below. If Γ2 is a subgroup of Γ1 such that Γ1=Γ2⋅{L1,L2,…,Lm} and 𝔽 is the closure of a fundamental domain of the bigger group Γ1, then the set 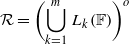is a fundamental domain of Γ2. One can ask at this juncture, is it possible to choose the right coset suitably so that the set ℛ is a convex hyperbolic polygon? We will answer this question affirmatively for Hecke modular groups.

Keywords

fundamental domainHecke modular groupsh-convex setmodular group

MSC classification

Secondary: 11F06: Structure of modular groups and generalizations; arithmetic groups 20H05: Unimodular groups, congruence subgroups 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 83 , Issue 1 , February 2011 , pp. 96 - 107
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Beardon, A. L., The Geometry of Discrete Groups, Graduate Texts in Mathematics, 91 (Springer, New York, 1983).CrossRefGoogle Scholar
[2]Cangül, I. N., ‘The group structure of Hecke groups H(λq)’, Turkish J. Math. 20(2) (1996), 203–207.Google Scholar
[3]Cangül, I. N., ‘About some normal subgroups of Hecke groups’, Turkish J. Math. 21 (1997), 143–151.Google Scholar
[4]Evans, R. J., ‘A fundamental region for Hecke’s modular groups’, J. Number Theory 5 (1973), 108–115.CrossRefGoogle Scholar
[5]Ford, L., Automorphic Functions (McGraw-Hill, New York, 1929).Google Scholar
[6]Hecke, E., ‘Über die Bestimmung Dirichletscher Reichen durch ihre Funktionalgleichungen’, Math. Ann. 112 (1936), 664–699.CrossRefGoogle Scholar
[7]Huang, S., ‘Generalized Hecke groups and Hecke polygons’, Ann. Acad. Sci. Fenn. Math. 24 (1999), 187–214.Google Scholar
[8]Keskin, R., ‘On the parabolic class numbers of some subgroups of Hecke groups’, Turkish J. Math. 22 (1998), 199–205.Google Scholar
[9]Knopp, M. I., Modular Functions in Analytic Number Theory (American Mathematical Society, Providence, RI, 1993).Google Scholar
[10]Kulkarni, R. S., ‘An arithmetic geometric method in the study of the subgroups of the modular group’, Amer. J. Math. 113 (1991), 1053–1133.CrossRefGoogle Scholar
[11]Lang, M. L., ‘Independent generators for congruence subgroups of Hecke groups’, Math. Z. 200(4) (1995), 569–594.CrossRefGoogle Scholar
[12]Lang, M. L., ‘The signatures of the congruence subgroups G 0(τ) of the Hecke groups G 4 and G 6’, Comm. Algebra 28(8) (2000), 3691–3702.CrossRefGoogle Scholar
[13]Lehner, J., Discontinuous Groups and Automorphic Functions (American Mathematical Society, Providence, RI, 1964).CrossRefGoogle Scholar
[14]Leutbecher, A., ‘Über die Heckeschen Gruppen G(λ)’, Abh. Math. Sem. Hamburg 31 (1967), 199–205.CrossRefGoogle Scholar
[15]Leutbecher, A., ‘Über die Heckeschen Gruppen G(λ), II’, Math. Ann. 211 (1974), 63–68.CrossRefGoogle Scholar
[16]Newman, M., ‘Free subgroups and normal subgroups of the modular group’, Illinois J. Math. 8 (1964), 262–265.CrossRefGoogle Scholar
[17]Newman, M., ‘A complete description of the normal subgroups of genus one of the modular group’, Amer. J. Math. 86 (1964), 17–24.CrossRefGoogle Scholar
[18]Newman, M., ‘Normal subgroups of the modular group which are not congruence subgroups’, Proc. Amer. Math. Soc. 16 (1965), 831–832.CrossRefGoogle Scholar
[19]Parson, L. A., ‘Generalized Kloosterman sums and the Fourier coefficients of cusp forms’, Trans. Amer. Math. Soc. 217 (1976), 329–350.CrossRefGoogle Scholar
[20]Parson, L. A., ‘Normal congruence subgroups of the Hecke groups and ’, Pacific J. Math. 70 (1977), 481–487.CrossRefGoogle Scholar
[21]Rademacher, H., ‘Über die Erzeugenden der Kongruenzuntergruppen der Modulgruppe’, Abh. Math. Sem. Hamburg 7 (1929), 134–148.CrossRefGoogle Scholar
[22]Rankin, R. A., The Modular Group and its Subgroups (Ramanujan Institute, Madras, 1969).Google Scholar
[23]Schoeneberg, B., Elliptic Modular Functions, Die Grundlehren der mathematische Wissenschaften in Einzeldarstellungen, Band 203 (Springer, Berlin, 1974).CrossRefGoogle Scholar
[24]Tietz, H., ‘Über Konvexheit im kleinen und im großen und über gewissen den Punkten einer Menge zugeordnete Dimensionszahlen’, Math. Z. 28 (1928), 697–707.CrossRefGoogle Scholar
[25]Yayenie, O., ‘Subgroups of some Fuchsian groups defined by two linear congruences’, Conform. Geom. Dyn. 11 (2007), 271–287.CrossRefGoogle Scholar
[26]Yayenie, O., ‘Nonexistence of cuspidal fundamental domain’, Bull. Korean Math. Soc. 46(5) (2009), 823–833.CrossRefGoogle Scholar
[27]Young, J., ‘On the group of sign (0,3;2,4,∞) and the functions belonging to it’, Trans. Amer. Math. Soc. 5 (1904), 81–104.Google Scholar
[28]Zagier, D., ‘Modular parametrization of elliptic curves’, Canad. Math. Bull. 28 (1985), 372–384.CrossRefGoogle Scholar