Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T18:59:26.926Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSTRUCTION OF NORMAL NUMBERS USING THE DISTRIBUTION OF THE 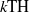$k\rm TH$ LARGEST PRIME FACTOR

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Elementary number theory

Published online by Cambridge University Press:  31 October 2012

JEAN-MARIE DE KONINCK  and
IMRE KÁTAI
JEAN-MARIE DE KONINCK*
Affiliation:
Dép. de mathématiques et de statistique, Université Laval, Québec, Canada G1V 0A6 (email: [email protected])
IMRE KÁTAI
Affiliation:
Computer Algebra Department, Eötvös Loránd University, 1117 Budapest, Pázmány Péter Sétány I/C, Hungary (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

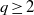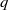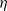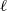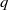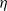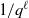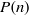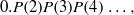Given an integer $q\ge 2$, a $q$-normal number is an irrational number $\eta $ such that any preassigned sequence of $\ell $ digits occurs in the $q$-ary expansion of $\eta $ at the expected frequency, namely $1/q^\ell $. In a recent paper we constructed a large family of normal numbers, showing in particular that, if $P(n)$ stands for the largest prime factor of $n$, then the number $0.P(2)P(3)P(4)\ldots ,$ the concatenation of the numbers 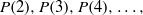$P(2), P(3), P(4), \ldots ,$ each represented in base 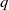$q$, is a 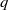$q$-normal number, thereby answering in the affirmative a question raised by Igor Shparlinski. We also showed that 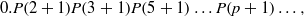$0.P(2+1)P(3+1)P(5+1) \ldots P(p+1)\ldots ,$ where 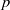$p$ runs through the sequence of primes, is a 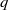$q$-normal number. Here, we show that, given any fixed integer 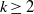$k\ge 2$, the numbers 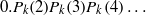$0.P_k(2)P_k(3)P_k(4)\ldots $ and 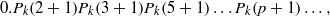$0. P_k(2+1)P_k(3+1)P_k(5+1) \ldots P_k(p+1)\ldots ,$ where 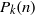$P_k(n)$ stands for the 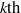$k{\rm th}$ largest prime factor of $n$, are 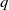$q$-normal numbers. These results are part of more general statements.

Keywords

normal numberslargest prime factor

MSC classification

Secondary: 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc. 11A41: Primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 158 - 168
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Bassily, N. L. & Kátai, I., ‘Distribution of consecutive digits in the $q$-ary expansions of some sequences of integers’, J. Math. Sci. 78(1) (1996), 11–17.CrossRefGoogle Scholar
[2]De Koninck, J. M. & Kátai, I., ‘On a problem on normal numbers raised by Igor Shparlinski’, Bull. Aust. Math. Soc. 84 (2011), 337–349.CrossRefGoogle Scholar
[3]De Koninck, J. M. & Luca, F., Analytic Number Theory: Exploring the Anatomy of Integers, Graduate Studies in Mathematics, 134 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
[4]Halberstam, H. H. & Richert, H. E., Sieve Methods (Academic Press, London, 1974).Google Scholar