Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T20:58:47.028Z Has data issue: false hasContentIssue false
  • English
  • Français

THE BAIRE PROPERTY IN THE REMAINDERS OF SEMITOPOLOGICAL GROUPS

Part of: Spaces with richer structures Basic constructions Generalities

Published online by Cambridge University Press:  21 January 2013

LI-HONG XIE  and
SHOU LIN
LI-HONG XIE*
Affiliation:
School of Mathematics, Sichuan University, Chengdu 610065, PR China
SHOU LIN
Affiliation:
Department of Mathematics, Zhangzhou Normal University, Zhangzhou 363000, PR China Institute of Mathematics, Ningde Normal University, Ningde 352100, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is proved that every remainder of a nonlocally compact semitopological group 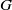$G$ is a Baire space if and only if 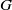$G$ is not Čech-complete, which improves a dichotomy theorem of topological groups by Arhangel’skiǐ [‘The Baire property in remainders of topological groups and other results’, Comment. Math. Univ. Carolin. 50(2) (2009), 273–279], and also gives a positive answer to a question of Lin and Lin [‘About remainders in compactifications of paratopological groups’, ArXiv: 1106.3836v1 [Math. GN] 20 June 2011]. We also show that for a nonlocally compact rectifiable space 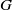$G$ every remainder of 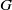$G$ is either Baire, or meagre and Lindelöf.

Keywords

semitopological groupsrectifiable spacesremaindersdichotomy theoremsBaire spacesp-spaces

MSC classification

Secondary: 54A25: Cardinality properties (cardinal functions and inequalities, discrete subsets) 54B05: Subspaces 54E20: Stratifiable spaces, cosmic spaces, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 301 - 308
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Arhangel’skiǐ, A. V., ‘$D$-spaces and covering properties’, Topology Appl. 146–147 (2005), 437–449.CrossRefGoogle Scholar
Arhangel’skiǐ, A. V., ‘Remainders in compactifications and generalized metrizability properties’, Topology Appl. 150 (2005), 79–90.CrossRefGoogle Scholar
Arhangel’skiǐ, A. V., ‘Two types of remainders of topological groups’, Comment. Math. Univ. Carolin. 49 (2008), 119–126.Google Scholar
Arhangel’skiǐ, A. V., ‘The Baire property in remainders of topological groups and other results’, Comment. Math. Univ. Carolin. 50 (2) (2009), 273–279.Google Scholar
Arhangel’skiǐ, A. V., ‘Some aspects of topological algebra and remainders of topological groups’, Topology Proc. 33 (2009), 13–28.Google Scholar
Arhangel’skiǐ, A. V. and Choban, M. M., ‘On remainders of rectifiable spaces’, Topology Appl. 157 (2010), 789–799.CrossRefGoogle Scholar
Arhangel’skiǐ, A. V. and Choban, M. M., ‘Completeness type properties of semitopological groups, and the theorems of Montgomery and Ellis’, Topology Proc. 37 (2011), 33–60.Google Scholar
Arhangel’skiǐ, A. V. and Tkachenko, M. G., Topological Groups and Related Structures (Atlantis Press, Paris, 2008).CrossRefGoogle Scholar
Basile, D. and Bella, A., ‘About remainders in compactifications of homogeneous spaces’, Comment. Math. Univ. Carolin. 50 (4) (2009), 607–613.Google Scholar
Borges, C. R. and Wehrly, A. C., ‘A study of $D$-spaces’, Topology Proc. 16 (1991), 7–15.Google Scholar
Douwen, E. K. and Pfeffer, W. F., ‘Some properties of the Sorgenfrey line and related spaces’, Pacific J. Math. 81 (1979), 371–377.CrossRefGoogle Scholar
Engelking, R., General Topology, revised and completed edition (Heldermann Verlag, Berlin, 1989).Google Scholar
Gerlits, J., Juh’asz, I. and Szentmikl’ossy, Z., ‘Two improvements on Tkačenko’s addition theorem’, Comment. Math. Univ. Carolin. 46 (4) (2005), 705–710.Google Scholar
Gul’ko, A. S., ‘Rectifiable spaces’, Topology Appl. 68 (1996), 107–112.CrossRefGoogle Scholar
Henriksen, M. and Isbell, J., ‘Some properties of compactifications’, Duke Math. J. 25 (1958), 83–106.CrossRefGoogle Scholar
Lin, F. and Lin, S., ‘About remainders in compactifications of paratopological groups’, ArXiv: 1106.3836v1 [Math. GN] 20 June 2011.Google Scholar