Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-10T11:22:07.020Z Has data issue: false hasContentIssue false
  • English
  • Français

TIGHT UNIVERSAL TRIANGULAR FORMS

Part of: Forms and linear algebraic groups Additive number theory; partitions

Published online by Cambridge University Press:  18 November 2021

MINGYU KIM Open the ORCID record for MINGYU KIM [Opens in a new window]
MINGYU KIM*
Affiliation:
Department of Mathematics, Sungkyunkwan University, Suwon 16419, Korea
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a subset S of nonnegative integers and a vector 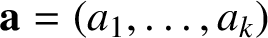$\mathbf {a}=(a_1,\ldots ,a_k)$ of positive integers, define the set 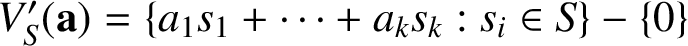$V^{\prime }_S(\mathbf {a})=\{ a_1s_1+\cdots +a_ks_k : s_i\in S\}-\{0\}$ . For a positive integer n, let 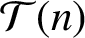$\mathcal T(n)$ be the set of integers greater than or equal to n. We consider the problem of finding all vectors 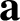$\mathbf {a}$ satisfying 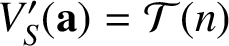$V^{\prime }_S(\mathbf {a})=\mathcal T(n)$ when S is the set of (generalised) m-gonal numbers and n is a positive integer. In particular, we completely resolve the case when S is the set of triangular numbers.

Keywords

tight universal formpolygonal number

MSC classification

Primary: 11E12: Quadratic forms over global rings and fields
Secondary: 11E20: General ternary and quaternary quadratic forms; forms of more than two variables 11P99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 3 , June 2022 , pp. 372 - 384
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by a National Research Foundation of Korea (NRF) grant funded by the government of Korea (MSIT) (NRF-2021R1C1C2010133).

References

Bhargava, M., ‘On the Conway–Schneeberger fifteen theorem’, Contemp. Math. 272 (2000), 27–38.CrossRefGoogle Scholar
Bosma, W. and Kane, B., ‘The triangular theorem of eight and representation by quadratic polynomials’, Proc. Amer. Math. Soc. 141(5) (2013), 1473–1486.CrossRefGoogle Scholar
Conway, J. H., ‘Universal quadratic forms and the fifteen theorem’, Contemp. Math. 272 (2000), 23–26.CrossRefGoogle Scholar
Ge, F. and Sun, Z.-W., ‘On some universal sums of generalized polygonal numbers’, Colloq. Math. 145 (2016), 149–155.Google Scholar
Jones, B. W., Representation by Positive Ternary Quadratic Forms (PhD Thesis, University of Chicago, 1928).Google Scholar
Ju, J., ‘Universal sums of generalized pentagonal numbers’, Ramanujan J. 51(3) (2020), 479–494.CrossRefGoogle Scholar
Ju, J. and Oh, B.-K., ‘Universal sums of generalized octagonal numbers’, J. Number Theory 190 (2018), 292–302.CrossRefGoogle Scholar
Kim, D., ‘Weighted sums of generalized polygonal numbers with coefficients 1 or 2’, Acta Arith., to appear.Google Scholar
Kim, M. and Oh, B.-K., ‘Regular ternary triangular forms’, J. Number Theory 214 (2020), 137–169.CrossRefGoogle Scholar
Kim, M. and Oh, B.-K., ‘Tight universal quadratic forms’, Preprint, arXiv:2104.02440 (2021).Google Scholar
Kitaoka, Y., Arithmetic of Quadratic Forms, Cambridge Tracts in Mathematics, 106 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
O’Meara, O. T., Introduction to Quadratic Forms (Springer, New York, 1963).CrossRefGoogle Scholar
Sun, Z.-W., ‘A result similar to Lagrange’s theorem’, J. Number Theory 162 (2016), 190–211.Google Scholar