Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-17T13:19:20.894Z Has data issue: false hasContentIssue false
  • English
  • Français

POINTS OF SMALL HEIGHT ON AFFINE VARIETIES DEFINED OVER FUNCTION FIELDS OF FINITE TRANSCENDENCE DEGREE

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  05 October 2020

DRAGOS GHIOCA Open the ORCID record for DRAGOS GHIOCA [Opens in a new window]  and
DAC-NHAN-TAM NGUYEN Open the ORCID record for DAC-NHAN-TAM NGUYEN [Opens in a new window]
DRAGOS GHIOCA*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2, Canada
DAC-NHAN-TAM NGUYEN
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a direct proof of a Bogomolov-type statement for affine varieties V defined over function fields K of finite transcendence degree over an arbitrary field k, generalising a previous result (obtained through a different approach) of the first author in the special case when K is a function field of transcendence degree 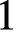$1$ . Furthermore, we obtain sharp lower bounds for the Weil height of the points in 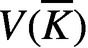$V(\overline {K})$ , which are not contained in the largest subvariety 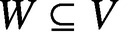$W\subseteq V$ defined over the constant field 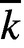$\overline {k}$ .

Keywords

function fieldsWeil heightBogomolov conjecture

MSC classification

Primary: 11G50: Heights
Secondary: 11G10: Abelian varieties of dimension $> 1$ 14G17: Positive characteristic ground fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 3 , June 2021 , pp. 418 - 427
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bilu, Y., ‘Limit distribution of small points on algebraic tori’, Duke Math. J. 89(3) (1997), 465–476.CrossRefGoogle Scholar
Bombieri, E. and Zannier, U., ‘Algebraic points on subvarieties of ${\mathbb{G}}_m^n$ ’, Int. Math. Res. Not. 7 (1995), 333–347.CrossRefGoogle Scholar
Ghioca, D., The Arithmetic of Drinfeld Modules, PhD Thesis, University of California, Berkeley, 2005.Google Scholar
Ghioca, D., ‘Points of small height on varieties defined over a function field’, Canad. Math. Bull. 52(2) (2009), 237–244.CrossRefGoogle Scholar
Ghioca, D., ‘A Bogomolov type statement for function fields’, Bull. Inst. Math. Acad. Sin. 9(4) (2014), 641–656.Google Scholar
Lang, S., Fundamentals of Diophantine Geometry (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
Serre, J.-P., Lectures on the Mordell-Weil Theorem, 3rd edn, Aspects of Mathematics, 15 (Friedrich Vieweg & Sohn, Braunschweig, 1997).CrossRefGoogle Scholar
Ullmo, E., ‘Positivité et discrétion des points algébriques des courbes’ (in French) [Positivity and discreteness of algebraic points of curves], Ann. Math. (2) 147(1) (1998), 167–179.CrossRefGoogle Scholar
Zhang, S., ‘Positive line bundles on arithmetic varieties’, J. Amer. Math. Soc. 8(1) (1995), 187–221.CrossRefGoogle Scholar
Zhang, S., ‘Equidistribution of small points on abelian varieties’, Ann. Math. (2) 147(1) (1998), 159–165.CrossRefGoogle Scholar