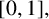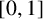Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BATES, BRUCE
BUNDER, MARTIN
and
TOGNETTI, KEITH
2022.
BINARY SIGNED-DIGIT REPRESENTATIONS IN PAPERFOLDING.
Bulletin of the Australian Mathematical Society,
Vol. 106,
Issue. 3,
p.
363.