Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T19:17:23.887Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE GENERALISATION OF SIDEL’NIKOV’S THEOREM TO 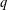$q$-ARY LINEAR CODES

Part of: Numerical mathematics Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  27 May 2019

YILUN WEI Open the ORCID record for YILUN WEI [Opens in a new window] ,
BO WU Open the ORCID record for BO WU [Opens in a new window]  and
QIJIN WANG Open the ORCID record for QIJIN WANG [Opens in a new window]
YILUN WEI
Affiliation:
School of Mathematical Sciences, Anhui University, Hefei, Anhui, 230601, China email [email protected]
BO WU
Affiliation:
School of Mathematical Sciences, Anhui University, Hefei, Anhui, 230601, China email [email protected]
QIJIN WANG*
Affiliation:
Anhui Xinhua University, Hefei, Anhui, 230088, China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalise Sidel’nikov’s theorem from binary codes to 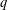$q$-ary codes for 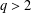$q>2$. Denoting by 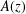$A(z)$ the cumulative distribution function attached to the weight distribution of the code and by 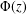$\unicode[STIX]{x1D6F7}(z)$ the standard normal distribution function, we show that 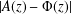$|A(z)-\unicode[STIX]{x1D6F7}(z)|$ is bounded above by a term which tends to 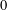$0$ when the code length tends to infinity.

Keywords

q-ary linear codeestimationSidel’nikov’s theorem

MSC classification

Primary: 94B05: Linear codes, general
Secondary: 97N20: Rounding, estimation, theory of errors
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 157 - 162
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author (corresponding author) is supported by Key Project of Natural Science Research of Anhui Higher Education Institutions (K J2018A0589).

References

Delsarte, P., ‘Distance distribution of functions over Hamming spaces’, Philips Res. Rep. 30 (1975), 1–8.Google Scholar
Esseen, C. G., ‘On the remainder term in the central limit theorem’, Ark. Mat. 8 (1969), 7–15.Google Scholar
Huffman, W. C. and Pless, V., Fundamentals of Error-Correcting Code (Cambridge University Press, Cambridge, 2003).Google Scholar
MacWilliams, F. J. and Sloane, N. J. A., The Theory of Error-Correcting Codes. I, North-Holland Mathematical Library, 16 (North-Holland, Amsterdam, 1977).Google Scholar
Shi, M. J., Rioul, O. and Solé, P., ‘On the asymptotic normality of $Q$ -ary linear codes’, in preparation.Google Scholar
Shi, M. J., Qian, L. Q., Sok, L., Aydin, N. and Solé, P., ‘On constacyclic codes over ℤ4[u]/〈u 2 - 1〉 and their Gray images’, Finite Fields Appl. 45 (2017), 86–95.Google Scholar
Shi, M. J., Sepasdar, Z., Alahmadi, A. and Solé, P., ‘On two weight ℤ2 k -codes’, Des. Codes Cryptogr. 86 (2018), 1201–1209.Google Scholar
Shi, M. J., Wu, R. S., Qian, L. Q., Sok, L. and Solé, P., ‘New classes of p-ary few weight codes’, Bull. Malays. Math. Sci. Soc., to appear.Google Scholar
Shi, M. J. and Zhang, Y. P., ‘Quasi-twisted codes with constacyclic constituent codes’, Finite Fields Appl. 39 (2016), 159–178.Google Scholar
Shi, M. J., Zhu, H. W. and Solé, P., ‘How many weights can a linear code have?’, Des. Codes Cryptogr. 87 (2019), 87–95.Google Scholar