Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T04:17:56.036Z Has data issue: false hasContentIssue false
  • English
  • Français

MANY FINITE-DIMENSIONAL LIFTING BUNDLE GERBES ARE TORSION

Part of: Global differential geometry

Published online by Cambridge University Press:  17 September 2021

DAVID MICHAEL ROBERTS Open the ORCID record for DAVID MICHAEL ROBERTS [Opens in a new window]
DAVID MICHAEL ROBERTS*
Affiliation:
School of Mathematical Sciences, The University of Adelaide, Adelaide, SA5005, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Many bundle gerbes are either infinite-dimensional, or finite-dimensional but built using submersions that are far from being fibre bundles. Murray and Stevenson [‘A note on bundle gerbes and infinite-dimensionality’, J. Aust. Math. Soc.90(1) (2011), 81–92] proved that gerbes on simply-connected manifolds, built from finite-dimensional fibre bundles with connected fibres, always have a torsion 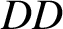$DD$ -class. I prove an analogous result for a wide class of gerbes built from principal bundles, relaxing the requirements on the fundamental group of the base and the connected components of the fibre, allowing both to be nontrivial. This has consequences for possible models for basic gerbes, the classification of crossed modules of finite-dimensional Lie groups, the coefficient Lie-2-algebras for higher gauge theory on principal 2-bundles and finite-dimensional twists of topological K-theory.

Keywords

bundle gerbestorsion classescentral extensions

MSC classification

Primary: 53C08: Gerbes, differential characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 2 , April 2022 , pp. 323 - 338
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the Australian Research Council’s Discovery Projects funding scheme (grant number DP180100383), funded by the Australian Government.

References

Becker, K. E., Murray, M. K. and Stevenson, D., ‘The Weyl map and bundle gerbes’, J. Geom. Phys. 149 (2020), Article ID 103572, 19 pages.CrossRefGoogle Scholar
Borel, A., ‘Sur la cohomologie des espaces fibrés principaux et des espaces homogènes de groupes de Lie compacts’, Ann. of Math. (2) 57 (1953), 115–207.CrossRefGoogle Scholar
Brylinski, J.-L., Loop Spaces, Characteristic Classes and Geometric Quantisation, Progress in Mathematics, 107 (Birkhäuser, Boston, MA, 1993).CrossRefGoogle Scholar
Carey, A., Johnson, S., Murray, M. K., Stevenson, D. and Wang, B.-L., ‘Bundle gerbes for Chern–Simons and Wess–Zumino–Witten theories’, Comm. Math. Phys. 259 (2005), 577–613.10.1007/s00220-005-1376-8CrossRefGoogle Scholar
Cartan, H. and Eilenberg, S., Homological Algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Feshbach, M., ‘The image of ${H}^{\ast}\left(\mathrm{BG},\mathbb{Z}\right)$ in ${H}^{\ast}\left(\mathrm{BT},\mathbb{Z}\right)$ for $G$ a compact Lie group with maximal torus $T$ ’, Topology 20(1) (1981), 93–95.CrossRefGoogle Scholar
Gawȩdzki, K. and Reis, N., ‘Basic gerbe over non-simply connected compact groups’, J. Geom. Phys. 50(1–4) (2004), 28–55.CrossRefGoogle Scholar
Gawȩdzki, K. and Waldorf, K., ‘Polyakov–Wiegmann formula and multiplicative gerbes’, J. High Energy Phys. 9 (2009), Article ID 073, 31 pages.Google Scholar
Grothendieck, A., ‘Le groupe de Brauer I’, in Dix Exposés sur la Cohomologie des Schémas (eds. Giraud, J., Grothendieck, A., Kleiman, L., Raynaud, M. and Tate, J.) (North-Holland, Amsterdam, 1968), 46–66.Google Scholar
Henriques, A., ‘The classification of chiral WZW models by ${H}_{+}^4\left(\mathrm{BG},\mathbb{Z}\right)$ ’, in Lie Algebras, Vertex Operator Algebras, and Related Topics (eds. Barron, K., Jurisich, E., Milas, A. and Misra, K.), Contemporary Mathematics, 695 (American Mathematical Society, Providence, RI, 2017), 99–122.10.1090/conm/695/13998CrossRefGoogle Scholar
Johnson, S., Constructions with Bundle Gerbes (PhD Thesis, University of Adelaide, 2003).Google Scholar
Krepski, D., ‘Basic equivariant gerbes on non-simply connected compact simple Lie groups’, J. Geom. Phys. 133 (2018), 30–41.CrossRefGoogle Scholar
Murray, M. K., ‘Bundle gerbes’, J. Lond. Math. Soc. 54(2) (1996), 403–416.10.1112/jlms/54.2.403CrossRefGoogle Scholar
Murray, M. K. and Stevenson, D., ‘Bundle gerbes: stable isomorphism and local theory’, J. Lond. Math. Soc. (2) 62(3) (2000), 925–937.CrossRefGoogle Scholar
Murray, M. K. and Stevenson, D., ‘A note on bundle gerbes and infinite-dimensionality’, J. Aust. Math. Soc. 90(1) (2011), 81–92.CrossRefGoogle Scholar
Ramzi, M., ‘A note on the universal coefficient theorem with twisted coefficients’, unpublished notes, 2021, https://sites.google.com/view/maxime-ramzi-en/notes/twisted-uct.Google Scholar
Randal-Williams, O., ‘Exercise in Spanier to get universal coefficient theorem for cohomology with local coefficients’, Mathematics Stack Exchange, https://math.stackexchange.com/q/4135432 (version: 2021-05-11).Google Scholar
Schommer-Pries, C. J., ‘Central extensions of smooth 2-groups and a finite-dimensional string 2-group’, Geom. Topol. 15(2) (2011), 609–676.CrossRefGoogle Scholar
Spanier, E. H., Algebraic Topology (McGraw-Hill, New York, 1966).Google Scholar
Waldorf, K., ‘A global perspective to connections on principal 2-bundles’, Forum Math. 30(4) (2018), 809–843.10.1515/forum-2017-0097CrossRefGoogle Scholar