Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-19T03:25:00.408Z Has data issue: false hasContentIssue false
  • English
  • Français

USING ALMOST-EVERYWHERE THEOREMS FROM ANALYSIS TO STUDY RANDOMNESS

Published online by Cambridge University Press:  10 October 2016

KENSHI MIYABE ,
ANDRÉ NIES  and
JING ZHANG
KENSHI MIYABE
Affiliation:
DEPARTMENT OF MATHEMATICS SCHOOL OF SCIENCE AND TECHNOLOGY MEIJI UNIVERSITY, JAPAN E-mail: [email protected]
ANDRÉ NIES
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF AUCKLAND, NEW ZEALAND E-mail: [email protected]
JING ZHANG
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES CARNEGIE MELLON UNIVERSITY, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study algorithmic randomness notions via effective versions of almost-everywhere theorems from analysis and ergodic theory. The effectivization is in terms of objects described by a computably enumerable set, such as lower semicomputable functions. The corresponding randomness notions are slightly stronger than Martin–Löf (ML) randomness.

We establish several equivalences. Given a ML-random real z, the additional randomness strengths needed for the following are equivalent.

  1. (1) all effectively closed classes containing z have density 1 at z.

  2. (2) all nondecreasing functions with uniformly left-c.e. increments are differentiable at z.

  3. (3) z is a Lebesgue point of each lower semicomputable integrable function.

We also consider convergence of left-c.e. martingales, and convergence in the sense of Birkhoff’s pointwise ergodic theorem. Lastly, we study randomness notions related to density of 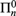${\rm{\Pi }}_n^0$ and 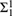${\rm{\Sigma }}_1^1$ classes at a real.

Keywords

Lebesgue densityrandomnessergodic theoryalmost-everywhere theorem
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 22 , Issue 3 , September 2016 , pp. 305 - 331
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bienvenu, L., Day, A., Greenberg, N., Kučera, A., Miller, J., Nies, A., and Turetsky, D., Computing K-trivial sets by incomplete random sets, this Bulletin, vol. 20 (2014), pp. 80–90.Google Scholar
Bienvenu, L., Day, A. R., Hoyrup, M., Mezhirov, I., and Shen, A., A constructive version of Birkhoff’s ergodic theorem for Martin-Löf random points . Information and Computation, vol. 210 (2012), pp. 21–30.Google Scholar
[3] Bienvenu, L., Greenberg, N., Kučera, A., Nies, A., and Turetsky, D., Coherent randomness tests and computing the K-trivial sets. Journal of the European Mathematical Society , 2015, to appear.Google Scholar
Bienvenu, L., Hölzl, R., Miller, J., and Nies, A., Denjoy, Demuth, and Density . Journal of Mathematical Logic, 1450004, 2014, 35 p.Google Scholar
Birkhoff, G., The mean ergodic theorem . Duke Mathematical Journal, vol. 5 (1939), no. 1, pp. 19–20.Google Scholar
Bogachev, V. I., Measure Theory, vol. I, II, Springer-Verlag, Berlin, 2007.CrossRefGoogle Scholar
Brattka, V., Miller, J., and Nies, A., Randomness and differentiability . Transactions of the AMS, vol. 368 (2016), pp. 581–605. ArXiv version at http://arxiv.org/abs/1104.4465.Google Scholar
Carothers, N. L., Real Analysis, Cambridge University Press, Cambridge, 2000.Google Scholar
Day, A. R. and Miller, J. S., Cupping with random sets . Proceedings of the American Mathematical Society, vol. 142 (2014), no. 8, pp. 2871–2879.Google Scholar
Day, A. R. and Miller, J. S., Density, forcing and the covering problem . Mathematical Research Letters, vol. 22 (2015), no. 3, pp. 719–727.Google Scholar
Demuth, O., The differentiability of constructive functions of weakly bounded variation on pseudo numbers . Commentationes Mathematicae Universitatis Carolinae, vol. 16 (1975), no. 3, pp. 583–599 (In Russian).Google Scholar
Downey, R. and Hirschfeldt, D., Algorithmic Randomness and Complexity, Springer-Verlag, Berlin, 2010, 855 p.Google Scholar
[13] Downey, R., Nies, A., Weber, R., and Yu, L., Lowness and ${\rm{\Pi }}_2^0$ nullsets, this Journal, vol. 71 (2006), no. 3, pp. 1044–1052.Google Scholar
Durrett, R., Probability: Theory and Examples, second ed., Duxbury Press, Belmont, CA, 1996.Google Scholar
Figueira, S., Hirschfeldt, D., Miller, J., Ng, Selwyn, and Nies, A, Counting the changes of random ${\rm{\Delta }}_2^0$ sets . Journal of Logic and Computation, vol. 25 (2015), pp. 1073–1089. Journal version of conference paper at CiE 2010.Google Scholar
Franklin, J., Greenberg, N., Miller, J. S., and Ng, K. M., Martin-Löf random points satisfy Birkhoff’s ergodic theorem for effectively closed sets . Proceedings of the American Mathematical Society, vol. 140 (2012), no. 10, pp. 3623–3628.Google Scholar
Franklin, J. and Towsner, H., Randomness and non-ergodic systems . Moscow Mathematical Journal, vol. 14 (2014), pp. 711–714.Google Scholar
Freer, C., Kjos-Hanssen, B., Nies, A., and Stephan, F., Algorithmic aspects of lipschitz functions . Computability, vol. 3 (2014), no. 1, pp. 45–61.Google Scholar
Gács, P., Hoyrup, M., and Rojas, C., Randomness on computable probability spaces - a dynamical point of view . Theory of Computing Systems, vol. 48 (2011), no. 3, 465–485.Google Scholar
Hoyrup, M. and Rojas, C., Computability of probability measures and Martin-Löf randomness over metric spaces . Information and Computation, vol. 207 (2009), no. 7, pp. 830–847.Google Scholar
Kautz, S., Degrees of Random Sets, Ph.D. dissertation, Cornell University, Ithaca, NY, 1991.Google Scholar
Khan, M., Lebesgue density and ${\rm{\Pi }}_1^0$ -classes. Journal of Symbolic Logic , to appear.Google Scholar
Krengel, U., Ergodic Theorems, W. de Gruyter, Boston, 1985.Google Scholar
Kurtz, S., Randomness and genericity in the degrees of unsolvability, Ph.D. dissertation, University of Illinois, Urbana, 1981.Google Scholar
Lebesgue, H., Leçons sur l’Intégration et la recherche des fonctions primitives . Gauthier-Villars, Paris, 1904.Google Scholar
Lebesgue, H., Sur les intégrales singulières . Annales de la Faculte des Sciences de Toulouse sciences Mathematics Science Physics (3), vol. 1 (1909), pp. 25–117.Google Scholar
Lebesgue, H., Sur l’intégration des fonctions discontinues . Annales scientifiques de l’ Ecole normale supérieure, vol. 27 (1910), pp. 361–450.Google Scholar
Li, M. and Vitányi, P., An Introduction to Kolmogorov Complexity and its Applications, second ed., Graduate Texts in Computer Science, Springer-Verlag, New York, 1997.CrossRefGoogle Scholar
Miller, J. S., Lebesgue density in ${\rm{\Pi }}_1^0$ -classes. Slides, Available at http://www-2.dc.uba.ar/ccr/talks/miller0201.pdf, February 2013.Google Scholar
[30] Miller, J. S. and Nies, A., Randomness and computability: Open questions, this Bulletin, vol. 12 (2006), no. 3, pp. 390–410.Google Scholar
Miyabe, K., Characterization of Kurtz randomness by a differentiation theorem . Theory of Computing Systems, vol. 52 (2013), no. 1, pp. 113–132.Google Scholar
Morayne, M. and Solecki, S., Martingale proof of the existence of Lebesgue points . Real Analysis Exchange, vol. 15 (1989/90), no. 1, pp. 401–406.Google Scholar
Nies, A., Computability and Randomness , Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009, 444 p. Paperback version 2011.Google Scholar
Nies, A., Differentiability of polynomial time computable functions , 31st International Symposium on Theoretical Aspects of Computer Science (STACS 2014) (Mayr, E. W. and Portier, N., editors), Leibniz International Proceedings in Informatics (LIPIcs), vol. 25, Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany, 2014, pp. 602–613.Google Scholar
Pathak, N., Rojas, C., and Simpson, S. G., Schnorr randomness and the Lebesgue differentiation theorem . Proceedings of the American Mathematical Society, vol. 142 (2014), no. 1, pp. 335–349.Google Scholar
Pour-El, M. and Richards, J., Computability in Analysis and Physics, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1989.Google Scholar
Rudin, W., Real and Complex Analysis, third ed., McGraw-Hill, New York, 1987.Google Scholar
Schnorr, C. P., Zufälligkeit und Wahrscheinlichkeit , Eine algorithmische Begründung der Wahrscheinlichkeitstheorie, vol. 218, Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1971.Google Scholar
V’yugin, V., Ergodic theorems for individual random sequences . Theoretical Computer Science, vol. 207 (1998), no. 2, pp. 343–361.Google Scholar
Weihrauch, K., Computable Analysis, Springer, Berlin, 2000.Google Scholar