On New Notions of Algorithmic Dimension, Immunity, and Medvedev Degree

Abstract

We prove various results connected together by the common thread of computability theory.

First, we investigate a new notion of algorithmic dimension, the inescapable dimension, which lies between the effective Hausdorff and packing dimensions. We also study its generalizations, obtaining an embedding of the Turing degrees into notions of dimension.

We then investigate a new notion of computability theoretic immunity that arose in the course of the previous study, that of a set of natural numbers with no co-enumerable subsets. We demonstrate how this notion of 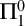$\Pi ^0_1$ -immunity is connected to other immunity notions, and construct $\Pi ^0_1$ -immune reals throughout the high/low and Ershov hierarchies. 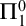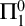We also study those degrees that cannot compute or cannot co-enumerate a $\Pi ^0_1$ -immune set.

Finally, we discuss a recently discovered truth-table reduction for transforming a Kolmogorov–Loveland random input into a Martin-Löf random output by exploiting the fact that at least one half of such a KL-random is itself ML-random. We show that there is no better algorithm relying on this fact, in the sense that there is no positive, linear, or bounded truth-table reduction which does this. We also generalize these results to the problem of outputting randomness from infinitely many inputs, only some of which are random.

Abstract prepared by David J. Webb.

E-mail: [email protected]

URL: https://arxiv.org/pdf/2209.05659.pdf