Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T19:19:42.371Z Has data issue: false hasContentIssue false
  • English
  • Français

NONMEASURABLE SETS AND UNIONS WITH RESPECT TO TREE IDEALS

Part of: Classical measure theory Set theory

Published online by Cambridge University Press:  19 June 2020

MARCIN MICHALSKI ,
ROBERT RAŁOWSKI  and
SZYMON ŻEBERSKI
MARCIN MICHALSKI
Affiliation:
DEPARTMENT OF FUNDAMENTALS OF COMPUTER SCIENCE FACULTY OF FUNDAMENTAL PROBLEMS OF TECHNOLOGY WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY WYBRZEŻE WYSPIAŃSKIEGO 27, 50-370 WROCŁAW, POLAND E-mail: [email protected] E-mail: [email protected] E-mail: [email protected]
ROBERT RAŁOWSKI
Affiliation:
DEPARTMENT OF FUNDAMENTALS OF COMPUTER SCIENCE FACULTY OF FUNDAMENTAL PROBLEMS OF TECHNOLOGY WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY WYBRZEŻE WYSPIAŃSKIEGO 27, 50-370 WROCŁAW, POLAND E-mail: [email protected] E-mail: [email protected] E-mail: [email protected]
SZYMON ŻEBERSKI
Affiliation:
DEPARTMENT OF FUNDAMENTALS OF COMPUTER SCIENCE FACULTY OF FUNDAMENTAL PROBLEMS OF TECHNOLOGY WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY WYBRZEŻE WYSPIAŃSKIEGO 27, 50-370 WROCŁAW, POLAND E-mail: [email protected] E-mail: [email protected] E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

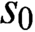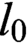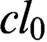In this paper, we consider a notion of nonmeasurablity with respect to Marczewski and Marczewski-like tree ideals $s_0$ , $m_0$ , $l_0$ , $cl_0$ , 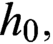$h_0,$ and 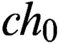$ch_0$ . We show that there exists a subset of the Baire space 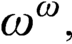$\omega ^\omega ,$ which is s-, l-, and m-nonmeasurable that forms a dominating m.e.d. family. We investigate a notion of 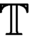${\mathbb {T}}$ -Bernstein sets—sets which intersect but do not contain any body of any tree from a given family of trees ${\mathbb {T}}$ . We also obtain a result on 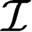${\mathcal {I}}$ -Luzin sets, namely, we prove that if ${\mathfrak {c}}$ is a regular cardinal, then the algebraic sum (considered on the real line ${\mathbb {R}}$ ) of a generalized Luzin set and a generalized Sierpiński set belongs to 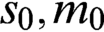$s_0, m_0$ , 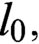$l_0,$ and 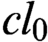$cl_0$ .

Keywords

Marczewski idealperfect treeLaver treeMiller treeHechler treeBernstein setm.e.d. familydominating familynonmeasurable setPolish spaceContinuum Hypothesistree idealI-Luzin set

MSC classification

Primary: 03E17: Cardinal characteristics of the continuum 03E50: Continuum hypothesis and Martin's axiom 03E75: Applications of set theory
Secondary: 28A99: None of the above, but in this section
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 26 , Issue 1 , March 2020 , pp. 1 - 14
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Brendle, J., Strolling trough paradise . Fundamenta Mathematicae , vol. 148 (1995), pp. 1–25.CrossRefGoogle Scholar
Kechris, A., Classical Descriptive Set Theory , Springer, New York, 2019.Google Scholar
Kunen, K., Set Theory. An Introduction to Independence Proofs , North-Holland, Amsterdam, 1980.Google Scholar
Marczewski (Szpilrajn), E., Remarques sur les fonctions complètement additives d’ensemble et sur les ensembles jouissant de la propriété de Baire . Fundamenta Mathematicae , vol. 22 (1934), pp. 303–311.Google Scholar
Marczewski (Szpilrajn), E., Sur une classe de fonctions de W. Sierpiński et la classe correspondante d’ensembles . Fundamenta Mathematicae , vol. 24 (1935), pp. 17–34.Google Scholar
Michalski, M. and Żeberski, Sz., Some properties of I-luzin . Topology and its Applications , vol. 189 (2015), pp. 122–135.CrossRefGoogle Scholar
Miller, A. W., Hechler and Laver trees. Preprint, 2012, arXiv:1204.5198.Google Scholar
Rałowski, R., Families of sets with nonmeasurable unions with respect to ideals defined by trees . Archive for Mathematical Logic , vol. 54 (2015), pp. 649–658.CrossRefGoogle Scholar
Rałowski, R., Dominating m.a.d. families in Baire space. RIMS Kôkyûroku No. 1949 , 2015, pp. 73–80.Google Scholar
Repický, M., Perfect sets and collapsing continuum . Commentationes Mathematicae Universitatis Carolinae , vol. 44 (2003), pp. 315–327.Google Scholar
Rothberger, F., Eine Äquivalenz zwischen der Kontinuumhypothese und der Existenz der Lusinschen und Sierpińskischen Mengen . Fundamenta Mathematicae , vol. 30 (1938), pp. 215–217.CrossRefGoogle Scholar
Shelah, S., Judah, H., and Miller, A., Sacks forcing, Laver forcing and Martin’s axiom . Archive for Mathematical Logic , vol. 31 (1992), pp. 145–161.Google Scholar
Shelah, S., Spinas, O., Goldstern, M., and Repický, M., On tree ideals . Proceedings of the American Mathematical Society , vol. 123 (1995), pp. 1573–1581.Google Scholar
Jech, T., Set Theory , millennium ed, Springer-Verlag, Berlin, 2003.Google Scholar
Weiss, T. and Kysiak, M., Small subsets of the reals and tree forcing notions . Proceedings of the American Mathematical Society , vol. 132 (2003), pp. 251–259.Google Scholar
Wohofsky, W., Brendle, J., and Khomskii, Y., Cofinalities of Marczewski-like ideals . Colloquium Mathematicum , vol. 150 (2017), pp. 1–10.Google Scholar