MENAS’S CONJECTURE REVISITED

Abstract

In an article published in 1974, Menas conjectured that any stationary subset of 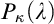can be split in 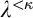many pairwise disjoint stationary subsets. Even though the conjecture was shown long ago by Baumgartner and Taylor to be consistently false, it is still haunting papers on 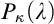. In which situations does it hold? How much of it can be proven in ZFC? We start with an abridged history of the conjecture, then we formulate a new version of it, and finally we keep weakening this new assertion until, building on the work of Usuba, we hit something we can prove.

1 The original conjecture

Throughout the paper $\kappa $ will denote a regular uncountable cardinal, and a cardinal greater than $\kappa $ . We let denote the collection of all subsets of of size less than $\kappa $ , and the noncofinal ideal on . An ideal J on is fine if . For further definitions see the end of this section.

According to Jech [18, p. 409], one of the key concepts in the theory of large cardinals is saturation of ideals. The starting point of our story is Solovay’s seminal result [58] that for any value of $\kappa $ , the nonstationary ideal on $\kappa $ is nowhere weakly $\kappa $ -saturated. There are no large cardinals involved, so how does this fit with Jech’s statement? The first remark to make is that the proof of Solovay’s result needs choice. In fact, by another result of Solovay, under the Axiom of Determinacy, the nonstationary ideal on $\omega _1$ is prime (i.e., weakly $2$ -saturated). Returning to ZFC, we have Solovay’s result at one end, and measurable cardinals with their normal measures at the other. And in between? For each cardinal $\rho $ between $2$ and $\kappa $ , set-theorists carefully determined the exact consistency strength of $\kappa $ carrying a (normal or at least) $\kappa $ -complete, weakly $\rho $ -saturated ideal.

In the glorious early days of the study of (which was seen as a two-cardinal generalization of $\kappa $ ), it was systematically attempted to establish versions of known results on $\kappa $ (see, for instance, the problems listed in Section 0 of [24]). Failures were no problem, since they were seen as productive. By analyzing what went wrong in the attempted generalization, one acquired a better understanding of and its specificity (for example, see the work of Solovay, Menas [47], and Kunen and Pelletier [24] on normal measures on without the partition property). Thus Menas [46] boldly conjectured that holds for any possible values of $\kappa $ and , where asserts that the nonstationary ideal on is nowhere weakly -saturated.

Progress on this two-cardinal version of Solovay’s splitting result was initially slow. As observed by Kanamori in [21], most results were about with replaced by . For example, an early result of Jech [17] stated that if $\kappa $ is a successor and regular, then is nowhere weakly -saturated. This was later improved by Baumgartner who proved that for any possible values of $\kappa $ and , is nowhere weakly -saturated.

The conjecture was finally refuted by Baumgartner and Taylor [3] who showed the consistency of the failure of $MC_1 (\omega _1, \omega _2)$ . Their result can be revisited as follows. We put ( $=$ the least size of any subset of ) not in ).

Observation 1.1. If , then fails.

Proof By a result of Shelah [49], . Thus there is a stationary subset S of of size . Obviously, S can be partitioned into no more than stationary subsets.

Corollary 1.2. Suppose that and . Then fails.

Proof If , then (see, e.g., [50, p. 86]).

The conjecture somehow survived its refutation by Baumgartner and Taylor, as the so-called splitting problem, the general problem of computing the degree of weak saturation of ideals on . In how many stationary pieces can this or that stationary subset of be partitioned? Given a cardinal , what is the consistency strength of the existence of a (normal or maybe just) $\kappa $ -complete, weakly $\rho $ -saturated, fine ideal on ?

Recall that for a fine ideal J on , Jensen’s diamond principle asserts the existence of $s_x$ for such that $Z_B = \{x : B \cap x = s_x \}$ lies in $J^+$ for all . Since $\{x \in Z_a : a \subseteq x\} \cap \{x \in Z_b : b \subseteq x\} = \emptyset $ for any two distinct members $a, b$ of , implies that J is not weakly -saturated. In [43] Matsubara established the consistency of the conjecture by proving that it holds in L. As observed by Shioya [56], one way to proceed would have been to appeal to the fact that in L, ( and hence) holds for all . Instead, Matsubara relied on the result of Baumgartner in the case when , and completed his proof by showing that follows from . A new proof of this result can be found in [45]. Let us recall that an ideal J on is precipitous if for all generic , the ultrapower is well-founded. By a result of Foreman [10], any countably complete -saturated ideal on is precipitous. As is well-known, any normal, fine, weakly -saturated ideal on is -saturated (in fact -saturated) and hence precipitous. In [45] Matsubara and Shioya establish that no countably complete ideal J on with $cof (J) = non (J)$ is precipitous. It follows that if , then no restriction of is precipitous (and hence holds). Let us observe that by pushing the counting argument used in [43], one obtains the following.

Observation 1.3. Let J be a fine ideal on such that the least size of any C in $J^{\ast }$ . Then holds.

Proof Select a bijection . Let be a one-to-one enumeration of , and pick $C_i \in J^{\ast }$ for such that . Inductively construct and for as follows. Suppose that $a_r$ and $t_{a_r}$ have already been constructed for each $r < k$ . Let $k = F (i, j)$ . Now select $a_k$ in $C_i \setminus \{a_r : r < k \}$ , and put $t_{a_k} = A_j$ . Clearly, for any , (and hence ) lies in $J^+$ .

Since (see [40] for the exact value of ), it follows that if , then ( holds for every , and hence) holds.

If is a strong limit cardinal with , then , so Matsubara’s result shows that for any value of $\kappa $ , there are always many values of (of cofinality less than $\kappa $ ) for which holds. Further, Matsubara and Shelah [44] (see also [41]) have shown that if is a strong limit cardinal with , then no restriction of is precipitous (and hence holds). To sum up the results of this section, may consistently fail. On the other hand, we have the following.

Fact 1.4. Assuming GCH, the following hold:

1. (i) Suppose that either $\kappa $ is a successor cardinal, or is singular. Then holds.

2. (ii) Suppose that $\kappa $ is weakly inaccessible, is regular, and . Then holds.

A large cardinal is needed to obtain situations when [8] (see also [21, p. 345]). Thus Fact 1.4 shows that if GCH holds and there are no large cardinals in an inner model, then holds. However the large cardinals in question are of a modest size, since Donder, Koepke, and Levinski [8] showed that if and is $\kappa $ -Erdős, then the set is stationary. We can do better than this. Recall that any normal, fine, weakly -saturated ideal on is precipitous. Hence if GCH holds, $\kappa $ is weakly inaccessible, , and there is no normal, precipitous, fine ideal on , then no normal, fine ideal on is weakly -saturated. Now if carries a precipitous ideal, then by a result of Magidor (see [43]), there is a cardinal $\sigma $ of Mitchell order $\sigma ^{++}$ in some inner model. Thus the following formulation seems preferable.

Fact 1.5. Assuming GCH, the following hold:

1. (i) Suppose that either $\kappa $ is a successor cardinal, or is singular. Then holds.

2. (ii) Suppose that $\kappa $ is weakly inaccessible, is regular, and carries no precipitous ideal. Then holds.

This discussion is continued in Section 9 where we show that if there are no large cardinals in an inner model, then Menas’s conjecture is equivalent to a weak form of GCH.

Let us at last provide the missing definitions. By an ideal on an infinite set X, we mean a nonempty collection J of subsets of X such that (a) $X \notin J$ , (b) $P(A)\subseteq J$ for all $A \in J$ , (c) $A \cup B \in J$ whenever $A, B \in J$ , and (d) $\{x\} \in J$ for all $x \in X$ . Given an ideal J on X, we let $J^+ = P(X) \setminus J$ , $J^{\ast } = \{ A \subseteq X : X \setminus A \in J\}$ , and $J \vert A = \{ B \subseteq X : B \cap A\in J\}$ for each $A \in J^+$ . For a cardinal $\rho ,J$ is $\rho $ -complete if $\bigcup Q \in J$ for every $Q \subseteq J$ with $\vert Q \vert < \rho $ . We let $non (J) =$ the least size of a set in $J^+$ . $cof (J)$ denotes the least cardinality of any $Q \subseteq J$ such that $J = \bigcup _{A \in Q} P(A)$ . Given an infinite set Y and $f : X \rightarrow Y$ , we let $f (J) = \{ B \subseteq Y : f^{-1} (B) \in J\}$ . For a cardinal $\sigma $ , J is weakly $\sigma $ -saturated (respectively, $\sigma $ -saturated) if there is no $Q \subseteq J^+$ with $\vert Q \vert = \sigma $ such that $A \cap B = \emptyset $ (respectively, $A \cap B \in J$ ) for any two distinct members $A, B$ of Q. J is nowhere weakly $\sigma $ -saturated if for any $A \in J^+$ , $J \vert A$ is not weakly $\sigma $ -saturated.

Fact 1.6.

1. (i) (Folklore) Suppose that $\sigma $ is singular, and J is nowhere weakly $\tau $ -saturated for every cardinal $\tau < \sigma $ . Then J is nowhere weakly $\sigma $ -saturated.

2. (ii) [40, (proof of) Proposition 2.6] Letting $\chi = \min \{\vert C \vert : C \in J^{\ast }\}$ , suppose that . Then $\chi =$ the largest cardinal $\tau $ such that J is not weakly $\tau $ -saturated.

3. (iii) J is weakly $\sigma $ -saturated if and only if for every $A \in J^+$ , $J \vert A$ is weakly $\sigma $ -saturated.

For a regular uncountable cardinal $\tau $ , $I_{\tau }$ (respectively, $NS_{\tau }$ ) denotes the noncofinal (respectively, nonstationary) ideal on $\tau $ . For each regular cardinal $\mu < \tau $ , $E^{\tau }_{\mu }$ , (respectively, $E^{\tau }_{< \mu }$ ) denotes the set of all infinite limit ordinals $\alpha < \tau $ such that $\mathrm {cf}(\alpha ) = \mu $ (respectively, $\mathrm {cf}(\alpha ) < \mu $ ).

2 Second and third versions of the conjecture

In view of the Baumgartner–Taylor result, it is tempting to repair the conjecture by replacing with the (weaker) assertion that is nowhere weakly -saturated (notice that since , and are equivalent for ). This would be more in line with Solovay’s result, which after all does not assert that $NS_{\kappa }$ is nowhere $\kappa ^{<\kappa }$ -saturated (this holds if and only if $2^{<\kappa } = \kappa $ ), but only that it is nowhere $cof (I_{\kappa })$ -saturated. However, Gitik [12] proved that it is consistent relative to a large cardinal that “ $\kappa $ is inaccessible and $NS_{\kappa , \kappa ^+} \vert W$ is weakly $\kappa ^+$ -saturated for some W (and hence $MC_2 (\kappa , \kappa ^+)$ fails).” Krueger [23] showed that one could take $W = \{x : o.t (x) = \vert x \cap \kappa \vert ^+ \}$ , and Shioya [56] obtained a new proof of Gitik’s result starting from the hypothesis that $\kappa $ is $\kappa ^+$ -supercompact. Magidor (see [7]) had shown that for all values of $\kappa $ and , is nowhere weakly $\kappa $ -saturated, which is thus optimal. Thus Solovay’s result that $NS_{\kappa }$ is nowhere weakly $\kappa $ -saturated does generalize, but the generalization only asserts that is nowhere weakly $\kappa $ -saturated.

Notice that if $\kappa $ is -Shelah and , then, as shown by Johnson [20], the set $W = \{x : o.t. (x) = \vert x \cap \sigma \vert ^+ \}$ lies in (and hence in ), but, by another result of Johnson [19], is not weakly -saturated. Thus the stationarity of $W = \{x : o.t. (x) = \vert x \cap \kappa \vert ^+ \}$ does not guarantee by itself that $NS_{\kappa , \kappa ^+} \vert W$ is weakly $\kappa ^+$ -saturated.

By Gitik’s result, is still too strong. One way to weaken it would be to require only that is nowhere weakly -saturated for some S. Now Usuba [60] established that if , then there is a stationary subset S of with the property that no normal, fine ideal J on with $S \in J^+$ is weakly -saturated. Taking our cue from this, we let assert the existence of S in such that no normal, fine ideal J on with $S \in J^+$ is weakly -saturated. Then any normal extension of will be nowhere weakly -saturated. Clearly, the larger S is, the better.

3 Pcf theory

In this section we start working on using tools of Shelah’s pcf theory.

3.1 Pseudo-Kurepa families

For two cardinals $\sigma $ and $\pi $ , asserts the existence of with $\vert X \vert = \pi $ such that $\vert X \cap P (b) \vert < \kappa $ for all . It is simple to see that ( , and hence) holds. These families can be used to strengthen the result of Baumgartner mentioned above. First the case when $\kappa $ is a successor cardinal:

Fact 3.1 [26].

Suppose that $\kappa $ is a successor cardinal and holds. Then no $\kappa $ -complete, fine ideal on is weakly $\pi $ -saturated.

Proof The proof is an easy modification of that of Baumgartner. Let J be a $\kappa $ -complete, fine ideal on . Put $\kappa = \nu ^+$ . We can assume that $\pi $ is greater than or equal to $\kappa $ (since we have seen that ( and hence) ) always holds) and (by Fact 1.6(i)) regular. Select with $\vert X \vert = \pi $ such that for all . For , pick a one-to-one function $f_b : X \cap P (b) \rightarrow \nu $ . By $\kappa $ -completeness and fineness of J, for each $x \in X$ , we may find $S_x \in J^+ \cap P (\{b : x \subseteq b\})$ and $\gamma _x < \nu $ such that $f_b (x) = \gamma _x$ for all $b \in S_x$ . There must be $\gamma < \nu $ and $W \subseteq X$ with $\vert W \vert = \pi $ such that $\gamma _x = \gamma $ for any $x \in W$ . Then clearly $S_x \cap S_y = \emptyset $ for any two distinct members $x, y$ of W.

In particular, as observed by Matsubara [42] long ago, if $\kappa $ is a successor cardinal, then no $\kappa $ -complete, fine ideal on is weakly -saturated.

We use more in the case when $\kappa $ is weakly inaccessible. Given an ideal J on and a cardinal $\tau $ with , J is $\tau $ -normal if for any $A \in J^+$ and any $f : A \rightarrow \tau $ such that $f(a) \in a$ for all $a \in A$ , there is $B \in J^+ \cap P(A)$ such that f is constant on B. Notice that -normality is the same as normality.

Fact 3.2 [28].

Suppose that $\tau $ and $\pi $ are two cardinals with and $\tau < \pi $ , and J is a $\tau $ -normal, fine ideal on . Suppose further that there is with $\vert X \vert = \pi $ such that . Then J is not weakly $\pi $ -saturated.

Note that if X is as in the statement of the fact, then $\vert X \cap P (c) \vert < \kappa $ for all (so X witnesses that holds). Further note that it follows from Fact 3.2 that if $\kappa $ is weakly inaccessible, then no $\kappa $ -normal, fine ideal J on with is weakly -saturated. Thus by combining Facts 3.1 and 3.2, we obtain the following.

Proposition 3.3. If , then holds.

Let us return to the special case of Fact 3.2 when and . If $\kappa $ is weakly inaccessible, , and J is a normal, fine, weakly -saturated ideal on , then it gives us that the set of all such that ( $\vert b \vert> \vert b \cap \tau \vert $ for every cardinal $\tau $ with , and hence) lies in $J^{\ast }$ . In the special case when for some regular cardinal $\sigma < \kappa $ , we can even conclude that , since it is simple to see that for any cardinal $\chi $ with , .

For another remark, letting C denote the set of all

such that (a) $o.t. (b)$ is an infinite limit ordinal, and (b) $b \setminus \tau \not = \emptyset $ , then clearly

, and moreover

for all $b \in C$ with

. For normal ideals there is the following related result of Usuba (see the proof of Proposition 6.1 in [59]) who proved it using generic embeddings.

Fact 3.4. Suppose that is regular, and let J be a normal, fine ideal on such that $S \in J^+$ , where S is the set of all such that ( $o.t. (b)$ is an infinite limit ordinal with) $\mathrm {cf} (o.t. (b)) < o.t. (b)$ . Then J is not weakly -saturated.

Proof For each infinite limit ordinal $\delta $ , select an increasing function $t_{\delta } : \mathrm {cf} (\delta ) \rightarrow \delta $ such that $\sup (ran (t_{\delta })) = \delta $ . For $b \in S$ , let $g_b : o.t. (b) \rightarrow b$ enumerate b in increasing order, and set $\tau _b = \mathrm {cf} (o.t. (b))$ and $\xi _b = g_b (\tau _b)$ . By normality of J, we may find $Y \in J^+ \cap P (S)$ and such that $\xi _b = \xi $ for all $b \in Y$ . For $\alpha \in b \in Y$ , put:

• • $F (\alpha , b) =$ the least $\zeta < \tau _b$ such that ;

• • $\beta ^b_{\alpha } = g_b (t_{o.t. (b)} (F (\alpha , b)))$ ;

• • $\gamma ^b_{\alpha } = g_b (F (\alpha , b))$ .

Thus $F (\alpha , b) < \tau _b$ , $\beta ^b_{\alpha } \in b$ and $\gamma ^b_{\alpha } \in b \cap \xi $ . For , there must be, by normality of J, $T_{\alpha } \in J^+ \cap P (\{b \in Y : \alpha \in b\})$ , , and $\gamma _{\alpha } < \xi $ such that for all $b \in T_{\alpha }$ , $\beta ^b_{\alpha } = \beta _{\alpha }$ and $\gamma ^b_{\alpha } = \gamma _{\alpha }$ . Since is regular, we may find and $\gamma < \xi $ such that $\gamma _{\alpha } = \gamma $ for all $\alpha \in d$ . Finally, pick with the property that $\beta _{\alpha } < \alpha '$ whenever $\alpha < \alpha '$ are in e. Given $\alpha < \alpha '$ in e, we claim that $T_{\alpha } \cap T_{\alpha '} = \emptyset $ . Suppose otherwise, and pick $b \in T_{\alpha } \cap T_{\alpha '}$ . Then $F (\alpha , b) = F (\alpha ', b)$ (since

$$ \begin{align*} g_b (F (\alpha, b)) = \gamma^b_{\alpha} = \gamma_{\alpha} = \gamma = \gamma_{\alpha'} = \gamma^b_{\alpha'} = g_b (F (\alpha', b))), \end{align*} $$

and therefore . Contradiction.

3.2 Scales

To handle the case when , we will use pcf theory scales. We will first study the effect of one specific scale on weak saturation of ideals on , which will keep us busy for a long while (up to the end of Section 5).

Let A be an infinite set of regular cardinals, and let I be an ideal on A such that $\{A \cap a : a \in A \} \subseteq I$ . We let $\prod A = \prod _{a \in A} a$ . For $f, g \in \prod A$ , we let $f <_I g$ if $\{a \in A : f (a) \geq g (a) \} \in I$ .

Let $\xi \in On$ , and be an increasing, cofinal sequence in $(\prod A, <_I)$ . For $X \subseteq \xi $ , the sequence is strongly increasing if there is $Z_{\xi } \in I$ for $\xi \in X$ such that $f_{\beta } (a) < f_{\xi } (a)$ whenever $\beta < \xi $ are in X and $a \in A \setminus (Z_{\beta } \cup Z_{\xi })$ .

An infinite limit ordinal $\delta < \xi $ is a good point for if there is a cofinal subset X of $\delta $ such that is strongly increasing.

Fact 3.5.

1. (i) [6, 29] If I is $\mathrm {cf} (\delta )$ -complete, then $\delta $ is a good point for .

2. (ii) [1, Lemma 2.7] Suppose that $\delta $ is a good point for . Then any cofinal subset e of $\delta $ has a cofinal subset X such that the sequence is strongly increasing.

Let $\pi $ be a regular cardinal greater than $\sup A$ . An increasing, cofinal sequence in $(\prod A, <_I)$ is said to be a scale for $\sup A$ of length $\pi $ . If there is such a sequence, we set $\mathrm {tcf} (\prod A / I) = \pi $ .

For a singular cardinal $\chi $ and a cardinal $\sigma $ with , the pseudopower $\mathrm {pp}_{\sigma } (\chi )$ is defined as the supremum of the set X of all cardinals $\pi $ for which one may find A and I such that:

• • A is a set of regular cardinals smaller than $\chi $ ;

• • $\sup A = \chi $ ;

• • ;

• • I is an ideal on A such that $\{A \cap a : a \in A \} \subseteq I$ ;

• • $\pi = \mathrm {tcf}( \prod A /I )$ .

The definition is robust in the sense that it will not be affected by minor modifications (such as requiring the ideal I to be prime) (see [16, p. 270]).

We let $\mathrm {pp} (\chi ) = \mathrm {pp}_{\mathrm {cf} (\chi )} (\chi )$ .

Fact 3.6 [50, Theorem 1.5, p. 50].

Let $\chi $ be a singular cardinal. Then there is a set A of regular cardinals such that $o.t. (A) = \mathrm {cf} (\chi ) < \min A, \sup A = \chi $ and $\mathrm {tcf} (\prod A/I) = \chi ^+$ , where I is the noncofinal ideal on A.

Thus $\mathrm {pp} (\chi ) \geq \chi ^+$ for any singular cardinal $\chi $ .

3.3 Large pseudo-Kurepa families from scales

Throughout the remainder of this section and Sections 4 and 5 , we let $\theta , \pi , A$ , and I be such that:

• • $\theta $ and $\pi $ are two cardinals such that and $\theta < \pi $ ;

• • A is a set of regular cardinals smaller than $\theta $ such that $\vert A \vert < \kappa $ and $\sup A = \theta $ ;

• • I is an ideal on A with $\{A \cap a : a \in A \} \subseteq I$ ;

• • $\pi = \mathrm {tcf} (\prod A /I )$ .

Further let be an increasing, cofinal sequence in $(\prod A, <_I)$ .

Let $\Phi $ denote a one-to-one onto function from $On \times On$ to $On$ such that $\Phi " (\sigma \times \sigma ) = \sigma $ for any infinite cardinal $\sigma $ . We let be defined by: $y_{\alpha }$ equals $\{\alpha \}$ if $\alpha < \theta $ , and $\{\Phi (a, f_{\alpha } (a)) : a \in A \}$ otherwise.

Observation 3.7. Let $\delta> \theta $ be a good point for $\vec f$ , and let e be a cofinal subset of $\delta $ of order-type $\mathrm {cf} (\delta )$ . Then $\vert \bigcup _{\alpha \in e} y_{\alpha } \vert = \max (\vert A \vert , \mathrm {cf} (\delta ))$ .

Proof By Fact 3.5(ii), we may find a subset X of $e \setminus \theta $ of order-type $\mathrm {cf} (\delta )$ such that the sequence is strongly increasing. Pick $Z_{\xi } \in I$ for $\xi \in X$ so that $f_{\beta } (a) < f_{\xi } (a)$ whenever $\beta < \xi $ are in X and $a \in A \setminus (Z_{\beta } \cup Z_{\xi })$ . Now select $k \in \prod _{\xi \in X} (A \setminus Z_{\xi })$ , and put $t = \{\Phi (k (\xi ), f_{\xi } (k (\xi ))) : \xi \in X \}$ . It is simple to see that $\vert t \vert = \vert X \vert = \mathrm {cf} (\delta )$ . It follows that

$$ \begin{align*} \vert \bigcup_{\alpha \in e} y_{\alpha} \vert \geq \vert \bigcup_{\alpha \in X} y_{\alpha} \vert \geq \max (\vert A \vert, \mathrm{cf} (\delta)). \end{align*} $$

On the other hand, it is readily verified that .

Fact 3.8.

1. (i) [37] There is a closed unbounded subset $C_{\vec {f}}$ of $\pi $ , consisting of infinite limit ordinals, with the property that any $\delta $ in $C_{\vec {f}}$ satisfying one of the following conditions, where $\rho $ denotes the largest limit cardinal less than or equal to $\mathrm {cf} (\delta )$ , is a good point for $\vec f$ :

   1. (a) $(\max (\rho , \vert A \vert ))^{+3} < \mathrm {cf} (\delta )$ .

   2. (b) $\rho ^{\vert A \vert } < \mathrm {cf} (\delta )$ .

   3. (c) $\vert A \vert < \mathrm {cf} (\rho )$ .

   4. (d) $\vert A \vert < \rho $ and I is $(\mathrm {cf} (\rho ))^+$ -complete.

   5. (e) and $\mathrm {pp} (\rho ) < \mathrm {cf} (\delta )$ .

2. (ii) [28] Suppose that and there is a closed unbounded subset C of $\pi $ such that every $\delta \in C$ of cofinality $\kappa $ is a good point for ${\vec f}$ . Then holds, as witnessed by $X = \{y_{\alpha } : \alpha < \pi \}$ .

Thus, for instance, ${\mathcal A}_{\omega _4,\sigma } (\omega _1, \sigma ^+)$ holds for every uncountable cardinal $\sigma $ of cofinality $\omega $ . On the other hand by a result of Todorcevic (see [28]), if , for every cardinal $\tau $ with , and , then fails.

The scale is good if there is a closed unbounded subset C of $\pi $ with the property that every infinite limit ordinal $\delta $ in C such that $\vert A \vert < \mathrm {cf} (\delta ) <\sup A$ is a good point for $\vec f$ .

If $\pi $ is the successor of a cardinal $\tau $ (possibly greater than $\sup A$ ) at which the weak square principle $\square _{\tau }^{\ast }$ holds, then [6, 31] the scale $\vec f$ is good. Let us recall that the failure of $\square _{\tau }^{\ast }$ for singular $\tau $ has, in the words of Jech [18, p. 702] (see also [5]), the consistency strength of (roughly) at least one Woodin cardinal.

3.4 The case

We have seen that if , then holds. We give a second proof of this fact now, under the extra assumption that is the length of a scale.

Lemma 3.9. Suppose that , and let be such that:

• • $\sup b \notin b$ .

• • Either $\sup b$ is a good point for ${\vec f}$ of cofinality greater than $ \vert A \vert $ , or I is $\mathrm {cf} (\sup b)$ -complete.

• • $ran (f_{\alpha }) \subseteq b$ for all $\alpha \in b$ .

Then .

Proof Set $\tau = \mathrm {cf} (\sup b)$ . Select an order type $\tau $ subset c of b with supremum $\sup b$ . Let us first suppose that $\sup b$ is a good point of ${\vec f}$ of cofinality greater than $ \vert A \vert $ . By Fact 3.5(ii), we may find $d \in [c]^{\tau }$ and $w_{\gamma } \in I$ for $\gamma \in d$ such that $f_{\beta } (a) < f_{\alpha } (a)$ whenever $\beta < \alpha $ are in d and $a \in A \setminus (w_{\beta } \cup w_{\alpha })$ . For $\alpha \in d$ , pick $a_{\alpha } \in A \setminus w_{\alpha }$ . There must be $a \in A$ and $e \in [d]^{\tau }$ such that $a_{\alpha } = a$ for all $\alpha \in e$ . Then is an increasing sequence of length $\tau $ with all its terms in $b \cap \theta $ .

Next suppose that I is $\tau $ -complete. For $\beta < \alpha $ in c, select $u_{\beta \alpha } \in I$ such that $f_{\beta } (a) < f_{\alpha } (a)$ whenever $a \in A \setminus u_{\beta \alpha }$ . For each $\gamma \in c$ , pick $a_{\gamma }$ in $A \setminus (\bigcup \{u_{\beta \alpha } : \beta < \alpha < \gamma $ and $\beta , \alpha \in c \})$ . Then is an increasing sequence of length $o.t. (c \cap \gamma )$ with all its terms in $b \cap \theta $ , so . It follows that .

Proposition 3.10. Suppose that , and J is a normal, fine ideal on such that either $S_1 \in J^+$ , or $S_2 \in J^+$ , where $S_1$ is the set of all such that $\sup b$ is a good point for ${\vec f}$ of cofinality greater than $ \vert A \vert $ , and $S_2$ the set of all such that I is $\mathrm {cf} (\sup b)$ -complete. Then J is not weakly -saturated.

Proof Let C be the set of all such that:

• • $\sup b \notin b$ ;

• • $ran (f_{\alpha }) \subseteq b$ for all $\alpha \in b$ ;

• • $b \setminus \theta \not = \emptyset $ .

Then clearly, . Hence, for $i = 1, 2$ , $C \cap S_i \in J^+$ . Moreover by Lemma 3.9, $\mathrm {cf} (o.t. (b)) < o.t. (b)$ for all $b \in C \cap S_i$ . The result is now immediate from Fact 3.4.

3.5 The isomorphism method

One way to show that an ideal J on is not weakly $\pi $ -saturated is to establish that it is isomorphic to some ideal K on $P_{\kappa } (\pi )$ that is itself not weakly $\pi $ -saturated. In this subsection we consider some situations when this can (or cannot) be done.

For $i = 1, 2$ , let $X_i$ be an infinite set, and let $K_i$ be an ideal on $X_i$ . We say that $K_1$ is isomorphic to $K_2$ if there are $W_1 \in K_1^{\ast }$ , $W_2 \in K_2^{\ast }$ , and a bijection $k : W_1 \rightarrow W_2$ such that $K_1^{\ast } = \{D \subseteq W_1 : k"D \in K_2^{\ast }\}$ .

Notice that $K_1$ is isomorphic to $K_2$ if and only if there are $W_1 \in K_1^{\ast }$ , $W_2 \in K_2^{\ast }$ , and a bijection $k : W_1 \rightarrow W_2$ such that (a) $\{k"D : D \in K_1^{\ast } \cap P (W_1)\} \subseteq K_2^{\ast }$ , and (b) $\{k^{- 1} (B) : B \in K_2^{\ast } \cap P (W_2)\} \subseteq K_1^{\ast }$ . It easily follows that $K_1$ is isomorphic to $K_2$ just in case $K_2$ is isomorphic to $K_1$ .

For a cardinal $\sigma> \kappa $ and a $\kappa $ -complete ideal G on $P_{\kappa } (\sigma )$ , $\overline {\mathrm {cof}} (G)$ denotes the least cardinality of any $Q \subseteq G$ such that for any $B \in G$ , there is $Z \in P_{\kappa } (Q)$ with $B \subseteq \bigcup Z$ .

Observation 3.11. For $i = 0, 1$ , let $\sigma _i$ be a cardinal greater than $\kappa $ , and let $K_i$ be a fine ideal on $P_{\kappa } (\sigma _i)$ . Suppose that $K_1$ is $\kappa $ -complete, and $K_1$ and $K_2$ are isomorphic. Then $K_2$ is $\kappa $ -complete, and moreover $\overline {\mathrm {cof}} (K_1) = \overline {\mathrm {cof}} (K_2)$ .

Fact 3.12 [36].

The following are equivalent:

1. (i) $f (K_1) = K_2$ for some one-to-one $f : X_1 \rightarrow X_2$ .

2. (ii) There are $W_2 \in K_2^{\ast }$ and a bijection $k : X_1 \rightarrow W_2$ such that $K_1^{\ast } = \{D \subseteq W_1 : k"D \in K_2^{\ast }\}$ .

We use the isomorphism method to give new versions of Facts 3.1 and 3.2. Let us start with the situation when $\kappa $ is a successor cardinal. There is a more informative proof of Fact 3.1 which runs as follows. For the first case, when , proceed as in the original proof. Now for the second case, suppose that $\kappa $ is a successor cardinal, J is a $\kappa $ -complete, fine ideal on , , and X is a size $\pi $ subset of with the property that $\vert X \cap P (b) \vert < \kappa $ for all . Letting be a one-to-one enumeration of X, define by $f (b) = b \cup \{\alpha : x_{\alpha } \subseteq b \}$ . Clearly, f is one-to-one, so by Fact 3.12, J and $f (J)$ are isomorphic. Since by the first case, $f (J)$ is not weakly $\pi $ -saturated, J is not weakly $\pi $ -saturated either. It is worth stressing that, as the following shows, there are situations when the condition on the existence of an X as above cannot be dispensed with.

Observation 3.13. Suppose that $\kappa $ is a successor cardinal, and some $\kappa $ -complete, fine ideal J on with is isomorphic to some fine ideal K on $P_{\kappa } (\pi )$ . Then holds.

Proof By Observation 3.11, K is $\kappa $ -complete, and moreover . By Proposition 5.7 in [39], the desired conclusion follows.

Observation 3.13 can be applied with . More interestingly, suppose that is a strong limit cardinal of cofinality less than $\kappa $ . Then by a result of Shelah [53], for some , so and moreover since is nowhere -saturated by Fact 1.6(ii), so is . Thus if GCH holds, $\kappa $ is a successor cardinal, , and fails, we cannot use the isomorphism trick to show that is not weakly saturated.

Let us now turn to the case when $\kappa $ is weakly inaccessible.

Observation 3.14. Suppose that , $\kappa $ is weakly inaccessible, $\sigma $ is a cardinal with , and J is a $\sigma $ -normal, fine ideal on . Suppose further that there exist a closed unbounded subset C of $\pi $ and $D \in J^+$ such that $\delta $ is a good point for $\vec {f}$ whenever $\delta \in C \cap E^{\pi }_{\vert b \cap \sigma \vert ^+}$ for some $b \in D$ . Then J is not weakly $\pi $ -saturated.

Proof Recall that is defined by: $y_{\alpha }$ equals $\{\alpha \}$ if $\alpha < \theta $ , and $\{\Phi (a, f_{\alpha } (a)) : a \in A \}$ otherwise. Define by

$$ \begin{align*} g (b) = (b \cap \sigma) \cup \{\alpha \in C \setminus \sigma : y_{\alpha} \subseteq b\}. \end{align*} $$

Notice that $g (b) \cap \theta = b \cap \theta $ . It follows that g is one-to-one in case .

Claim. Let $b \in D$ . Then $\vert g (b) \vert = \vert b \cap \sigma \vert $ .

Proof of the claim

Suppose otherwise. Pick a subset e of $g (b) \setminus \sigma $ of order-type $\vert b \cap \sigma \vert ^+$ , and put $\delta = \sup e$ . Then clearly, $\delta \in C \cap E^{\pi }_{\vert b \cap \sigma \vert ^+}$ , and therefore $\delta $ is a good point for $\vec {f}$ . But then by Observation 3.7,

$$ \begin{align*} \vert \bigcup_{\alpha \in e} y_{\alpha} \vert \geq \mathrm{cf} (\delta)> \vert b \cap \sigma \vert \geq \vert b \cap \theta \vert. \end{align*} $$

This is a contradiction, since $\bigcup _{\alpha \in e} y_{\alpha } \subseteq b \cap \theta $ , which completes the proof of the claim.

Set $K = g (J \vert D)$ and $Z = g" (D)$ . Then, as is readily checked, K is a $\sigma $ -normal, fine ideal on $P_{\kappa } (\pi )$ , and moreover $Z \in K^{\ast }$ . By the claim, $\vert x \vert $ = $\vert x \cap \sigma \vert $ for all $x \in Z$ , so by Fact 3.2, K is not weakly $\pi $ -saturated, and hence neither is J.

Corollary 3.15. Suppose that , $\kappa $ is weakly inaccessible, $\sigma $ is a cardinal with , and J is a weakly $\pi $ -saturated, $\sigma $ -normal, fine ideal on .Then $\Upsilon \in J^{\ast }$ , where $\Upsilon $ denotes the set of all for which there are stationarily many $\delta < \pi $ such that (a) $\delta $ is not a good point for ${\vec f}$ , and (b) $\mathrm {cf} (\delta ) = \vert b \cap \sigma \vert ^+$ .

Proof Suppose otherwise, and let . Let T be the set of all $\delta < \pi $ such that either $\delta \notin E^{\pi }_{\vert b \cap \sigma \vert ^+}$ for every $b \in D$ , or $\delta $ is a good point for $\vec {f}$ . Then $\pi \setminus T$ must be stationary. Hence we may find $\mu < \pi $ , and a stationary subset W of $\pi \setminus T$ , such that (a) $\mu = \vert b \cap \sigma \vert ^+$ for some $b \in D$ , and (b) $W \subseteq E^{\pi }_{\mu }$ . Notice that for any $\delta \in W$ , $\delta $ is not a good point for $\vec {f}$ . Thus $b \in \Upsilon $ . Contradiction.

The corollary extends several known results, including one by Shelah (see [9, Theorem 4.63]) asserting that above a supercompact $\chi $ , there is no good scale at any cardinal $\rho $ of cofinality smaller than $\chi $ , and a more detailed result of Sinapova [57, Lemma 8] for the special case when $\rho < \chi ^{+ \chi }$ .

4 The function $\psi $

Throughout the section it is assumed that . We need a new method to handle situations when the results established so far do not apply. In this quest the function $\psi $ considered in this section will play a key role.

Define $\varphi : P_{\theta } (\pi ) \rightarrow \prod A$ by: $\varphi (w) (a)$ equals $\sup (w \cap a)$ if $\sup (w \cap a) < a$ , and $0$ otherwise. Further define $\psi : P_{\theta } (\pi ) \rightarrow \pi $ by $\psi (w) =$ the least $\alpha $ such that .

To show that an ideal K on is not weakly $\pi $ -saturated, it will suffice to prove that the ideal on $\pi $ is (included in some ideal on $\pi $ that is) not weakly $\pi $ -saturated. As a first step, in this section we compare $\psi \vert P_{\kappa } (\pi )$ and the sup function on $P_{\kappa } (\pi )$ . The main results are Observation 4.7, which will be used in Section 5, and Observation 4.3.

A subset C of $P_{\kappa } (\pi )$ is strongly closed if $\bigcup X \in C$ for all $X \in P_{\kappa }(C) \setminus \{\emptyset \}$ . $SNS_{\kappa , \pi }$ denotes the collection of all $B \subseteq P_{\kappa }(\pi )$ such that $B \cap C = \emptyset $ for some strongly closed C in $I^+_{\kappa , \pi }$ . It is easy to see that $SNS_{\kappa , \pi }$ is a $\kappa $ -complete, fine ideal on $P_{\kappa } (\pi )$ . Furthermore, $SNS_{\kappa , \pi } \subset NS_{\kappa , \pi }$ .

Observation 4.1. $\{x \in P_{\kappa } (\pi ) : \psi (x) \geq \sup x\} \in SNS^{\ast }_{\kappa ,\pi }$ .

Proof It suffices to note that $\{x \in P_{\kappa } (\pi ) : \forall \xi \in x (ran (f_{\xi }) \subseteq x)\} \in SNS^{\ast }_{\kappa ,\pi }$ .

Let $\mu $ be a regular cardinal less than $\kappa $ . An ideal K on $P_{\kappa } (\pi )$ is $(\mu , \kappa )$ -normal if for any $G \in K^+$ and any $k : G \rightarrow P_{\mu } (\pi )$ with the property that $k (x) \subseteq x$ for every $x \in G$ , there is d in $P_{\kappa } (\pi )$ and $H \in K^+ \cap P (G)$ such that $f (x) \subseteq d$ for all $x \in H$ . We let denote the smallest fine, $\kappa $ -complete, $(\mu , \kappa )$ -normal ideal on . As observed in [33], the set of all $x \in P_{\kappa } (\pi )$ such that $\sup e \in x$ for all $e \in P_{\mu } (x)$ lies in $NS_{\mu , \kappa , \pi }^{\ast }$ . Furthermore, the set of all $x \in P_{\kappa } (\pi )$ such that $\sup x$ is a limit ordinal of cofinality $\mu $ lies in $NS_{\mu , \kappa , \pi }^+$ .

A subset C of $P_{\kappa } (\pi )$ is $\mu $ -closed if $\bigcup _{i < \mu } c_i \in C$ for every increasing sequence in $(C, \subset )$ . A subset D of $P_{\kappa } (\pi )$ is a $\mu $ -club if it is a $\mu $ -closed, cofinal subset of $P_{\kappa } (\pi )$ . We let $N\mu $ - $S_{\kappa ,\pi }$ be the set of all $H \subseteq P_{\kappa } (\pi )$ such that $H \cap D = \emptyset $ for some $\mu $ -club $D \subseteq P_{\kappa } (\pi )$ . Let $Y_{\mu }^{\kappa , \pi }$ denote the set of all nonempty $x \in P_{\kappa }(\pi )$ such that:

• • For any $\alpha \in x$ , $\alpha + 1 \in x$ .

• • For any regular infinite cardinal $\sigma \in \kappa \setminus \{\mu \}$ , and any increasing sequence of elements of x, $\sup \{\beta _{\xi } : \xi < \sigma \} \in x$ .

Notice that for any $x \in Y_{\mu }^{\kappa , \pi }$ and any cardinal of cofinality greater than or equal to $\kappa $ , $\sup (x \cap \tau )$ is a limit ordinal of cofinality $\mu $ . It is remarked in [30] that $Y^{\kappa , \pi }_{\mu }$ and the set $\{x \in P_{\kappa } (\pi ):\vert x\vert = \vert x \cap \kappa \vert \geq \mu \}$ are both $\mu $ -clubs.

Lemma 4.2.

1. (i) Suppose that $\vert A \vert < \mu $ . Then .

2. (ii) Suppose that I is $\mu ^+$ -complete. Then - $S_{\kappa ,\pi })^{\ast }$ .

Proof (i): Suppose toward a contradiction that the set $X = \{x \in P_{\kappa } (\pi ) : \psi (x)> \sup x\}$ lies in $NS_{\mu , \kappa , \pi }^+$ . For $x \in X$ , set $e_x = \{a \in A : \sup (x \cap a)> f_{\sup x} (a)\}$ , and select $s_x : e_x \rightarrow x$ so that $f_{\sup x} (a) < s_x (a) < a$ for all $a \in e_x$ . There must be $T \in NS_{\mu , \kappa , \pi }^+ \cap P (X)$ and such that $ran (s_x) \subseteq w$ for all $x \in T$ . Pick $x \in T$ such that . Then . On the other hand for any $a \in e_x$ , $\sup (w \cap a) \geq s_x (a)> f_{\sup x} (a)$ . This is a contradiction, since $e_x \in I^+$ .

(ii): We first establish the following.

Claim. Let be an increasing sequence in $(P_{\kappa } (\pi ), \subset )$ . Then .

Proof of the claim

For $i < \mu $ , put $v_i = \{a \in A : \sup (c_i \cap a)> f_{\psi (c_i)} (a)\}$ and $w_i = \{a \in A : f_{\psi (c_i)} (a)> f_{\sup \{\psi (c_r) : r < \mu \}} (a)\}$ . Then $\bigcup _{i < \mu } (v_i \cup w_i) \in I$ , and moreover for any $a \in A \setminus (\bigcup _{i < \mu } (v_i \cup w_i))$ , , which completes the proof of the claim.

By the claim, the set is $\mu $ -closed. To show that it is cofinal, fix $z \in P_{\kappa } (\pi )$ . Inductively define $c_i \in P_{\kappa } (\pi )$ for $i < \mu $ so that:

• • $c_0 = z$ .

• • $c_i \cup \{\psi (c_i)\} \subset c_{i + 1}$ for all $i < \mu $ .

Put $c = \bigcup _{i < \mu } c_i$ . Then clearly, $z \subseteq c$ . Moreover by the claim, , so $c \in C$ .

Observation 4.3.

1. (i) Suppose that $\vert A \vert < \mu $ . Then $ \{x \in P_{\kappa } (\pi ) : \psi (x) = \sup x\} \in NS_{\mu , \kappa , \pi }^{\ast }$ .

2. (ii) Suppose that I is $\mu ^+$ -complete. Then $ \{x \in P_{\kappa } (\pi ) : \psi (x) = \sup x\} \in (N\mu $ - $S_{\kappa ,\pi })^{\ast }$ .

Proof By Observation 4.1 and Lemma 4.2.

Observation 4.3 is of no use in the (critical) case when $\vert A \vert = \mu $ , which must be handled separately. In what follows we present Shelah’s approach, which is based on Namba combinatorics (that is, properties of trees of height $\omega $ ). So from here on to Observation 4.7 we suppose that ( $\mathrm {cf} (\theta ) = \omega $ and) $\vert A \vert = \aleph _0$ . Let be a one-to-one enumeration of A, and set ${\cal I} = u (I)$ , where $u : A \rightarrow \omega $ is defined by: $u (\theta _i) = i$ .

An ideal H on $\omega $ is a P-point if for any $F : \omega \rightarrow H$ , there is $G \in H^{\ast }$ such that $G \cap F (j)$ is finite for all $j < \omega $ .

Assume that ${\cal I}$ is a P-point (i.e., that given $B_n \in I$ for $n < \omega $ , there is $C \in I^{\ast }$ that meets each $B_n$ in a finite set). For $\alpha < \pi $ , define $F_{\alpha } \in \prod _{i < \omega } \theta _i$ by $F_{\alpha } (i) = f_{\alpha } (\theta _i)$ .

${\cal T}_{\pi }$ denotes the collection of all nonempty $T\subseteq \bigcup _{n < \omega } {}^n\pi $ such that for any $t \in T$ , $\{ t \vert n : n < \mathrm {dom} (t) \} \subseteq T$ and $\vert \{\alpha < \pi : t \cup \{(\mathrm {dom} (t), \alpha )\} \in T \} \vert = \pi $ .

Let $T \in {\mathcal T}_{\pi }$ . Set $[T] = \{ f\in {}^{\omega }\pi : \forall n < \omega (f \vert n \in T)\}$ . For $t \in T$ , put $T\ast t = \{ s \in T : s \subseteq t$ or $t \subseteq s\}$ . $[T]$ is endowed with the topology obtained by taking as basic open sets the members of the family $\{ [T \ast t] : t \in T \}$ .

Fact 4.4 [48, Lemma 2.14].

Suppose that $T \in {\cal T}_{\pi }$ , $\sigma < \pi $ is a cardinal, and $[T] = \bigcup _{\beta < \sigma } H_{\beta }$ , where each $H_{\beta }$ is Borel. Then there is $T' \in {\cal T}_{\pi } \cap P(T)$ and $\beta < \sigma $ such that $[T'] \subseteq H_{\beta }$ .

Let $\sigma $ be a cardinal greater than $\kappa $ , and let $\mu $ be a regular cardinal less than $\kappa $ . For $Q \subseteq P_{\kappa } (\sigma )$ , $G_{\kappa ,\sigma }^{\mu } (Q)$ denotes the following two-person game consisting of $\mu $ moves. At step $\alpha < \mu $ , player I selects $a_{\alpha } \in P_{\kappa } (\sigma )$ , and II replies by playing $b_{\alpha } \in P_{\kappa } (\sigma )$ . The players must follow the rule that for $\beta < \alpha < \mu $ , $b_{\beta }\subseteq a_{\alpha } \subseteq b_{\alpha }$ . II wins if and only if $\bigcup _{\alpha < \mu } a_{\alpha }\in Q$ .

$NG_{\kappa ,\sigma }^{\mu }$ denotes the collection of all $Q \subseteq P_{\kappa } (\sigma )$ such that II has a winning strategy in $G_{\kappa ,\sigma }^{\mu } (P_{\kappa } (\sigma ) \setminus Q)$ .

Fact 4.5 [25, 30, 35].

1. (i) $NG_{\kappa ,\sigma }^{\mu }$ is a $(\mu , \kappa )$ -normal ideal on $P_{\kappa } (\sigma )$ .

2. (ii) $N\mu $ - $S_{\kappa ,\sigma } \subseteq NG_{\kappa ,\sigma }^{\mu }$ .

3. (iii) Let $\tau> \sigma $ be a cardinal. Then $NG_{\kappa ,\sigma }^{\mu } = q (NG_{\kappa ,\tau }^{\mu })$ , where $q : P_{\kappa } (\tau ) \rightarrow P_{\kappa } (\sigma )$ is defined by $q (x) = x \cap \sigma $ .

4. (iv) If $\kappa = \omega _1$ (and $\mu = \omega $ ), then $NG_{\kappa ,\sigma }^{\mu } = NS_{\kappa ,\sigma }$ .

5. (v) There is a one-to-one function $y : \sigma ^{< \kappa } \rightarrow P_{\kappa } (\sigma )$ such that (a) for any $\beta \in \sigma $ , $\beta \in y (\beta )$ , and $(b) \ NG^{\omega }_{\kappa ,\sigma } = {\overline y} (NS_{\omega _1, \sigma ^{< \kappa }})$ , where ${\overline y} : P_{\omega _1} ( \sigma ^{< \kappa } )\rightarrow P_{\kappa } (\sigma )$ is defined by ${\overline y} (x) = \bigcup _{\delta \in x} y(\delta )$ .

The following generalizes a result of Shelah [54] (in which $\pi = \theta ^+$ and ${\cal I} = I_{\omega }$ ).

Lemma 4.6. Let $S \in NS_{\pi }^+ \cap P (E_{\omega }^{\pi })$ . Then

$$ \begin{align*} \{ b \in P_{\omega_1} (\pi) : \sup b \in S \text{ and } \psi (b) = \sup b )\} \in NS_{\omega_1, \pi}^+. \end{align*} $$

Proof Fix a closed unbounded subset C of $P_{\omega _1} (\pi )$ . Pick

so that:

• • For $h : \omega \rightarrow \pi $ , $k (h) = \bigcup _{n < \omega } k (h \vert n)$ .

• • For $t : m + 1 \rightarrow \pi $ , $\{ t (m) \} \cup k (t \vert m) \subseteq k (t)$ .

Clearly, if $h \in {}^{\omega }\pi $ , $i \in \omega $ , and $\beta \in \theta _i$ are such that $\varphi (k(h)) (\theta _i)> \beta $ , then $\varphi (k(h \vert m)) (\theta _i)> \beta $ for some m with . Hence, using Fact 4.4, we may construct inductively $T \in {\cal T}_{\pi }$ and $\chi : T \rightarrow \theta $ such that for any $t \in T$ and any $h \in [T\ast t]$ , .

We define a strategy $\tau $ for player II in $G_{\kappa ,\pi }^{\omega } (P_{\kappa } (\pi ))$ as follows. Consider a play of the game where I’s successive moves are $d_0, d_1, \dots $ . Using her strategy $\tau $ , II will successively play $e_0, e_1, \dots $ so that:

• • $d_j \cup \{ \psi (d_j) \} \subseteq e_j$ .

• • $\sup e_j$ is an infinite limit ordinal greater than $\sup d_j$ .

• • For any $t \in T$ with $\mathrm {ran} (t) \subseteq e_j$ , $\chi (t) \in e_j$ , and moreover

  $$ \begin{align*} \sup \{ \gamma \in e_j : t \cup \{ (\mathrm{dom} (t), \gamma)\} \in T \} = \sup e_j. \end{align*} $$

Now $\{ b \in P_{\omega _1} (\pi ) : \sup b \in S \} \in NS_{\omega _1, \pi }^+$ , so by Fact 4.5(iv), $\tau $ is not a winning strategy for II in $G_{\kappa ,\pi }^{\omega } (\{ b \in P_{\omega _1} (\pi ) : \sup b \notin S \})$ . Hence there must be a play of this game where I’s successive moves are $d_0, d_1, \dots $ , II successively plays $e_0, e_1, \dots $ using her strategy $\tau $ , and I wins. Thus $\sup e \in S$ , where $e = \bigcup _{j < \omega } e_j$ . Put $\delta = \sup e$ . Notice that for any $j < \omega $ , . It follows that , since $\psi (d_{j + 1}) \in e_{j + 1}$ . Define $\unicode{x0142} :\omega \rightarrow {\cal I }$ by $\unicode{x0142} (j) = \{ i < \omega : \varphi (e_j) (\theta _i)> F_{\delta } (i) \}$ . By P-pointness of ${\cal I}$ , there must be $G \in {\cal I}^{\ast }$ such that $G \cap \unicode{x0142} (j)$ is finite for all $j < \omega $ . Pick an increasing sequence $< n_j : j < \omega>$ of elements of $\omega $ so that whenever $j < \omega $ and $i \in G \setminus n_j$ . Now construct $h \in [T]$ so that $\{h (i) : i < n_0\} \subseteq e_0$ , and for any $j < \omega $ :

• • $h(i) \in e_j$ whenever ;

• • $h(n_{j + 1})> \sup (e_j)$ .

Put $b = k (h)$ . Then clearly, $b \in C$ , and moreover $\mathrm {ran} (h) \subseteq b$ . It follows that .

Claim. Let $j < \omega $ and $i \in G$ with . Then .

Proof of the claim

Since $\mathrm {ran} (h \vert i) \subseteq e_j$ , $\chi (h \vert i) \in e_j \cap \theta _i$ . Hence, , which completes the proof of the claim.

It follows from the claim that . Thus, , so $\sup b = \psi (b)$ .

Observation 4.7. Let $S \in NS_{\pi }^+ \cap P (E_{\omega }^{\pi })$ . Then

$$ \begin{align*} \{ w \in P_{\kappa} (\pi) : \sup w \in S \text{ and } \psi (w)= \sup w\} \in (NG^{\omega}_{\kappa,\pi})^+. \end{align*} $$

Proof For $\kappa = \omega _1$ , this is just Lemma 4.6. Let us now assume that $\kappa> \omega _1$ . Set

$$ \begin{align*} Q = \{ x \in P_{\omega_1} (\pi^{< \kappa}) : \sup (x \cap \pi) \in S \text{ and } \psi (x \cap \pi) = \sup (x \cap \pi )\}. \end{align*} $$

Then by Fact 4.5(iii) and (iv) and Lemma 4.6, $Q \in NS_{\omega _1,\pi ^{< \kappa }}^+$ . By Fact 4.5(v), we may find $y : \pi ^{< \kappa } \rightarrow P_{\kappa } (\pi )$ such that (a) for any $\beta \in \pi $ , $\beta \in y (\beta )$ , and (b) $NG^{\omega }_{\kappa ,\pi } = {\overline y} (NS_{\omega _1, \pi ^{< \kappa }})$ , where ${\overline y} : P_{\omega _1} ( \pi ^{< \kappa } )\rightarrow P_{\kappa } (\pi )$ is defined by ${\overline y} (x) = \bigcup _{\delta \in x} y(\delta )$ . Note that $x \cap \pi \subseteq {\overline y} (x)$ for all $x \in P_{\omega _1} (\pi ^{< \kappa })$ . Put $c = \{ i < \omega : \theta _i \geq \kappa \}$ . Note that $c \in {\cal I}^{\ast }$ . Let C denote the set of all infinite $x \in P_{\omega _1} (\pi ^{< \kappa })$ such that:

• • For any $\eta \in x$ and any $i \in c$ , there is $\beta \in x \cap \theta _i$ with $\sup (y (\eta ) \cap \theta _i) < \beta $ .

• • For any $\eta \in x$ , there is $\beta \in x \cap \pi $ with $\sup (y (\eta )) < \beta $ .

Then clearly, C is a closed unbounded subset of $P_{\omega _1} (\pi ^{< \kappa })$ . Furthermore for any $x \in C$ , $\psi (x \cap \pi ) = \psi ({\overline y} (x))$ and $\sup (x \cap \pi ) = \sup ({\overline y} (x))$ . Thus ${\overline y}" (Q \cap C)$ lies in $(NG^{\omega }_{\kappa ,\pi })^+$ , and moreover it is included in the set $\{ w \in P_{\kappa } (\pi ) : \sup w \in S$ and $\psi (w)= \sup w\}$ .

For any $S \in (NS_{\pi } \vert E_{\omega }^{\pi })^+$ , $\{ w \in P_{\kappa } (\pi ) : \psi (w) \in S\} \in (NG^{\omega }_{\kappa ,\pi })^+$ by Observation 4.7, and therefore by Fact 4.5(iii). Thus . Let us observe that it is not necessarily the case that $\psi " W \in NS_{\pi }^+$ for all . To see this, recall that the bounding number $\mathfrak {b}_{\pi }$ denotes the least cardinality of any $F \subseteq {}^{\pi } \pi $ with the property that there is no $g \in {}^{\pi } \pi $ such that $\vert \{\beta < \pi : f (\beta ) \geq g (\beta \} \vert < \pi $ for all $f \in F$ .

Fact 4.8 [2].

$\mathfrak {b}_{\pi }$ is the least cardinality of any collection F of closed unbounded subsets of $\pi $ such that for any $B \in [\pi ]^{\pi }$ , there is $C \in F$ with $\vert B \setminus C \vert = \pi $ .

Observation 4.9. Let K be an ideal on such that and $\overline {\mathrm {cof}} (K) < \mathfrak {b}_{\pi }$ . Then there is $D \in NS_{\pi }^{\ast }$ such that .

Proof Put $\sigma = \overline {\mathrm {cof}} (K)$ . We have that . Now , so we may find $C_{\alpha } \in NS_{\pi }^{\ast }$ for $\alpha < \sigma $ such that for any , there is $z \in P_{\kappa } (\sigma ) \setminus \{\emptyset \}$ with the property that $(\bigcap _{\alpha \in z} C_{\alpha }\big ) \cap E_{\omega }^{\pi } \subseteq X$ . Using Fact 4.8, select $D \in NS_{\pi }^{\ast }$ so that $\vert D \setminus C_{\alpha } \vert < \pi $ for every $\alpha < \sigma $ . Now fix $T \in I_{\pi }^+ \cap P(D\cap E_{\omega }^{\pi })$ . Clearly $T \setminus \bigcup _{\alpha \in z} (D \setminus C_{\alpha }) \subseteq \bigcap _{\alpha \in z} C_{\alpha }$ for every $z \in P_{\kappa } (\sigma ) \setminus \{\emptyset \}$ , so $T \cap X \not = \emptyset $ for all . Hence .

Set and . Then , so by Observation 4.9, there must be $D \in NS_{\pi }^{\ast }$ such that . Select T in $I_{\pi }^+ \cap NS_{\pi } \cap P (D \cap E^{\pi }_{\omega })$ , and put . Then clearly, , and moreover $\psi " W \in NS_{\pi }$ .

Another comment is in order. In contrast to Observation 4.3, the conclusion of Observation 4.7 does not assert that the set $\{ w \in P_{\kappa } (\pi ) : \sup w \in S$ and $\psi (w)= \sup w\}$ lies in the dual filter ( $(NG^{\omega }_{\kappa ,\pi })^{\ast }$ ), but only that it does not lie in the ideal ( $(NG^{\omega }_{\kappa ,\pi })$ ). There is a good reason for this. In fact if $\mu = \vert A \vert = \mathrm {cf} (\theta )$ , $\theta ^{< \mu } < \pi $ , and $Z \in NS_{\pi }^+ \cap P(E_{\mu }^{\pi })$ lies in the approachable ideal $I [\pi ]$ , then by a result of [30], for any $\ell : \pi \rightarrow \pi $ ,

$$ \begin{align*} \{ x \in P_{\kappa} (\pi) : \sup x \in Z \text{ and } \psi (x)> \ell (\sup x )\} \in (NG^{\mu}_{\kappa,\pi})^+. \end{align*} $$

On the other hand, we have the following.

Observation 4.10. Let $X \subseteq P_{\kappa } (\pi )$ be such that $\vert \{x \in X : \sup x = \beta \} \vert < \pi $ for all $\beta < \pi $ . Then there is $\ell : \pi \rightarrow \pi $ with the property that for all $x \in X$ .

Proof For $\beta < \pi $ , put $e_{\beta } = \{x \in X : \sup x = \beta \}$ . Now define $\ell : \pi \rightarrow \pi $ by: $\ell (\beta )$ equals $\sup \{\psi (x) : x \in e_{\beta }\}$ if $e_{\beta } \not = \emptyset $ , and $0$ otherwise.

Note that if $V = L$ , then by a result of Dieter Donder, for any stationary $Y \subseteq P_{\kappa } (\pi )$ , there exists a stationary $X \subseteq Y$ such that for all $\beta < \pi $ .

Let us finally observe that if $x = ran (f_{\alpha })$ , where $\alpha < \pi $ , then obviously $\psi (x) = \alpha $ . This shows that $\psi (x)$ needs not be a limit ordinal. On the other hand, by Observation 4.7 (respectively, Observation 4.3), if $\vert A \vert = \mu = \omega $ (respectively, $\vert A \vert < \mu $ or I is $\mu ^+$ -complete), the set of all x such that $\psi (x)$ is a limit ordinal of cofinality $\mathrm {cf} (\vert x \cap \theta \vert ) (= \mu )$ lies in $(NG_{\kappa ,\pi }^{\mu })^+$ (respectively, $(NG_{\kappa ,\pi }^{\mu })^{\ast }$ ). One intriguing question which is left unanswered by the results of the next section is whether the set of all x such that $\psi (x)$ is a limit ordinal of cofinality $(\mathrm {cf} (\vert x \cap \theta \vert ))^+$ lies in $J^{\ast }$ for any weakly $\pi $ -saturated, normal, fine ideal J on .

5 The way of Usuba

As in the preceding section, we assume in this one that , and we look for strategies to deal with situations when our ideal J on cannot be shown to be isomorphic to a nice ideal on $P_{\kappa } (\pi )$ . Sticking with ideals, we could attempt to bypass $P_{\kappa } (\pi )$ and associate J with an ideal on $\pi $ of the form $h (J)$ for some . But there are obvious difficulties. One is that $h (J)$ will be $\kappa $ -complete (when we would be more comfortable with $\pi $ -completeness). Another is that if , then J and $h (J)$ will not be isomorphic. So instead we will follow Usuba [60] whose method consists in moving from J (to its projection on $P_{\kappa } (\theta )$ and then) to an ideal K on $P_{\kappa } (\theta )$ with which is associated a function h taking its values in $\pi $ . The crux of the matter is that if J is weakly $\pi $ -saturated, then so is K.

An ideal on $P_{\kappa } (\sigma )$ , where $\sigma $ is a cardinal greater than or equal to $\theta $ , is adequate if it is $\kappa $ -complete in case $\kappa $ is a successor cardinal, and $\theta $ -normal otherwise.

Let J be an adequate, fine ideal on . We put ${\cal J} = p (J)$ , where is defined by $p (c) = c \cap \theta $ .

Observation 5.1.

1. (i) ${\cal J}$ is an adequate, fine ideal on $P_{\kappa } (\theta )$ .

2. (ii) If J is $\theta $ -normal, then ${\cal J}$ is normal.

3. (iii) If J is weakly $\pi $ -saturated, then so is ${\cal J}$ .

Fact 5.2 [60].

1. (i) There exist a function $h : P_{\kappa } (\theta ) \rightarrow On$ and an adequate ideal K on $P_{\kappa } (\theta )$ extending ${\cal J}$ such that:

   • • For any $X \in K^+$ and any $g \in \prod _{b \in X} h (b)$ , there is $\beta < \pi $ with .

   • • For each $\gamma < \pi $ , $\{ b \in P_{\kappa } (\theta ) : h (b)> \gamma \} \in K^{\ast }$ .

2. (ii) K is weakly $\pi $ -saturated if and only if for any $X \in K^{\ast }$ and any $g \in \prod _{b \in X} h (b)$ , there is $\beta < \pi $ with .

3. (iii) If ${\cal J}$ is weakly $\pi $ -saturated, then so is K.

4. (iv) If ( $\kappa $ is a successor and) ${\cal J}$ is normal, then so is K.

We should stress that $\psi $ (or, for that matter, the fact that $\theta $ is singular) does not play any role in the definition of h and K.

Observation 5.3.

1. (i) .

2. (ii) Let C be a closed unbounded subset of $\pi $ . Then $h^{- 1} (C) \in K^{\ast }$ .

3. (iii) Let $C_{\vec {f}}$ be as in the statement of Fact 3.8(i). Then $\{b \in P_{\kappa } (\theta ) : h (b) \in C_{\vec {f}}\} \in K^{\ast }$ .

4. (iv) Suppose that K is weakly $\pi $ -saturated, and let W be a stationary subset of $\pi $ such that $\mathrm {cf} (\gamma ) < \kappa $ for all $\gamma \in W$ . Then the set of all $b \in P_{\kappa } (\theta )$ such that $W \cap h (b)$ is stationary in $h (b)$ lies in $K^{\ast }$ .

Proof For (i) (respectively, (ii) and (iv)), the proof is a straightforward modification of that of Proposition 4.1 (respectively, 4.2 and 4.3) of [60]. As for (iii), it is immediate from (ii).

Concerning (iv), notice that by $\kappa $ -completeness of K, we can actually simultaneously reflect less than $\kappa $ many stationary sets. By Theorem 2.13 in [15], it follows that if J (and hence K) is weakly $\pi $ -saturated, then the square principle $\square (\pi , < \sigma )$ fails for every regular cardinal $\sigma < \kappa $ .

Observation 5.4. Suppose that K is weakly $\pi $ -saturated. Then the set of all $b \in P_{\kappa } (\theta )$ such that $\mathrm {cf} (h (b))> o.t. (b)$ lies in $K^{\ast }$ .

Proof Suppose otherwise. Then the set Q of all $b \in P_{\kappa } (\theta )$ with lies in $K^+$ . Define $r : P_{\kappa } (\theta ) \rightarrow P_{\kappa } (\theta )$ by: $r (b)$ equals b if $\kappa $ is weakly inaccessible, and $\nu $ if $\kappa = \nu ^+$ . For $b \in Q$ , pick $t_b : r (b) \rightarrow h (b)$ such that $\sup (ran (t_b)) = h (b)$ . Let $\chi = \theta $ if $\kappa $ is weakly inaccessible, and $\chi = \nu $ if $\kappa = \nu ^+$ . We define $s : \chi \rightarrow \pi $ , and $Q_{\gamma } \in (K \vert Q)^{\ast } \cap P (Q)$ for $\gamma < \chi $ , as follows. Put $W = \{b \in P_{\kappa } (\theta ) : h (b)> 0\}$ . Notice that $W \in K^{\ast }$ . Given $\gamma < \chi $ , set $W_{\gamma } = W \cap \{b \in P_{\kappa } (\theta ) : \gamma \in b\}$ , and define $g_{\gamma } \in \prod _{b \in W_{\gamma }} h (b)$ by: $g_{\gamma } (b)$ equals $t_b (\gamma )$ if $b \in Q$ , and $0$ otherwise. Since K is weakly $\pi $ -saturated, we may find $\xi _{\gamma } < \pi $ such that $X_{\gamma } \in K^{\ast }$ , where . We now let $s (\gamma ) = \xi _{\gamma }$ . Notice that for all $b \in Q \cap X_{\gamma }$ .

Since K is adequate, the set of all $b \in P_{\kappa } (\theta )$ such that $b \in X_{\gamma }$ for all $\gamma \in b \cap \chi $ lies in $K^{\ast }$ . Hence we may select $b \in Q$ such that (a) $h (b)> \sup (ran (s))$ , and (b) $b \in X_{\gamma }$ for all $\gamma \in r (b)$ . Then

Contradiction.

Observation 5.5.

1. (i) Let $z_{\alpha } \in P_{\kappa } (\theta )$ for $\alpha < \pi $ . Then

   $$ \begin{align*} \{ b \in P_{\kappa} (\theta) : \sup \{ \alpha < h (b) : z_{\alpha} \subseteq b \}= h (b) \} \in K^{\ast}. \end{align*} $$

2. (ii) Suppose that there is $z_{\alpha } \in P_{\kappa } (\theta )$ for $\alpha < \pi $ so that the set of all $b \in P_{\kappa } (\theta )$ such that lies in $K^{\ast }$ .Then the set of all $b \in P_{\kappa } (\theta )$ such that $\vert b \vert \geq \mathrm {cf} (h (b))$ lies in $K^{\ast }$ .

Observation 5.6. Suppose that K is weakly $\pi $ -saturated. Then the set of all $b \in P_{\kappa } (\theta )$ such that $h (b)$ is not a good point for ${\vec f}$ lies in $K^{\ast }$ .

Proof Recall from Section 3 that for $\alpha < \pi $ , $y_{\alpha }$ equals $\{\alpha \}$ if $\alpha < \theta $ , and $\{\Phi (a, f_{\alpha } (a)) : a \in A \}$ otherwise. Assume toward a contradiction that the desired conclusion fails. Then by Observations 5.4 and 5.5(i), we may find $b \in P_{\kappa } (\theta )$ such that $\mathrm {cf} (h (b))> o.t. (b)$ , $h (b)$ is a good point for ${\vec f}$ , and $\sup z = h (b)$ , where $z = \{ \alpha < h (b) : y_{\alpha } \subseteq b \}$ . Then, by Observation 3.7, $\vert \bigcup _{\alpha \in z} y_{\alpha } \vert \geq \mathrm {cf} (h (b))> \vert b \vert $ . Contradiction.

Observation 5.7. Suppose that K is weakly $\pi $ -saturated. Then the set of all $b \in P_{\kappa } (\theta )$ such that lies in $K^{\ast }$ .

Proof Assume that the conclusion fails. By [28, Lemmas 4.2 and 4.7], there is an increasing, cofinal sequence in $(\prod A, <_I)$ with the property that for any cardinal $\sigma $ with $\vert A \vert < \sigma < \theta $ , and any order-type $\sigma ^{+ 3}$ subset v of $\pi $ , there is an order-type $\sigma $ subset w of v such that the sequence is strongly increasing. For $\alpha < \pi $ , put $z_{\alpha } =\{\Phi (a, k_{\alpha } (a)) : a \in A \}$ . By Observation 5.5(i), there must be $b \in P_{\kappa } (\theta )$ such that:

• • $\vert b \vert \geq \vert A \vert $ .

• • $\mathrm {cf} (h (b))> \vert b \vert ^{+ 3}$ .

• • $\sup \{ \alpha < h (b) : z_{\alpha } \subseteq b \}= h (b)$ .

Now select an order-type $(\vert b \vert ^+)^{+ 3}$ subset v of $\{ \alpha < h (b) : z_{\alpha } \subseteq b \}$ . We may find an order-type $\vert b \vert ^+$ subset w of v, and $Z_{\xi } \in I$ for $\xi \in w$ such that $k_{\xi _1} (a) < k_{\xi _2} (a)$ whenever $a \in A \setminus (Z_{\xi _1} \cup Z_{\xi _2})$ . Pick $t \in \prod _{\xi \in w} (A \setminus Z_{\xi })$ , and set $c = \{\Phi (t (\xi ), k_{\xi } (t (\xi ))) : \xi \in w \}$ . Then clearly, $c \subseteq b$ . However $\vert c \vert = \vert b \vert ^+$ , which is a contradiction.

The ideal ${\cal K} = h (K)$ does have some interesting properties, but it is not clear what can be gained by considering it. By Fact 5.2 and Observations 5.3 and 5.6, the following hold:

• • ${\cal K}$ is a $\kappa $ -complete ideal on $\pi $ extending $NS_{\pi }$ .

• • If K is weakly $\pi $ -saturated, then so is ${\cal K}$ .

• • For any $X \in {\cal K}^+$ and any $g : X \rightarrow \pi $ such that $g (\gamma ) < \gamma $ for all $\gamma \in X$ , there is $\beta < \pi $ with .

• • Suppose that K is weakly $\pi $ -saturated. Then (a) for any $X \in {\cal K}^{\ast }$ and any $g : X \rightarrow \pi $ such that $g (\gamma ) < \gamma $ for all $\gamma \in X$ , there is $\beta < \pi $ with , and (b) the set of all $\gamma \in \pi $ such that $\gamma $ is not a good point for ${\vec f}$ lies in ${\cal K}^{\ast }$ .

A function $g \in \prod A$ is an exact upper bound for some $F \subseteq \{ f_{\alpha } : \alpha < \pi \}$ if (a) for all $f \in F$ , and (b) for any $k \in \prod A$ with $k <_I g$ , there is $f \in F$ with $k <_I f$ .

Fact 5.8 ([50, Claim 1.6, p. 52] (see also [1, Exercise 2.6])).

Let e be a subset of $\pi $ such that $\sup e \notin e$ and $\mathrm {cf} (\sup e)> \vert A \vert $ . Then the following are equivalent:

1. (i) $\sup e$ is a good point for ${\vec f}$ .

2. (ii) The sequence has an exact upper bound g such that the set of all $a \in A$ such that $g (a)$ is a limit ordinal of cofinality $\mathrm {cf} (\sup e)$ lies in $I^{\ast }$ .

An infinite limit ordinal $\delta < \pi $ is a more-than-good point for $\vec f$ if there is a cofinal subset X of $\delta $ , and $Z_{\xi } \in I$ for $\xi \in X$ such that $f_{\beta } (a) < f_{\xi } (a)$ whenever $\beta < \xi $ are in X and $a \in A \setminus Z_{\xi }$ . By results of Shelah, for any regular cardinal $\mu $ with $\vert A \vert < \mu < \theta $ , the set of all good points for ${\vec f}$ of cofinality $\mu $ is stationary in $\pi $ . This is also true of more-than-good points.

Observation 5.9. Let $\mu $ be a regular cardinal with $\vert A \vert < \mu < \kappa $ . Then the set of all $x \in P_{\kappa } (\pi )$ such that $\sup x$ is a more-than-good point for ${\vec f}$ lies in $(NS_{\mu , \kappa , \pi } \vert \{x : \mathrm {cf} (\sup x) = \mu \})^{\ast }$ .

Proof For $e \in P_{\mu } (\pi )$ , define $g_e \in \prod A$ by: $g_e (a)$ equals $\sup \{f_{\beta } (a) : \beta \in e \}$ if $a \geq \mu $ , and 0 otherwise. Let X be the set of all $x \in P_{\kappa } (\pi )$ such that for any $e \in P_{\mu } (x)$ , there is $\alpha \in x$ with $g_e <_I f_{\alpha }$ .

Claim. $X \in NS_{\mu , \kappa , \pi }^{\ast }$ .

Proof of the claim

Suppose otherwise. For $x \in P_{\kappa } (\pi ) \setminus X$ , select $e_x \in P_{\mu } (x)$ such that there is no $\alpha \in x$ with $g_{e_x} <_I f_{\alpha }$ . We may find $W \in NS_{\mu , \kappa , \pi }^+$ and $b \in P_{\kappa } (\pi )$ such that $e_x \subseteq b$ for all $x \in W$ . Define $\unicode{x0142} \in \prod A$ by: $\unicode{x0142} (a)$ equals $\sup \{f_{\gamma } (a) : \gamma \in b \}$ if $a \geq \kappa $ , and 0 otherwise. Pick $\alpha < \pi $ with $\unicode{x0142} <_I f_{\alpha }$ . Now there must be $x \in W$ with $\alpha \in x$ . This contradiction completes the proof of the claim.

Given $x \in X$ with $\mathrm {cf} (\sup x) = \mu $ , pick an increasing sequence of ordinals with supremum $\sup x$ . Inductively define $\alpha _i \in x \setminus \xi _i$ and $Z_i \in I$ for $i < \mu $ so that for any $i < \mu $ and any $a \in A \setminus Z_i$ , $g_{\{\alpha _j : j < i\}} (a) < f_{\alpha _i} (a)$ . Then clearly, $f_{\alpha _j} (a) < f_{\alpha _i} (a)$ whenever $j < i < \mu $ and $a \in A \setminus Z_i$ .

Corollary 5.10. Let $\mu $ be a regular cardinal with $\vert A \vert < \mu < \theta $ . Then there are stationarily many more-than-good points for ${\vec f}$ of cofinality $\mu $ .

For $b \in P_{\kappa } (\theta )$ , let $d_b$ be the set of all $\delta \in b$ such that $o.t. (b \cap \delta )$ is a regular cardinal greater than $\vert A \vert $ . For $\delta \in d_b$ , let $G^b_{\delta }$ be the set of all $\beta < h (b)$ with $\mathrm {cf} (\beta ) = o.t. (b \cap \delta )$ with the property that $\beta $ is a good point for . Let $\Omega $ be the set of all $b \in P_{\kappa } (\theta )$ such that $G^b_{\delta }$ is stationary in $h (b)$ for all $\delta \in d_b$ .

Lemma 5.11. Suppose that K is weakly $\pi $ -saturated. Then $\Omega \in K^{\ast }$ .

Proof The proof is a modification of that of Claim 5.2 in [60]. Suppose that the conclusion fails. Then we may find $X \in K^+$ , $\tau < \theta $ , and $c_b$ for $b \in X$ such that for each $b \in X$ , (a) $\tau \in d_b$ , (b) $c_b$ is a closed unbounded subset of $h (b)$ of order type $\mathrm {cf} (h (b))$ , and (c) $G^b_{\tau } \cap c_b = \emptyset $ .

Claim. $\tau $ is a regular cardinal.

Proof of the claim

It suffices to observe the following:

Case when $\kappa $ is a successor cardinal, say $\kappa = \nu ^+$ . Pick $x \in X$ with $\nu + 1 \subseteq x$ . We must have , since otherwise $\nu < o.t. (x \cap \tau ) = \vert x \cap \tau \vert = \nu $ . But then $x \cap \tau = \tau = o.t. (x \cap \tau )$ .

Case when $\kappa $ is weakly inaccessible. Given $q \subseteq \tau $ and an increasing function $k : q \rightarrow \tau $ with the property that $\sup (ran (k)) = \sup \tau $ , the set of all $b \in P_{\kappa } (\theta )$ with $\sup (k" (b \cap q)) = \sup (b \cap \tau )$ lies in $NS^{\ast }_{\kappa , \theta }$ .

It is simple to see that $\tau> \vert A \vert $ . Inductively construct $u_{\xi } \in P_{\tau } (\pi )$ , $\delta _{\xi } < \pi $ and $T_{\xi } \in (K \vert X)^{\ast }$ for $\xi < \tau $ such that:

• • $u_{\xi } \subseteq u_{\xi + 1}$ .

• • $u_{\xi } = \bigcup _{\zeta < \xi } u_{\zeta }$ in case $\xi $ is an infinite limit ordinal.

• • $\varphi (u_{\xi }) <_I f_{\delta _{\xi }}$ .

• • $ran (f_{\delta _{\xi }}) \subseteq u_{\xi + 1}$ .

• • For any $b \in X \cap T_{\xi }$ , $h (b)> \sup u_{\xi }$ , and moreover the least $\eta \in c_b$ with $\eta \geq \sup u_{\xi }$ is less than $\sup u_{\xi + 1}$ .

We may find $b \in X$ such that (1) $\mathrm {cf} (h (b))> o.t. (b)$ , and (2) $b \in T_{\xi }$ for all $\xi \in b \cap \tau $ . Set $\beta = \sup (\bigcup _{\xi < \sup (b \cap \tau )} u_{\xi })$ . Clearly, $\mathrm {cf} (\beta ) = o.t. (b \cap \tau )$ . Moreover, since $o.t. (c_b) = \mathrm {cf} (h (b))> o.t. (b) \geq o.t. (b \cap \tau )$ , we have that $\beta \in c_b$ . Pick $e \subseteq \sup (b \cap \tau )$ so that $o.t. (e) = \mathrm {cf} (\beta )$ and $\sup e = \sup (b \cap \tau )$ . For $\xi \in e$ , , so there is $Z_{\xi } \in I$ such that $A \cap \kappa \subseteq Z_{\xi }$ , and moreover for all $a \in A \setminus Z_{\xi }$ . Now let $\zeta < \xi $ in e. Then for any $a \in A \setminus (Z_{\delta } \cup Z_{\xi })$ , . Thus $\beta $ is a good point for . Contradiction.

For $b \in P_{\kappa } (\theta )$ , let $w_b$ be the set of all those $\delta < h (b)$ of cofinality $\vert b \vert ^+$ that are good points for . Assuming that K is weakly $\pi $ -saturated, it is easy to show that, in contrast to Lemma 5.11, the set of all $b \in P_{\kappa } (\theta )$ such that $w_b$ is stationary in $h (b)$ lies in K. Suppose otherwise. By Observations 5.4 and 5.5(i), there must be $b \in P_{\kappa } (\theta )$ such that (a) $w_b$ is stationary in $h (b)$ , (b) $\sup \{\alpha < h (b) : y_{\alpha } \subseteq b\} = h (b)$ (where is the sequence defined in Section 3), and (c) $\mathrm {cf} (h (b))> \vert b \vert \geq \vert A \vert $ . Pick $z \subseteq \{ \alpha < h (b) : y_{\alpha } \subseteq b \}$ with $o.t. (z) = \mathrm {cf} (h (b))$ and $\sup z = h (b)$ . We may find $\delta \in w_b$ such that $\sup (z \cap \delta ) = \delta $ . But then by Observation 3.7, $\vert \bigcup \{y_{\alpha } : \alpha \in z \cap \delta \} \vert \geq \mathrm {cf} (\delta )> \vert b \vert $ , which yields the desired contradiction.

Let $\Xi $ be the set of all $b \in P_{\kappa } (\theta )$ with the property that has an exact upper bound g such that for each regular cardinal $\sigma $ with .

Lemma 5.12. Suppose that $\vert A \vert ^+ < \kappa $ and K is weakly $\pi $ -saturated. Then $\Xi \in K^{\ast }$ .

Proof Let B be the set of all $b \in \Omega $ such that $\sup b = \theta $ and $\vert A \vert < \vert b \vert < \mathrm {cf} (h (b))$ . By Observation 5.4 and Lemma 5.11, $B \in K^{\ast }$ . We will show that $B \subseteq \Xi $ . Thus let $b \in B$ .

Claim. Let $\sigma $ be a regular cardinal with . Then there are stationarily many good points for of cofinality $\sigma $ .

Proof of the claim

We have that , so $\sigma < o.t. (b)$ . Hence there must be $\delta \in b$ such that $o.t. (b \cap \delta ) = \sigma $ . Since $b \in \Omega $ , the claim follows.

By Lemmas 15 and 16 of [22], it follows from the claim that $b \in \Xi $ .

Lemma 5.13. $\Theta \in K^{\ast }$ , where $\Theta $ denotes the set of all $b \in P_{\kappa } (\theta )$ such that if g is an exact upper bound for , then

$$ \begin{align*} \{ a \in A : \sup (g (a) \cap b) = g (a)\} \in I^{\ast}. \end{align*} $$

Proof The proof is a straightforward modification of that of Lemma 4.5 in [60].

Observation 5.14. Suppose that $\vert A \vert ^+ < \kappa $ and K is weakly $\pi $ -saturated. Then ${\mathfrak A} \in K^{\ast }$ , where ${\mathfrak A}$ denotes the set of all $b \in P_{\kappa } (\theta )$ such that $(a) \ \vert b \vert $ is a singular cardinal of cofinality at most $\vert A \vert $ , $(b) \ I$ is not $(\mathrm {cf} (\vert b \vert ))^+$ -complete, and $(c) \ \mathrm {pp} (\vert b \vert ) \geq \mathrm {cf} (h (b))$ .

Proof Let B be the set of all $b \in \Xi \cap \Theta $ such that:

• • .

• • $h (b) \in C_{\vec f}$ .

• • $h (b)$ is not a good point for ${\vec f}$ .

Then by Observations 5.3(iii), 5.4, 5.6, and 5.7 and Lemmas 5.12 and 5.13, $B \in K^{\ast }$ . Let us show that $B \subseteq {\mathfrak A}$ . Thus fix $b \in B$ . Since $b \in \Xi $ , has an exact upper bound g such that for each regular cardinal $\sigma $ with . On the other hand, $b \in \Theta $ , so the set of all a such that lies in $I^{\ast }$ . It follows that $\vert b \vert $ is not regular. As , $\vert b \vert $ must be the largest limit cardinal less than or equal to $\mathrm {cf} (h (b))$ . Now $h (b)$ lies in $C_{\vec f}$ , and moreover it is not a good point for ${\vec f}$ . Hence , I is not $(\mathrm {cf} (\vert b \vert ))^+$ -complete, and (c) .

Theorem 5.15.

1. (i) Suppose that $\kappa $ is weakly inaccessible and J is weakly $\pi $ -saturated. Then ${\mathcal X} \in J^{\ast }$ , where ${\mathcal X}$ denotes the set of all such that $(a) \ \vert x \cap \theta \vert $ is a singular cardinal of cofinality less than or equal to $\vert A \vert $ and $(b) \ I$ is not $(\mathrm {cf} (\vert x \cap \theta \vert ))^+$ -complete.

2. (ii) Suppose that $\kappa $ is a successor cardinal, say $\kappa = \nu ^+$ , and J is weakly $\pi $ -saturated. Then either $\nu = \vert A \vert $ , or and I is not $(\mathrm {cf} (\nu ))^+$ -complete.

Proof

1. (i): By Fact 1.6(iii) and (the proof of) Observation 5.14, ${\mathcal X} \in (J\vert X)^+$ for every $X \in J^+$ . It follows that ${\mathcal X} \in J^{\ast }$ .

2. (ii): By Observation 5.14.

Corollary 5.16.

1. (i) Suppose that $\kappa $ is weakly inaccessible, J is weakly $\pi $ -saturated, and ( $\vert A \vert = \mathrm {cf} (\theta )$ and) I is $\vert A \vert $ -complete. Then the set of all such that $\mathrm {cf} (\vert x \cap \theta \vert ) = \mathrm {cf} (\theta )$ lies in $J^{\ast }$ .

2. (ii) Suppose that $\kappa $ is a successor cardinal, say $\kappa = \nu ^+$ , J is weakly $\pi $ -saturated, and ( $\vert A \vert = \mathrm {cf} (\theta )$ and) I is $\vert A \vert $ -complete. Then $\mathrm {cf} (\nu ) = \mathrm {cf} (\theta )$ .

Here is one result that specifically addresses the situation when $\mathrm {pp} (\theta ) > \theta ^+$ .

Observation 5.17. Suppose that $\kappa $ is weakly inaccessible, J is normal, and $M \in J^+$ , where M denotes the set of all such that $\vert x \vert \geq \vert x \cap \theta \vert ^{+ 3}$ . Then J is not weakly $\pi $ -saturated.

Claim. There is a cardinal $\sigma $ such that the set $N_{\sigma }$ of all $x \in M$ with $\vert x \cap \sigma \vert = \vert x \cap \theta \vert ^{+ 3}$ lies in $J^+$ .

Proof of the claim

Suppose that . Then by normality of J, we may find $X \in J^+ \cap P (M)$ and such that for any $x \in X$ , $\gamma \in x$ , and moreover $o.t. (x \cap \gamma ) = \vert x \cap \theta \vert ^{+ 3}$ . Put $\tau _1 = \vert \gamma \vert $ and $\tau _2 = \tau _1^+$ . Since , there must be $j \in \{1, 2\}$ and $D \in J^+ \cap P (X)$ such that $\vert x \cap \gamma \vert = \vert x \cap \tau _j \vert $ for all $x \in D$ . Set $\sigma = \tau _j$ . Then clearly, $D \subseteq N_{\sigma }$ , which completes the proof of the claim.

By Theorem 5.15(i), the set Q of all such that $\vert x \cap \theta \vert $ is a singular cardinal greater than $\vert A \vert $ lies in $J^{\ast }$ . By Corollary 3.15, we may find $x \in Q \cap N_{\sigma }$ and $\delta \in C_{\vec {f}}$ such that (a) $\delta $ is not a good point for $\vec {f}$ , and (b) $\mathrm {cf} (\delta ) = \vert x \cap \sigma \vert ^+ = \vert x \cap \theta \vert ^{+ 4}$ . But clearly, $\vert x \cap \theta \vert $ is the largest limit cardinal less than or equal to $\mathrm {cf} (\delta )$ . By Fact 3.8(i), this yields the desired contradiction.

In situations when the scale is not good and $\mathrm {cf} (\vert x \cap \theta \vert ) = \vert A \vert $ , the following approach will help.

Pick a sequence of pairwise disjoint stationary subsets of $\{ \alpha < \pi : \mathrm {cf} (\alpha ) < \kappa \}$ . For $\beta < \pi $ with $\mathrm {cf} (\beta ) < \theta $ , let $e_{\beta }$ be the set of all $\xi < \theta $ such that $W_{\xi } \cap \beta $ is stationary in $\beta $ . Note that . Let $C_{\psi }$ be the set of all $x \in P_{\kappa } (\pi )$ such that $\psi (e_{\beta }) < \sup x$ for all $\beta < \sup x$ with $\mathrm {cf} (\beta ) < \theta $ . Strictly speaking, $C_{\psi }$ also depends on the sequence . The reason that this is not reflected in our notation is that in the proofs below, it does not matter which specific sequence we choose. The same remark applies to $W_{\psi }$ and $S_{\psi }$ to be introduced shortly. It is simple to see that $C_{\psi } \in NS_{\kappa , \pi }^{\ast }$ . Let $T_{\psi }$ be the set of all $x \in P_{\kappa } (\pi )$ such that (a) $\sup x \notin x$ , (b) $\sup x = \psi (x)$ , and (c) .

Fact 5.18 [46].

$NS_{\kappa , \theta } = q (NS_{\kappa , \pi })$ , where $q : P_{\kappa } (\pi ) \rightarrow P_{\kappa } (\theta )$ is defined by $q (x) = x \cap \theta $ .

Set $W_{\psi } = \{ x \cap \theta : x \in T_{\psi } \cap C_{\psi } \}$ . Note that by Fact 5.18, if $T_{\psi } \in NS_{\kappa , \pi }^+$ , then $W_{\psi } \in NS_{\kappa , \theta }^+$ .

Observation 5.19. Suppose that ${\cal J}$ is normal, and K is weakly $\pi $ -saturated. Then $W_{\psi } \in K$ .

Proof Suppose otherwise. Then by Observations 5.3, 5.4, and 5.7, we may find $b \in W_{\psi }$ such that:

• • .

• • $\theta> \mathrm {cf} (h (b)) > \vert b \vert $ .

• • $b \subseteq e_{h (b)}$ .

Select $x \in T_{\psi } \cap C_{\psi }$ such that $b = x \cap \theta $ . Then

$$ \begin{align*} \mathrm{cf} (h (b))> \vert b \vert \geq \mathrm{cf} (\sup x) = \mathrm{cf} (\psi (x)) = \mathrm{cf} (\psi (b)), \end{align*} $$

so $h (b) < \psi (b) = \sup x$ . Hence, . Contradiction.

Set . Notice that if $T_{\psi }$ lies in $NS_{\kappa , \pi }^+$ (respectively, $(NG^{\mu }_{\kappa , \pi })^+$ , $(NG^{\mu }_{\kappa , \pi })^{\ast }$ for some regular cardinal $\mu < \kappa $ ), then by Facts 5.18 and 4.5(iii), $S_{\psi }$ lies in (respectively, , ).

Corollary 5.20. Suppose that J is $\theta $ -normal, and $S_{\psi } \in J^{\ast }$ . Then J is not weakly $\pi $ -saturated.

Proof Suppose otherwise. By Observation 5.1, ${\cal J}$ is normal. Moreover, it is weakly $\pi $ -saturated, and by Fact 5.2(iii), so is K. Now clearly, $W_{\psi }$ lies in ${\cal J}^{\ast }$ , and hence in $K^{\ast }$ . This contradicts Observation 5.19.

How large is $S_{\psi }$ ? The following provides some answer.

Observation 5.21. Let $\mu $ be a regular cardinal less than $\kappa $ , and let $q : P_{\kappa } (\pi ) \rightarrow P_{\kappa } (\theta )$ be defined by $q (x) = x \cap \theta $ . Then the following hold:

1. (i) Suppose that $\vert A \vert < \mu $ . Then $S_{\psi }$ lies in $(q (NS_{\mu , \kappa , \pi } \vert \{x : \vert x \vert = \vert x \cap \theta \vert \}))^{\ast }$ (and hence in by Fact 4.5 $(i)$ and $(iii))$ .

2. (ii) Suppose that I is $\mu ^+$ -complete. Then $S_{\psi }$ lies in $(q (N\mu $ - $S_{\kappa ,\pi }))^{\ast }$ (and hence in by Fact 4.5 $(ii)$ and $(iii))$ .

Proof By Observation 4.3.

6 Recapitulation

We have been working so far with a fixed scale ${\vec f}$ . In this brief section we let the scale vary and recapitulate the corresponding results. For this we need to introduce some more members of the large family of $\mathrm {pp}$ functions.

Given two infinite cardinals $\eta $ and $\chi $ such that , and an ideal I on $\eta $ , we put $\mathrm {pp}_I^{\ast }(\chi ) = \sup Y$ , where Y is the set of all cardinals $\pi $ for which one can find a sequence of regular infinite cardinals less than $\chi $ with supremum $\chi $ such that for all $\xi < \chi $ , and $\mathrm {tcf} (\prod _{i < \eta } \chi _i / I ) = \pi $ .

Fact 6.1 (See, e.g., [16, Lemma 9.1.1]).

$\mathrm {pp}_{\sigma } (\chi ) = \sup T$ , where T is the set of all cardinals $\nu $ for which one may find an infinite cardinal and an ideal I on $\eta $ such that $\nu = \mathrm {pp}_I^{\ast }(\chi )$ .

Given three infinite cardinals $\rho $ , $\tau $ , and $\chi $ with , let $\mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$ be the collection of all cardinals $\pi $ such that $\pi = \mathrm {tcf} (\prod A /I )$ for some set A of regular cardinals smaller than $\chi $ with $\vert A \vert < \tau $ and $\sup A = \chi $ , and some $\rho $ -complete ideal I on A with $\{A \cap a : a \in A \} \subseteq I$ . We let $\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ) = \sup \mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$ .

We let $\mathrm {pp}^+_{\Gamma (\tau , \rho )} (\chi )$ equal $(\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ))^+$ if $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi ) \in \mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$ , and $\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi )$ otherwise. Notice that $\mathrm {pp}^+_{\Gamma (\tau , \rho )} (\chi )$ equals $(\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ))^+$ if $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$ is a successor cardinal, and $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$ if $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$ is a singular cardinal.

$\mathrm {pp}_I^{\ast +}(\chi )$ , $\mathrm {pp}^+_{\sigma } (\chi )$ , and $\mathrm {pp}^+ (\chi )$ are defined in the same way.

Proposition 6.2. Suppose that $\kappa $ is a successor cardinal, say $\kappa = \nu ^+$ , and $\theta $ and $\pi $ are two cardinals such that . Then the following hold:

1. (i) Suppose that $\mathrm {cf} (\theta ) < \mathrm {cf} (\nu )$ and $\pi < \mathrm {pp}^+ (\theta )$ . Then there is no $\kappa $ -complete, fine, weakly $\pi $ -saturated ideal on .

2. (ii) Suppose that $\mathrm {cf} (\theta )\not = \mathrm {cf} (\nu )$ and $\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, (\mathrm {cf} (\nu ))^+)} (\theta )$ . Then there is no $\kappa $ -complete, fine, weakly $\pi $ -saturated ideal on .

3. (iii) Suppose that $\mathrm {cf} (\theta ) = \mathrm {cf} (\nu )> \omega $ . Then for any regular cardinal $\mu < \mathrm {cf} (\theta )$ such that $\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, \mu ^+)} (\theta )$ , there is such that no $\theta $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

4. (iv) Suppose that $\mathrm {cf} (\theta ) = \mathrm {cf} (\nu ) < \nu $ and $\pi < \mathrm {pp}^+ (\theta )$ . Then for any regular cardinal $\mu $ with $\mathrm {cf} (\theta ) <\mu < \nu $ , there is such that no $\theta $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

5. (v) Suppose that $\mathrm {cf} (\theta ) = \mathrm {cf} (\nu ) = \omega $ , and $\pi < \mathrm {pp}^{\ast +}_I (\theta )$ for some P-point ideal I on $\omega $ . Then there is such that no $\theta $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

Proof $(i)$ and $(ii)$ : By Theorem 5.15 $(i)$ .

$(iii)$ and $(iv)$ : By Corollary 5.20 and Observation 5.21.

$(v)$ : By Observation 4.7 and Corollary 5.20.

Proposition 6.3. Suppose that $\kappa $ is weakly inaccessible, and $\theta $ and $\pi $ are two cardinals such that . Then the following hold:

1. (i) Suppose that $\pi < \mathrm {pp}^+ (\theta )$ , and let S be the set of all such that $\mathrm {cf} (\vert x \cap \theta \vert )> \mathrm {cf} (\theta )$ . Then no $\theta $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

2. (ii) Suppose that $\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, \tau )} (\theta )$ , where $\tau $ is an uncountable cardinal less than or equal to $\mathrm {cf} (\theta )$ , and let S be the set of all such that $\mathrm {cf} (\vert x \cap \theta \vert ) < \tau $ . Then no $\theta $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

Proof By Theorem 5.15 $(i)$ .

7 More on $\mathrm {pp} (\theta )$ and weak saturation

In this section, we have a closer look at the situation when and describe some cases when no adequate, fine ideal on is weakly $\pi $ -saturated.

Fact 7.1 [31].

Let $\tau $ , $\theta $ , and $\pi $ be three infinite cardinals such that , and let I be an ideal on $\tau $ . Suppose that , and $\pi $ is either singular, or the successor of a regular cardinal. Then there is $k_{\alpha } : \tau \rightarrow \theta $ for $\alpha < \pi $ with the property that for any $e \in P_{\theta ^+} (\pi )$ , there is $g : e \rightarrow I$ such that $k_{\alpha } (i) < k_{\beta } (i)$ whenever $\alpha < \beta $ are in e and $i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$ .

Observation 7.2. Let $\sigma $ , $\theta $ , and $\pi $ be three infinite cardinals such that . Suppose that $\pi $ is either singular, or the successor of a regular cardinal. Then there is $z_{\alpha } \subseteq \theta $ with for with the property that for any $b \in P_{\kappa } (\theta )$ .

Proof Let us first suppose that $\pi $ is the successor of a regular cardinal. By Fact 6.1, we may find an infinite cardinal and an ideal I on $\tau $ such that . By Fact 7.1, there must be $k_{\alpha } : \tau \rightarrow \theta $ for $\alpha < \pi $ with the property that for any $e \in P_{\theta ^+} (\pi )$ , there is $g : e \rightarrow I$ such that $k_{\alpha } (i) < k_{\beta } (i)$ whenever $\alpha < \beta $ are in e and $i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$ . For , let $z_{\alpha } = \{\Phi (i, k_{\alpha } (i)) : i < \tau \}$ (recall that $\Phi $ denotes a one-to-one onto function from $On \times On$ to $On$ such that $\Phi " (\sigma \times \sigma ) = \sigma $ for any infinite cardinal $\sigma $ ). Let $b \in P_{\kappa } (\theta )$ . Assume toward a contradiction that $\vert \{\alpha \in \pi \setminus \theta : z_{\alpha } \subseteq b\} \vert> \vert b \vert $ . Pick $e \subseteq \pi \setminus \theta $ with $\kappa \geq \vert e \vert> \vert b \vert $ such that $\bigcup _{\alpha \in e} z_{\alpha } \subseteq b$ . There must be $g : e \rightarrow I$ such that $k_{\alpha } (i) < k_{\beta } (i)$ whenever $\alpha < \beta $ are in e and $i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$ . For $\alpha \in e$ , select $i_{\alpha }$ in $\tau \setminus g(\alpha )$ . Then the function $s : e \rightarrow b \cap \theta $ defined by $s (\alpha ) = \Phi (i_{\alpha }, k_{\alpha } (i_{\alpha }))$ is one-to-one. Contradiction.

Now suppose that $\pi $ is singular. Pick an increasing sequence of successors of regular cardinals greater than with supremum $\pi $ . For each $j < \mathrm {cf} (\pi )$ , there must be $z^j_{\alpha } \subseteq \theta $ with for with the property that for any $c \in P_{\kappa } (\theta )$ . Hence by Proposition 3.3 of [28], we may find $z_{\alpha } \subseteq \theta $ with for with the property that for any $d \in P_{\kappa } (\theta )$ .

Proposition 7.3. Let $\sigma $ , $\theta $ , and $\pi $ be as in the statement of Observation 7.2, and let J be an adequate (in the sense given to this term in Section 5), fine ideal on . Then J is not weakly $\pi $ -saturated.

Proof We use the isomorphism method of Section 3. Set $H = p (J)$ , where is defined by $p (x) = x \cap \theta $ . By Observation 7.2, there must be $z_{\alpha } \subseteq \theta $ with for so that for any $b \in P_{\kappa } (\theta )$ . Put $z_{\alpha } = \{\alpha \}$ for $\alpha < \theta $ . Define $g : P_{\kappa } (\theta ) \rightarrow P (\pi )$ by $g (b) = \{\alpha < \pi : z_{\alpha } \subseteq b\}$ . Notice that $\vert g (b) \vert = \vert b \vert $ for any $b \in P_{\kappa } (\theta )$ . Now $g (H)$ is an adequate, fine ideal on $P_{\kappa } (\pi )$ , which is not weakly $\pi $ -saturated by Facts 3.1 and 3.2. It follows that H (and hence J) is not weakly $\pi $ -saturated.

Corollary 7.4. Let $\sigma $ , $\theta $ , and $\tau $ be three infinite cardinals such that . Then no adequate, fine ideal on is weakly $\tau $ -saturated.

Proof Apply Proposition 7.3 with $\pi = \tau $ if $\tau $ is singular, and $\pi = \tau ^+$ otherwise.

Proposition 7.3 can also be used to show that weak saturation makes scales short.

Corollary 7.5. Let $\sigma $ , $\theta $ , and $\tau $ be three infinite cardinals such that . Suppose that there exists an adequate, fine, weakly $\tau ^{++}$ -saturated ideal on . Then .

Proof Apply Proposition 7.3 with $\pi = \tau ^{++}$ .

8 More of Usuba

As indicated in its title, [60] is mostly concerned with the case when has small cofinality. However its techniques can also be used in the situation when is regular. Take, for instance, the result of Burke and Matsubara [4] that if is regular and there exists a -saturated, $\kappa $ -complete, fine ideal on , then for each regular cardinal $\mu < \kappa $ , any stationary subset of reflects.

Observation 8.1. Suppose that ( $\kappa $ is weakly inaccessible,) is regular, and J is a weakly -saturated, $\kappa $ -complete, fine ideal on . Then the following hold.

1. (i) Any stationary subset of reflects (and in fact, we can simultaneously reflect less than $\kappa $ many stationary subsets of ).

2. (ii) Suppose that (J is normal or just that) for any $X \in J^+$ and any such that $g (b) < \sup b$ for all $b \in X$ , there is with . Then (that is, for any ), and $(b)$ for any stationary subset T of , the set of all with the property that $T \cap \sup b$ is stationary in $\sup b$ lies in $J^{\ast }$ .

Proof $(i)$ : By Propositions 3.7 and 3.10 of [60], we may find a function

and a $\kappa $ -complete, fine ideal H on

extending J such that

for all

and $(2)$ for any

such that $\{ b : g (b) < k( b) \} \in H^{\ast }$ , there is

with

. It is simple to see that

Now follow the proof of Proposition 4.2 of [60] to establish that , and that of Proposition 4.3 of [60] to establish that for any stationary subset T of , the set of all with the property that $T \cap k (b)$ is stationary in $k (b)$ lies in $H^{\ast }$ .

$(ii)$ : Notice that for all , and for each with the property that for all . Hence by Proposition 3.10 of [60], for any such that $\{ b : g (b) < \sup b \} \in J^{\ast }$ , there is with . Now proceed as in the proof of Proposition 4.2 of [60] for $(a)$ , and as in the proof of Proposition 4.3 of [60] for $(b)$ .

Thus, appealing again to Theorem 2.13 in [15] (see also [11]), if is regular and there exists a weakly -saturated, $\kappa $ -complete, fine ideal on , then fails for every cardinal $\sigma < \kappa $ .

Usuba also proved the following.

Fact 8.2 [59].

Suppose that is regular, and let J be a normal, fine ideal on such that $T \in J^+$ , where T is the set of all such that ( $\sup x$ is an infinite limit ordinal and) x is not stationary in $\sup x$ . Then J is not weakly -saturated.

9 The case when

For the case when is singular of cofinality greater than or equal to $\kappa $ , the following can be used.

Observation 9.1. Suppose that is singular, is an increasing sequence of regular cardinals greater than $\kappa $ with supremum , and J is an ideal on . Suppose further that for any and any $S \in J^+$ , $p_i (J \vert S)$ is not weakly -saturated, where is defined by . Then J is not weakly -saturated.

Proof By our assumption, for any , J is nowhere weakly -saturated. By Fact 1.6 $(i)$ , the desired conclusion follows.

10 Paradise in heaven

Shelah’s Strong Hypothesis (SSH) asserts that $\mathrm {pp}(\chi ) = \chi ^+$ for every singular cardinal $\chi $ .

Shelah [49] (see also [27]) showed SSH to be equivalent to the statement that for any value of $\kappa $ and any value of , equals if , and otherwise.

Large cardinals are needed in order to negate SSH. The exact consistency strength of the failure of SSH is not known, but it is conjectured to be roughly the same as that of the failure of SCH (the Singular Cardinal Hypothesis) that has been shown by Gitik [13] to be equiconsistent with the existence of a measurable cardinal $\chi $ of Mitchell order $\chi ^{++}$ .

On the other hand, just as GCH, SSH may fail everywhere (that is, it is consistent relative to a large large cardinal that $\mathrm {pp} (\sigma )> \sigma ^+$ for every singular cardinal $\sigma $ [38]).

Observation 10.1. Suppose that the following hold:

• • SSH.

• • If $\kappa $ is weakly inaccessible and regular, then there is no normal, fine, precipitous ideal on .

• • If , then holds (or just there is a good scale for ).

Then no normal, fine ideal on is weakly -saturated.

Proof Case when $\kappa $ is a successor and : By Fact 3.1.

Case when $\kappa $ is weakly inaccessible and is regular: Recall that any normal, fine, weakly -saturated ideal on is precipitous.

Case when $\kappa $ is weakly inaccessible and : For any regular cardinal $\chi $ with , we have by (the proof of) the preceding case that no normal, fine ideal on $P_{\kappa } (\chi )$ is weakly $\chi $ -saturated. Now apply Observation 9.1.

Case when : Then , and moreover . Now appeal to Fact 3.8 $(ii)$ if $\kappa $ is a successor, and to Observation 3.14 otherwise.

Corollary 10.2. Suppose that there are no inner models with large cardinals. Then no normal, fine ideal on is weakly -saturated.

Corollary 10.3. Suppose that there are no inner models with large cardinals. Then the following are equivalent:

1. (i) For any values of $\kappa $ and , no normal, fine ideal on is weakly -saturated.

2. (ii) Menas’s conjecture.

3. (iii) for any infinite cardinal $\tau $ .

Proof

1. (i) $\rightarrow \ (\mathrm{ii})$ : Trivial.

2. (ii) $\rightarrow \ (\mathrm{iii})$ : Assume Menas’s conjecture, and let $\tau $ be an infinite cardinal. Set $\kappa = \tau ^+$ and . Then by Observation 1.1,

   
   so .

3. (iii) $\rightarrow \ (\mathrm{i})$ : Assume $(iii)$ . By Corollary 10.2, it suffices to show that for any values of $\kappa $ and , , or equivalently , since . Now if $\kappa $ is a successor, say $\kappa = \tau ^+$ , then . And if $\kappa $ is weakly inaccessible, then

   

SSH is the hard core of GCH, in the sense that [36] GCH = SSH + GCH at regular cardinals (i.e., $2^{\sigma } = \sigma ^+$ for any regular cardinal $\sigma $ (this is the soft part, easily destroyed by forcing $))$ . Thus we would expect SSH to substitute for GCH in many articles in contemporary set-theoretic mathematics. But this is not the case, one possible explanation being that authors are often frightened of pcf theory (who isn’t?). But, to take a similar situation, the fact that they are intimidated by forcing does not prevent researchers to use it in their proofs, encouraged as they are by black box presentations of forcing that make it more accessible. Maybe something analogous should be done for pcf theory.

11 Paradise on earth (but only for the shortsighted)

In this section we show (in ZFC) that if $\kappa $ is greater than $\omega _1$ and close enough to $\kappa $ , then holds. The crucial point is that in this setting, we have, just like under SSH, that if is regular and greater than , then it is the length of some scale. We start with the easier case, when $\kappa $ is a successor cardinal.

For a cardinal k, $FP (k)$ denotes the least fixed point of the aleph function greater than k.

Fact 11.1 [34, Theorem 3.9 and Corollary 3.13].

Suppose that $\kappa $ is a successor cardinal, say $\kappa = \nu ^+$ , and . Then is not a weakly inaccessible cardinal, and moreover there is a cardinal such that:

• • and .

• • .

• • for any cardinal $\chi $ with .

• • .

• • If , then .

Theorem 11.2. Suppose that $\kappa $ is a successor cardinal greater than $\omega _1$ , and . Then holds.

Proof Let $\kappa = \nu ^+$ .

Case when . Then holds, so by Fact 3.1, no $\kappa $ -complete, fine ideal on is weakly -saturated.

Notice that if is a regular cardinal greater than , then by Fact 11.1 it is a successor cardinal.

Case when and is either singular, or the successor of a regular cardinal. Then by Observation 7.2, holds, so by Fact 3.1, no $\kappa $ -complete, fine ideal on is weakly -saturated.

Case when , is the successor of a singular cardinal and . Then by Proposition 6.2 $(i)$ and $(ii)$ , no $\kappa $ -complete, fine ideal on is weakly -saturated.

Case when , is the successor of a singular cardinal, and . Then by Proposition 6.2 $((iv)$ if $\mathrm {cf} (\nu ) = \omega $ , and $(iii)$ and $(iv)$ otherwise), for any regular cardinal , there is such that no -normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Our results are far more modest in the case when $\kappa $ is weakly inaccessible. This is due to our approach in [34] where this case is reduced to the successor case (with the successor cardinal in question being at the first stage $\kappa ^+$ ).

Fact 11.3 [34].

Suppose that $\kappa $ is weakly inaccessible, and let $n < \omega $ . Then the following hold:

1. (i) $u (\kappa , \kappa ^{+(\kappa \cdot n)}) = \kappa ^{+(\kappa \cdot n)}$ .

2. (ii) Suppose that and . Then is a successor cardinal, and moreover .

Theorem 11.4. Suppose that $\kappa $ is weakly inaccessible, and . Then holds.

Proof Let $n < \omega $ be such that .

Case when and is regular. Let S be the set of all such that ( $o.t. (x)$ is an infinite limit ordinal and) either $\mathrm {cf} (o.t. (x)) < o.t. (x)$ , or x is not stationary in $\sup x$ . Then by Facts 3.4 and 8.2, no normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

Case when and . Then . For $i < \kappa $ , set $\alpha _i = \kappa \cdot (n - 1) + i$ and . Put , where $S_i$ is the set of all with the property that $o.t. (a)$ is an infinite limit ordinal such that either $\mathrm {cf} (o.t. (a)) < o.t. (a)$ , or a is not stationary in $\sup a$ .

Claim. .

Proof of the claim

Fix a closed unbounded subset C of . For , set $e_x = \{ i < \kappa : x \setminus \kappa ^{+ \alpha _i} \not = \emptyset \}$ . Inductively define and $c_n \in C$ for $n < \omega $ so that:

• • $x_0 = \omega _1$ .

• • $x_n \subseteq c_n$ .

• • .

Finally, set $x = \bigcup _{n < \omega } x_n$ . The following are readily checked:

• • $x \in C$ .

• • $e_x = x \cap \kappa $ .

• • $x \cap \kappa $ is a limit ordinal of cofinality $\omega $ .

• • $\sup x = \kappa ^{+ \alpha _{x \cap \kappa }}$ .

• • for all $i \in e_x$ .

• • For any $i \in \kappa \setminus e_x$ , (and hence ).

Thus $x \in C \cap S$ , which completes the proof of the claim.

Finally by Observation 9.1, no normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

Case when . Then by Facts 11.1 and 11.3, is a successor cardinal, and moreover , where $\chi $ is the successor cardinal $\kappa ^{+(\kappa \cdot n) + 1}$ . Notice that , so . Let S be the set of all such that . Then by Proposition 6.3, no -normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

To conclude this section we remark that if , is close to $\kappa $ and there are no inner models with large large cardinals, then no normal, fine ideal J on is weakly -saturated.

Observation 11.5. Suppose that , and $\square _{\tau }^{\ast }$ holds for every singular cardinal $\tau $ with . Then the following hold:

1. (i) If $\kappa $ is a successor cardinal, and , then no $\kappa $ -complete, fine ideal on is weakly -saturated.

2. (ii) If $\kappa $ is weakly inaccessible, and , then no normal, fine ideal on is weakly -saturated.

Proof To start with we define $\chi $ by: $\chi $ equals $\kappa $ if $\kappa $ is a successor cardinal, and $\kappa ^{+ (\kappa \cdot n + 1)}$ , where , otherwise. By Fact 11.1 and the proof of Theorem 11.4, the following hold:

• • .

• • .

• • is not a weakly inaccessible cardinal.

Case when is either singular, or the successor of a regular cardinal. Then by Proposition 7.3, we have the following:

• • If $\kappa $ is a successor cardinal, then no $\kappa $ -complete, fine ideal on is weakly -saturated.

• • If $\kappa $ is weakly inaccessible, then no -normal, fine ideal on is weakly -saturated.

Case when is the successor of a singular cardinal $\tau $ . Then for some A and I such that:

• • A is a set of regular cardinals smaller than such that and .

• • I is an ideal on A with $\{A \cap a : a \in A \} \subseteq I$ .

Select an increasing, cofinal sequence $\vec {f}$ in $(\prod A, <_I)$ . We know that $\square _{\tau }^{\ast }$ holds, so by the remark at the end of Section 3.3, the scale $\vec {f}$ is good. Now if $\kappa $ is a successor cardinal, then holds by Fact 3.8 $(ii)$ , and consequently by Fact 3.1, no $\kappa $ -complete, fine ideal on is weakly -saturated. Finally, if $\kappa $ is weakly inaccessible, then by Observation 3.14, no -normal, fine ideal on is weakly -saturated.

12 A poor man’s version

The top-down approach (stating an optimal-looking result and then trying to prove it) did not work so well, so let us see whether we fare better with the bottom-up approach (formulating a result corresponding to the available proofs). We have already seen how to handle the case when . So our starting point is a situation in which and we have a normal, fine ideal J on . The way we see it, our first problem is to produce large disjoint families in $J^+$ . Once this is achieved, it will be time to see whether we can actually find such families of size .

Adding yet a new $\mathrm {pp}$ function to the already long list of existing ones, we let

We let assert the existence of S in with the property that no normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

Given four cardinals $\rho _1, \rho _2, \rho _3, \rho _4$ with $\rho _1 \geq \rho _2 \geq \rho _3 \geq \omega $ and $\rho _3 \geq \rho _4 \geq 2$ , the covering number $\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4)$ denotes the least cardinality of any $X \subseteq P_{\rho _2}(\rho _1)$ such that for any $a \in P_{\rho _3}(\rho _1)$ , there is $Q \in P_{\rho _4}(X)$ with $a \subseteq \bigcup Q$ .

Note that .

Fact 12.1. Let $\tau $ and $\chi $ be two cardinals such that . Then the following hold:

1. (i) [50, 15.7] $\mathrm {cf} (\mathrm {pp}_{\tau } (\chi ))> \tau $ .

2. (ii) [50, Theorem 5.4, p. 87] .

Observation 12.2. .

Proof Let $\tau $ and $\chi $ be two cardinals such that . Then by Fact 12.1 $(ii)$ , .

Thus is a weaker variant of . Too little is known about how and compare. For instance it is tempting to think that if and only if , but we do not know whether this holds.

13 Which way to paradise, please?

In the next section we will attempt to establish that holds for any values of $\kappa $ and , but will fail to do so, and will end up proving something weaker. The case we have trouble with is when , which, we recall, is with $\sigma = \omega $ , is greater than and weakly inaccessible. In the present section we show that, as often in pcf theory, the situation is more manageable when $\sigma $ is uncountable.

Observation 13.1. Let $\theta , k, \rho $ , and $\sigma $ be four cardinals with $\theta \geq k \geq \rho> \sigma = \mathrm {cf} (\sigma ) > \omega $ . Suppose that $\mathrm {cov} (\theta , k, \rho , \sigma )$ is weakly inaccessible and greater than $\theta $ . Then there is a cardinal $\chi $ such that and and a cardinal $\pi \geq \mathrm {cov} (\theta , k, \rho , \sigma )$ such that $\pi \in \mathrm {PP}_{\Gamma (\rho , \sigma )} (\chi )$ .

Proof By [50, Theorem 5.4, pp. 87–88], we may find an infinite cardinal $\tau < \rho $ , a $\sigma $ -complete ideal J on $\tau $ , and a sequence of regular cardinals greater than $\rho $ and less than or equal to $\theta $ , and a cardinal $\pi \geq \mathrm {cov} (\theta , k, \rho , \sigma )$ such that $\pi = \mathrm {tcf}(\prod _{i < \tau } \nu _i /J )$ . Select an increasing, cofinal sequence in $\prod _{i < \tau } \nu _i /J$ .

Let $\chi $ be the least cardinal $\mu $ such that . Note that . Set $e = \{i < \tau : \nu _i = \chi \}$ .

Claim 1. $e \in J$ .

Proof of Claim 1

Suppose otherwise. Then clearly, $\chi $ is regular. For $\alpha < \pi $ , put $\delta _{\alpha } = \sup \{ f_{\alpha } (i) : i \in e \}$ . Note that $\delta _{\alpha } < \chi $ , since . Define $g_{\alpha } : e \rightarrow \chi $ by: $g_{\alpha } (i) = \delta _{\alpha }$ for all $i \in e$ . Since , we may find $\delta < \chi $ and $d \subseteq \pi $ with $\vert d \vert = \pi $ such that $\delta _{\alpha } = \delta $ for all $\alpha \in d$ . Now setting $K = J \vert e$ , is cofinal in $\prod _{i \in e} \nu _i /K$ , and hence so are and . But if we define $k : e \rightarrow \chi $ by: $k (i) = \delta + 1$ for all $i \in e$ , then for all $\alpha \in d$ and all $i \in e$ , $g_{\alpha } (i) < k (i)$ . This contradiction completes the proof of the claim.

Set and $K = J \vert w$ . Then by Lemma 3.1.7 in [16], $\pi = \mathrm {tcf}(\prod _{i \in w} \nu _i /K )$ . Note that by the definition of $\chi $ , $\sup \{ \nu _i : i \in w \} = \chi $ . It follows that . Furthermore, by $\sigma $ -completeness of K.

Put $A = \{ \nu _i : i \in w \}$ , and for each $a \in A$ , $t_a = \{ i \in w : \nu _i = a \}$ . Define $s : w \rightarrow A$ by $s (i) = \nu _i$ , and let $I = s (K)$ . Then clearly, I is a $\sigma $ -complete ideal on A. Note that by the minimality of $\chi $ , $\{A \cap a : a \in A \} \subseteq I$ . Define $G : \prod _{i \in w} \nu _i \rightarrow \prod A$ by: $G (f) (a) = \sup \{ f (i) : i \in t_a \}$ .

Claim 2. Let $r \in \prod A$ . Then there is $u \in \prod _{i \in w} \nu _i$ with the property that $r <_I G (q)$ for any $q \in \prod _{i \in w} \nu _i$ with .

Proof of Claim 2

Define $u \in \prod _{i \in w} \nu _i$ by $u (i) = r (\nu _i) + 1$ . Now fix $q \in \prod _{i \in w} \nu _i$ with . Set and $c = s"b$ . Then $c \in I^{\ast }$ , since $b \in K^{\ast }$ . It is simple to see that $r (a) < G (f) (a)$ for all $a \in c$ . Thus $r <_I G (f)$ , which completes the proof of the claim.

By Lemma 3.1.10 of [16], it follows from Claim 2 that $\mathrm {tcf}(\prod A /I )$ exists and is equal to $\mathrm {tcf}(\prod _{i \in w} \nu _i /K )$ . Thus $\pi \in \mathrm {PP}_{\Gamma (\rho , \sigma )} (\chi )$ .

Observation 13.2. Suppose that is greater than and weakly inaccessible. Then there is such that no normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Proof By Observation 13.1, we may find two cardinals $\chi $ and $\pi $ such that:

• • .

• • .

• • $\pi \in \mathrm {PP}_{\Gamma (\kappa , \omega _1)} (\chi )$ .

Case when $\kappa $ is weakly inaccessible. Put . Then by Corollary 5.16, no $\chi $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

Case when $\kappa $ is a successor cardinal. By Corollary 5.20 and Observation 5.21, there is with the property that no $\chi $ -normal, fine ideal H on with $S \in H^+$ is weakly $\pi $ -saturated.

14 Paradise not found

In this section we establish that holds for many values of $\kappa $ and . We start by computing . We will show that if , then for some cardinal $\theta $ with . We need some facts from pcf theory.

Fact 14.1 [50, Conclusion 2.3(2), p. 57].

Let $\sigma , \tau $ and $\chi $ be three infinite cardinals such that . Then .

Fact 14.2 [34].

Let $\theta $ , A, I, and $\pi $ be such that:

• • $\theta $ is a singular cardinal of cofinality $\omega $ .

• • A is a set of regular cardinals less than $\theta $ with $\sup A = \theta $ and $\vert A \vert < \min A$ .

• • I is an ideal on A with $\{A \cap a : a \in A\} \subseteq I$ .

• • $\mathrm {tcf}(\prod A/I) = \pi $ .

• • $\mathrm {pp}_{\vert A \vert } (\chi ) < \theta $ for any singular cardinal $\chi $ with and $\min A < \chi < \theta $ .

Then $\mathrm {tcf}(\prod B/J) = \pi $ for some countable set B of regular cardinals less than $\theta $ with and $\sup B = \theta $ , and some ideal J on B with $\{B \cap b : b \in B\} \subseteq J$ .

Fact 14.3 [50, Conclusion 1.6(3), p. 321].

Let $\tau $ and $\theta $ be two cardinals such that . Suppose that $\mathrm {pp}_{\tau } (\chi ) < \theta $ for any large enough singular cardinal $\chi < \theta $ with . Then

$$ \begin{align*} \mathrm{pp}_{\tau} (\theta) = \mathrm{pp} (\theta) = \mathrm{pp}_{\Gamma ((\mathrm{cf} (\theta)^+, \mathrm{cf} (\theta))} (\theta) = \mathrm{pp}^{\ast}_{I_{\mathrm{cf}(\theta)}} (\theta). \end{align*} $$

Fact 14.4 [50, Theorem 5.4, pp. 87–88].

Let $\theta , k, \rho $ , and $\sigma $ be four cardinals with $\theta \geq k \geq \rho> \sigma = \mathrm {cf} (\sigma ) > \omega $ . Then

$$ \begin{align*} \max \{\theta, \mathrm{cov} (\theta, k, \rho, \sigma)\} = \max \{\theta, \sup \{ \mathrm{pp}_{\Gamma (\rho, \sigma)} (\chi) : \chi \in Q \}\}, \end{align*} $$

where Q denotes the set of all cardinals $\chi $ such that and .

Observation 14.5. Suppose that . Let be the least cardinal $\chi $ such that for some $\tau $ , and , and let be the least such $\tau $ . Then the following hold:

1. (i) Let $\tau $ and $\chi $ be two cardinals such that and . Then .

2. (ii) Let $\tau $ and $\chi $ be two cardinals such that . Then .

3. (iii) Suppose . Then , , , and for any cardinal $\tau $ with .

4. (iv) Suppose . Then , , , and for any cardinal $\tau $ with .

Proof

1. (i): This follows from Fact 14.1, since .

2. (ii): Suppose otherwise. Then, by Fact 14.1, . Contradiction.

3. (iii): Let us first show that . Suppose otherwise. Then we may find A and I such that:

   • • A is a set of regular infinite cardinals smaller than .

   • • .

   • • $\min A> \kappa $ .

   • • .

   • • I is a prime ideal on A such that $\{A \cap a : a \in A \} \subseteq I$

   • • .

By $(ii)$ , for any singular cardinal $\chi $ with and . Hence, by Fact 14.2, $\mathrm {tcf}(\prod B/J) = \mathrm {tcf}(\prod A /I )$ for some countable set B of regular cardinals less than with and , and some ideal J on B with $\{B \cap b : b \in B\} \subseteq J$ . Contradiction.

Clearly, . By Fact 12.1 $(ii)$ , . Furthermore by $(ii)$ , whenever $\tau $ and $\chi $ are two cardinals such that and .

Claim. Let $\tau $ be a cardinal such that $\omega < \tau < \kappa $ . Then .

Proof of the claim

Suppose otherwise. Then we may find A and I such that:

• • A is a set of regular infinite cardinals smaller than $\theta $ .

• • .

• • $\min A> \kappa $ .

• • $\vert A \vert> \aleph _0$ .

• • I is a prime ideal on A such that $\{A \cap a : a \in A \} \subseteq I$ .

• • .

By $(ii)$ , for any singular cardinal $\chi $ with and . Hence by Fact 14.2, $\mathrm {tcf}(\prod B/J) = \mathrm {tcf}(\prod A /I )$ for some countable set B of regular cardinals less than with and , and some ideal J on B with $\{B \cap b : b \in B\} \subseteq J$ . This contradiction completes the proof of the claim.

Note that by Fact 12.1 $(i)$ , we can deduce from the claim that . Finally, by the claim and $(i)$ , whenever $\tau $ and $\chi $ are two cardinals such that and .

1. (iv): Let $\tau $ be an infinite cardinal less than $\kappa $ . Then for any cardinal $\chi $ such that and . If , then by $(ii)$ and Fact 14.3, .

It follows that , that (by Fact 12.1 $(i))$ , and also (by $(i))$ that for any cardinal $\chi $ such that and . Now suppose that , and $\chi $ is a cardinal such that and . Then . We can now conclude that .

Finally, let Q be the set of all cardinals $\chi $ such that and . Then for any $\chi \in Q$ , . Hence by Fact 14.4, .

Thus

can be defined more simply by

Let us next see how and compare.

Observation 14.6. Suppose that . Then the following hold:

1. (i) Suppose . Then .

2. (ii) Suppose . Then .

Proof It is simple to see that since , .

Claim.

1. (a) Let $\tau $ and $\chi $ be two cardinals such that . Then .

2. (b) Let $\tau $ and $\chi $ be two cardinals such that and . Then .

Proof of the claim

1. (a): By the definition of , .

2. (b): This is immediate from the definition of , which completes the proof of the claim.

Let Q denote the set of all cardinals $\chi $ such that

. By the claim,

for all $\chi \in Q$ . Hence by Fact 14.4,

Now suppose that

. Then

, and consequently

.

Observation 14.7. Suppose that . Then .

Proof Suppose otherwise. Then by Fact 14.4, we may find a cardinal $\chi $ such that and . Hence there must exist a cardinal $\tau $ such that and . But then . Contradiction.

Theorem 14.8.

1. (i) Suppose that either , or is singular, or is the successor of a regular cardinal. Then holds.

2. (ii) Suppose that $\kappa> \omega _1$ , , and either is the successor of a singular cardinal, or is weakly inaccessible and . Then holds.

3. (iii) For any cardinal , no -normal, fine ideal on is weakly $\pi $ -saturated.

Proof $(i)$ and $(ii)$ : Let us first assume that $\kappa $ is a successor cardinal, say $\kappa = \nu ^+$ . The proof is in large part similar to that of Theorem 11.2, so we will skip some details.

Claim 1. Suppose that one of the following holds:

1. (a) .

2. (b) and is either singular, or the successor of a regular cardinal.

3. (c) , is the successor of a singular cardinal and .

4. (d) , is the successor of a singular cardinal, and .

Then no $\kappa $ -complete, fine ideal on is weakly -saturated.

Proof of Claim 1

1. (a): By Fact 3.1, since holds.

2. (b): By Proposition 7.3.

3. (c): By Proposition 6.2 $(i)$ .

4. (d): By Proposition 6.2 $(ii)$ .

This completes the proof of the claim.

Claim 2. Suppose that , is the successor of a singular cardinal, and . Let $\mu $ be a regular cardinal less than $\kappa $ with . Then there is such that no -normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Proof of Claim 2

By Proposition 6.2 $(iv)$ if (note that then $\nu \geq \mu> \mathrm {cf} (\nu )$ , so $\nu $ is singular), and Proposition 6.2 $(iii))$ otherwise.

Claim 3. Suppose that , is weakly inaccessible, and . Then there is such that no normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Proof of Claim 3

By Observation 14.6, . Now apply Observation 13.2. This completes the proof of Claim 3.

Let us now assume that $\kappa $ is weakly inaccessible.

Claim 4.

1. (a) Suppose that and is regular. Let S be the set of all such that ( $o.t. (x)$ is an infinite limit ordinal and) either $\mathrm {cf} (o.t. (x)) < o.t. (x)$ , or x is not stationary in $\sup x$ . Then no normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

2. (b) Suppose that and . Select an increasing sequence of regular cardinals greater than $\kappa $ with supremum , and set , where $S_i$ is the set of all with the property that $o.t. (a)$ is an infinite limit ordinal such that either $\mathrm {cf} (o.t. (a)) < o.t. (a)$ , or a is not stationary in $\sup a$ . Then no normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

Proof of Claim 4

As in the proof of Theorem 11.4.

Claim 5. Suppose that , and is either singular, or the successor of a regular cardinal. Then no -normal, fine ideal on is weakly -saturated.

Proof of Claim 5

By Proposition 7.3.

Claim 6. Suppose that and is the successor of a singular cardinal. Let S be the set of all such that . Then no -normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Proof of Claim 6

Case when . Use Corollary 5.16 $(i)$ .

Case when . By Observation 14.5, . Since is a successor cardinal, we have that

. Now apply Proposition 6.3.

Claim 7. Suppose that , is weakly inaccessible and . Let S be the set of all such that is a singular cardinal of cofinality $\omega $ . Then no normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Proof of Claim 7

By Observation 14.6 and (the proof of) Observation 13.2.

$(iii)$ : By Corollary 7.4.

For models with a singular cardinal $\theta $ such that $\mathrm {pp} (\theta )$ is a weakly inaccessible cardinal, see [14] (note however that in these models, $\mathrm {pp} (\theta )$ is the length of some scale, so that $\mathrm {pp}^+ (\theta ) = (\mathrm {pp} (\theta ))^+$ ).

Theorem 14.8 says little in the case when $\kappa = \omega _1$ , to which we will return in Section 16. Assuming $\kappa> \omega _1$ , the theorem tells us that holds unless is weakly inaccessible and , and even this one case could be claimed to be a near miss, since for any , no normal, fine ideal on is weakly $\pi $ -saturated. However these are mere theoretical considerations. In practice it is not that easy to compute either , or , so Theorem 14.8 is of limited applicability. In this respect the following result, with only one, easy to check, condition, is more appealing.

Theorem 14.9. Suppose that $\kappa> \omega _1$ . Then there is S in with the property that no normal, fine ideal J on with $S \in J^+$ is weakly -saturated.

Proof Case when . Then by Observation 14.7, . Now apply Theorem 14.8 $(i)$ .

Case when . Use Theorem 14.8 $(iii)$ .

Case when and is not weakly inaccessible. Use Theorem 14.8 $(i)$ and $(ii)$ .

Case when and is weakly inaccessible. Use Observation 13.2.

On the other hand, may be quite small. For example, if , then by results of Shelah [50, pp. 86–88], .

Finally, let us compare the results of this section with those of Section 11.

Observation 14.10.

1. (i) Suppose that $\kappa $ is a successor cardinal and (recall that $FP (\kappa )$ denotes the least fixed point of the aleph function greater than $\kappa $ ). Then . Furthermore if , then .

2. (ii) Suppose that $\kappa $ is weakly inaccessible and . Then .

Proof $(i)$ : If

equals

, then so does

by Observation 12.2. Now assume that

. Then by Fact 11.1,

, so

. If this inequality were strict, then setting $\kappa = \nu ^+$ , we would have

Contradiction.

$(ii)$ : If

equals

, then as above so does

. Suppose now that

, and let $n < \omega $ be such that

. Then by definition,

where

and

Now by Fact 11.3 and Observation 12.2,

Furthermore by Facts 11.1 and 11.3,

, so

.

This leaves us confused, since it implies that and are one and the same statement in case is close to $\kappa $ , so that results of this section can be seen as generalizations of those of Section 11. Now is it because we are missing the very last step, which would establish that is always equal to ? Or rather because the general statement should indeed be formulated in terms of which, so to speak by accident, happens to be equal to when is close to $\kappa $ ?

15 Situations when

We have already observed that in the case when , it was not easy to compute , and thus to determine its cofinality (which is crucial for applying Theorem 14.8), or whether it is a fixed point of the aleph function (if it is not, then by a result of Shelah [50, Theorem 2.2, p. 373], cannot be weakly inaccessible). Of course the computation is easy if, for instance, is a strong limit cardinal, or under SSH. In this section we show that there are many situations when . We start by recalling a few facts.

Fact 15.1 [50, pp. 85–86].

Let $\rho _1, \rho _2, \rho _3$ , and $\rho _4$ be four cardinals such that $\rho _1 \geq \rho _2 \geq \rho _3 \geq \omega $ and $\rho _3 \geq \rho _4 \geq 2$ . Then the following hold:

1. (i) $\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4) = \mathrm {cov} (\rho _1, \rho _2, \rho _3, \max \{\omega , \rho _4\})$ .

2. (ii) If $\rho _3> \rho _4 \geq \omega $ , then

   

3. (iii) Suppose that $\rho _3> \mathrm {cf} (\rho _2) \geq \rho _4$ and $\mathrm {cf} (\rho _3) \not = \mathrm {cf} (\rho _2)$ . Then $\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4) = \mathrm {cov} (\rho _1, \rho , \rho _3, \rho _4)$ for some cardinal $\rho $ with $\rho _2> \rho \geq \rho _3$ .

Given a cardinal $\sigma $ and a set Q of regular cardinals, $\sup Q =^+ \sigma $ means that $\sup Q = \sigma $ and moreover either $\sigma \in Q$ , or $\sup Q$ is a singular cardinal.

Fact 15.2 [55, Lemma 18.13], [32].

Assume that:

1. (1) $\theta $ is a cardinal such that $\omega < \mathrm {cf} (\theta ) < \theta $ .

2. (2) is an increasing, continuous sequence of cardinals greater than $\mathrm {cf} (\theta )$ with supremum $\theta $ .

3. (3) $\mathrm {cov} (\theta _i,\theta _i, (\mathrm {cf} (\theta ))^+, 2) < \theta $ for all $i < \mathrm {cf} (\theta )$ .

Then the following hold:

• • $\mathrm {pp} (\theta ) =^+ \mathrm {cov} (\theta , \theta , (\mathrm {cf} (\theta ))^+, 2)$ .

• • $\mathrm {pp}_{I_{\mathrm {cf} (\theta )}}^{\ast }(\theta ) = \mathrm {cov} (\theta ,\theta , (\mathrm {cf} (\theta ))^+, 2))$ .

• • $\{i < \mathrm {cf} (\theta ) : \mathrm {pp}_{I_{\mathrm {cf} (i)}}^{\ast }(\theta _i) = \mathrm {cov} (\theta _i, \theta _i, (\mathrm {cf} (\theta ))^+, 2)\}$ contains a closed unbounded set.

Observation 15.3. Suppose that , and for any cardinal $\tau < \kappa $ and any cardinal $\chi $ with . Then the following hold:

1. (i) .

2. (ii) .

3. (iii) There is a closed unbounded subset D of with the following properties:

   1. (1) D consists of cardinals $\rho $ with $\mathrm {cf} (\rho ) < \kappa < \rho = \theta (\kappa , \rho )$ .

   2. (2) For any $\rho \in D$ , .

Proof

Claim 1. Let $\chi $ be a cardinal such that . Then .

Proof of Claim 1

Let us assume that $\kappa $ is weakly inaccessible, since otherwise the result is trivial. By Fact 15.1,

Now the sequence is nondecreasing, so its supremum must be less than , which completes the proof of Claim 1.

Pick an increasing, continuous sequence of cardinals greater than $\kappa $ with supremum .

Claim 2. There is a closed unbounded subset $C_1$ of with the property that whenever $j < i$ are in $C_1$ .

Proof of Claim 2

Suppose otherwise. Then the set

is stationary, so we may find

and a stationary $W \subseteq T$ such that

for all $i \in W$ with $i> k$ . But then

. This contradiction completes the proof of Claim 2.

Claim 3. There is a stationary subset S of $C_1$ such that for all $k \in S$ .

Proof of Claim 3

By Fact 15.1, for any limit point i of $C_1$ , there is $j < i$ such that . Claim 3 easily follows.

Claim 4. There is a closed unbounded subset $C_2$ of $C_1$ consisting of limit ordinals such that whenever $j < i$ are in $C_2$ and $\chi $ is a cardinal with and $\mathrm {cf} (\chi ) < \kappa $ .

Proof of Claim 4

Let $C_2$ be the set of all limit points of S. Now suppose that $j < i$ are in $C_2$ , and $\chi $ is a cardinal with and $\mathrm {cf} (\chi ) < \kappa $ . There must be $k \in S$ such that . Then , which completes the proof of Claim 4.

Notice that for any $i \in C_2$ , , so .

Claim 5. Let $\tau $ be an infinite cardinal less than $\kappa $ . Then there is $j \in C_2$ such that for each cardinal $\chi $ with and .

Proof of Claim 5

Suppose otherwise, and let $\rho $ be the least cardinal $\chi $ such that , and . By Fact 12.1 $(ii)$ , , so we may find $j \in C_2$ with . Now by Fact 14.1, for each cardinal $\sigma $ with and , . This contradiction completes the proof of the claim.

Claim 6. There is $k \in C_2$ such that for any infinite cardinal $\tau < \kappa $ and any cardinal $\chi $ with and .

Proof of Claim 6

We can assume that $\kappa $ is weakly inaccessible, since otherwise the result is immediate from Claim 5. For each infinite cardinal $\tau < \kappa $ , set $i_{\tau } =$ the least $j \in C_2$ such that for each cardinal $\chi $ with and . Since the sequence is nondecreasing, its supremum k must be less than , which completes the proof of the claim.

Set $C_3 = C_2 \setminus k$ .

Claim 7. Let $i \in C_3$ . Then .

Proof of Claim 7

Let $\tau $ be an infinite cardinal less than $\kappa $ , and let $\chi $ be a cardinal such that

and

. If

, then

. Otherwise, put

and $r = \min (C_2 \setminus (\ell + 1))$ . Then by Fact 12.1 $(ii)$ ,

which completes the proof of Claim 7.

It easily follows from Claim 7 that

. Furthermore by Observation 14.5 and Fact 15.2,

By Fact 15.2, there is a closed unbounded subset $C_4$ of $C_3$ with the property that

for all $i \in C_4$ . Now by Observation 14.5 $(iv)$ , for any $i \in C_4$ of uncountable cofinality,

Finally, given $i \in C_4$ of cofinality $\omega $ , we have by Fact 6.1 that

. Furthermore by Observation 14.5 $(iii)$ ,

Thus, in this case too,

Let us make some comments. First, notice that if and D are as in the statement of Observation 15.3, then by Theorem 14.8, holds, and so does $MC_4 (\kappa , \rho )$ for every $\rho \in D$ of uncountable cofinality. Furthermore if is not a fixed point of the aleph function, then for any large enough $\rho $ in D (of cofinality $\omega $ ), ( $\rho $ is not a fixed point of the aleph function and) $\mathrm {pp}_{I_{\mathrm {cf} (\rho )}}^{\ast }(\rho )$ is not weakly inaccessible, and hence $MC_4 (\kappa , \rho )$ holds. Notice further that if in the statement of the observation, we make the stronger assumption that for any cardinal , then we may find a closed unbounded subset $D'$ of D such that $\chi ^{< \kappa } < \rho $ whenever $\rho \in D'$ and $\chi $ is a cardinal less than $\rho $ . Now by results of Shelah (see, e.g., Theorems 9.1.2 and 9.1.3 in [16]), if $\tau $ and $\sigma $ are two cardinals such that , $(b) \ \chi ^{\tau } < \sigma $ for any cardinal $\chi < \sigma $ , and $(c)$ either $\mathrm {cf} (\sigma )> \omega $ , or $\sigma $ is not a fixed point of the aleph function, then $\mathrm {pp}_{\tau } (\sigma ) = \sigma ^{\tau }$ . Hence for any , $(a) \ \mathrm {pp} (\kappa , \sigma ) = \sigma ^{< \kappa } = u (\kappa , \sigma )$ and $(b) \ MC_3 (\kappa , \sigma )$ holds if $\mathrm {cf} (\sigma )> \omega $ . Moreover if is not a fixed point of the aleph function, then $MC_3 (\kappa , \sigma )$ holds for any large enough $\sigma $ in $D'$ (of cofinality $\omega $ ).

16 The case $\kappa = \omega _1$

What is so special about the case $\kappa = \omega _1$ is that there is only one possible cofinality (for, e.g., ), namely $\omega $ , which is thus unavoidable.

As we have seen, one problem we have to deal with for any value of $\kappa $ is the possibility of the weak inaccessibility of (with ). For $\kappa = \omega _1$ , we may appeal to Theorem 14.8 $(i)$ and $(iii)$ . Further, Observation 4.7 and Corollary 5.20 give us the following.

Observation 16.1. Suppose that $(a) \ \kappa = \omega _1$ , , is the successor of a singular cardinal, and for some P-point ideal I on $\omega $ . Then holds, and in fact there is such that no -normal, fine ideal H on with $S \in H^+$ is weakly -saturated.

Here we have a second problem, due to the P-pointness condition. It turns out that if is close to $\kappa $ , this condition can be removed. Recall that the pseudointersection number $\frak {p}$ is the least size of any collection Z of infinite subsets of $\omega $ such that $(a) \ \vert \bigcap w \vert = \aleph _0$ for any $w \subseteq Z$ with $0 < \vert w \vert < \aleph _0$ , and $(b)$ there is no infinite $A \subseteq \omega $ such that $\vert A \setminus B \vert < \aleph _0$ for all $B \in Z$ . The following, which was pointed out to the author by Todd Eisworth, is largely due to Shelah (see [50, Remark 1.6B, p. 322] and [52]).

Fact 16.2 [32].

Let $\theta $ and $\pi $ be two infinite cardinals such that $\omega = \mathrm {cf}(\theta ) < \theta < \pi = \mathrm {cf}( \pi ) < \min (\mathrm {pp}^+(\theta ), \theta ^{+ \frak {p}})$ . Then there is a set u of regular cardinals such that $\sup u = \theta $ , $\vert u \vert = \aleph _0 < \min u$ and $\mathrm {tcf} (\prod u / I_u) = \pi $ .

Observation 16.3. Suppose that $\kappa = \omega _1$ and . Then holds.

Proof Case when . Then by Fact 3.1, no $\kappa $ -complete, fine ideal on is weakly -saturated.

Case when . By Observation 14.10 $(i)$ , (and hence and assert the same thing). Furthermore by Fact 11.1, is not weakly inaccessible. Now holds by Observation 16.1 and Fact 16.2 if is the successor of a singular cardinal, and by Theorem 14.8 $(i)$ otherwise.

17 A small, private, devotional altar to pcf theory

The original conjecture of Menas is not only consistently false, by the result of Baumgartner and Taylor [3], but it is also, as seen in Corollary 10.3, heavily dependent on cardinal arithmetic. A weaker statement, which looks more reasonable, asserts that the nonstationary ideal is nowhere weakly -saturated (where denotes the least size of any cofinal subset of ), but by the result of Gitik [12], this assertion too is relative to a (large) large cardinal, consistently false. If there are no large cardinals in an inner model, and either , or is the successor of a singular cardinal of cofinality less than $\kappa $ , the assertion does hold by Observation 10.1 and Proposition 3.8, and in fact no normal, fine ideal on is weakly -saturated (so, contrary to Gitik, we are not taking advantage of the specificity of ). By Facts 3.4 and 8.2, and Observations 8.1 and 10.1, a similar result holds in the case when ( $\kappa $ is weakly inaccessible,) (and is not the successor of a cardinal of cofinality less than $\kappa $ ). However with such statements we are far from the (unconditional) spirit of Menas’s conjecture. So how much of the original conjecture is true in ZFC? By Theorems 11.2 and 11.4, if $\kappa> \omega _1$ and is close to $\kappa $ , then there is such that no normal extension of is weakly -saturated. This can be generalized to some extent. If $\kappa> \omega _1$ and is not weakly inaccessible (where ), then by Theorem 14.8, there is such that no normal extension of is weakly -saturated. Much remains to be clarified. What about the case when $\kappa = \omega _1$ ? Is it consistent that ? That is weakly inaccessible and greater than ?

There are problems that are intractable in ZFC alone, but have a shadow version that can be established using the tools of pcf theory. Some people are not impressed, pointing out that the original problems remain unresolved. For others it is a way of showing that ZFC is not so desperately incomplete as it may seem. The most prominent such problem is the Generalized Continuum Hypothesis revisited by Shelah in [51]. Our goal in the present paper was to show, on a more modest scale, that Menas’s Conjecture is also amenable to an analysis of this type. Hopefully, future will tell which is the correct formulation for its shadow variant: should it be , or maybe some other assertion?