Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T01:58:54.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperclassical Logic (A.K.A. If Logic) and its Implications for Logical Theory

Published online by Cambridge University Press:  15 January 2014

Jaakko Hintikka
Jaakko Hintikka*
Affiliation:
Department of Philosophy, Boston University, 745 Commonwealth Ave., Boston, MA 02215, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Let us assume that you are entrusted by UNESCO with an important task. You are asked to devise a universal logical language, a Begriffsschrift in Frege's sense, which is to serve the purposes of science, business and everyday life. What requirements should such a “conceptual notation” satisfy? There are undoubtedly many relevant desiderata, but here I am focusing on one unmistakable one. In order to be a viable lingua universalis, your language must in any case be capable of representing any possible configuration of dependence and independence between different variables. For if such a configuration is possible in principle, there is no guarantee that it might not one day show up among the natural, human or social phenomena we have to study.

But how are dependencies and independencies between variables expressed in our familiar logical notation? Every logician worth his or her truth-table knows the answer. Dependencies between two variables are expressed by dependencies between the quantifiers to which they are bound. For instance, in

the variable y depends on x, while in

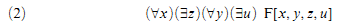
z depends on x but not on y, while u depends on both x and y.

But how is the dependence of a quantifier on another one expressed in familiar logical languages? Obviously by occurring in its scope, indicated by the pair of parentheses following it (cf. here Hintikka [1997]). But the nesting of scopes is a transitive and antisymmetrical relation which allows branching only in one direction. Hence other kinds of structures of dependence and independence between variables are not representable in the received logical notation. Such previously inexpressible structures form the subject matter of what has been referred to as independence-friendly (IF) logic.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 8 , Issue 3 , September 2002 , pp. 404 - 423
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barwise, Jon [1979], On branching quantifiers in English, Journal of Philosophical Logic, vol. 8, pp. 47–80.Google Scholar
Cameron, Peter and Hodges, Wilfrid [forthcoming], Some combinatorics of imperfect information .Google Scholar
Dirac, Paul [1964], Lectures on quantum mechanics, Yeshiva University, New York, (reprinted, Dover 2001.).Google Scholar
Enderton, H.B. [1970], Finite partially ordered quantifiers, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 16, pp. 393–397.Google Scholar
Henkin, Leon [1961], Some remarks on infinitely long formulas, Infinitistic methods, Pergamon Press, Oxford, pp. 167–183.Google Scholar
Hintikka, Jaakko [1996], The principles of mathematics revisited, Cambridge University Press.CrossRefGoogle Scholar
Hintikka, Jaakko [1997], No scope for scope?, Linguistics and Philosophy, vol. 20, pp. 515–544.Google Scholar
Hintikka, Jaakko [forthcoming (a)], The problem of quantization and independence-friendly logic .Google Scholar
Hintikka, Jaakko [forthcoming (b)], Negation in logic and in natural language, Linguistics and Philosophy .Google Scholar
Hintikka, Jaakko [forthcoming (c)], Reply to van Benthem, The Philosophy ofJaakko Hintikka (Library of Living Philosophers) (Hahn, Lewis and Auxier, Randall, editors), Open Court, La Salle, Illinois.Google Scholar
Hintikka, Jaakko and Sandu, Gabriel [1996], Game-theoretical semantics, Handbook of logic and language (van Benthem, J. and ter Meulen, Alice, editors), Elsevier, Amsterdam, pp. 361–410.Google Scholar
Hodges, Wilfrid [1997 (a)], Compositional semantics for a language of imperfect information, Logic Journal of the Interest Group in Pure and Applied Logics, vol. 5, pp. 539–563.Google Scholar
Hodges, Wilfrid [1997 (b)], Some strange quantifiers, Lecture notes in computer science (Myclielski, J. et al., editors), vol. 1261, Springer-Verlag, Berlin, pp. 51–65.Google Scholar
Hodges, Wilfrid [forthcoming], The logic of quantifiers, The Philosophy of Jaakko Hintikka (Library of Living Philosophers) (Hahn, Lewis and Auxier, Randall, editors), Open Court, La Salle, Illinois.Google Scholar
Tennant, Neil [1998], Games some people would have all of us play, Philosophia Mathematica, vol. 6, pp. 90–115.CrossRefGoogle Scholar
Walkoe, W. Jr. [1970], Finite partially ordered quantification, The Journal of Symbolic Logic, vol. 35, pp. 535–555.Google Scholar