Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T00:58:39.804Z Has data issue: false hasContentIssue false
  • English
  • Français

New Dichotomies for Borel Equivalence Relations

Published online by Cambridge University Press:  15 January 2014

Greg Hjorth  and
Alexander S. Kechris
Greg Hjorth
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095, USAE-mail: [email protected]
Alexander S. Kechris
Affiliation:
Department of Mathematics, California Institute of Technology, Pasadena, CA 91125, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We announce two new dichotomy theorems for Borel equivalence relations, and present the results in context by giving an overview of related recent developments.

§1. Introduction. For X a Polish (i.e., separable, completely metrizable) space and E a Borel equivalence relation on X, a (complete) classification of X up to E-equivalence consists of finding a set of invariants I and a map c : X → I such that xEy ⇔ c(x) = c(y). To be of any value we would expect I and c to be “explicit” or “definable”. The theory of Borel equivalence relations investigates the nature of possible invariants and provides a hierarchy of notions of classification.

The following partial (pre-)ordering is fundamental in organizing this study. Given equivalence relations E and F on X and Y, resp., we say that E can be Borel reduced to F, in symbols

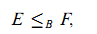
if there is a Borel map f : X → Y with xEy ⇔ f(x)Ff(y). Then if is an embedding of X/E into Y/F, which is “Borel” (in the sense that it has a Borel lifting).

Intuitively, E ≤BF might be interpreted in any one of the following ways:

(i) The classi.cation problem for E is simpler than (or can be reduced to) that of F: any invariants for F work as well for E (after composing by an f as above).

(ii) One can classify E by using as invariants F-equivalence classes.

(iii) The quotient space X/E has “Borel cardinality” less than or equal to that of Y/F, in the sense that there is a “Borel” embedding of X/E into Y/F.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 3 , Issue 3 , September 1997 , pp. 329 - 346
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1975] Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin.CrossRefGoogle Scholar
[1996] Becker, H. and Kechris, A. S., The descriptive set theory of Polish group actions, London Mathematical Society Lecture Notes, vol. 232, Cambridge University Press, Cambridge.Google Scholar
[1994] Dougherty, R., Jackson, S., and Kechris, A. S., The structure of hyperfinite Borel equivalence relations, Transactions of the American Mathematical Society, vol. 341, no. 1, pp. 193–225.CrossRefGoogle Scholar
[1977] Feldman, J. and Moore, C. C., Ergodic equivalence relations, cohomology and von Neumann algebras, I, Transactions of the American Mathematical Society, vol. 234, pp. 289–324.Google Scholar
[1990] Harrington, L., Kechris, A. S., and Louveau, A., A Glimm-Effros dichotomy for Borel equivalence relations, Journal of the American Mathematical Society, no. 4, pp. 903–927.Google Scholar
[1995] Hjorth, G., Actions of S∞ , circulated notes.Google Scholar
[1996], Actions by the classical Banach spaces, preprint.Google Scholar
[1996] Hjorth, G. and Kechris, A. S., Borel equivalence relations and classifications of countable models, Annals of Pure and Applied Logic, vol. 82, pp. 221–272.CrossRefGoogle Scholar
[1996] Hjorth, G., Kechris, A. S., and Louveau, A., Borel equivalence relations induced by actions of the symmetric group, preprint.Google Scholar
[∞] Jackson, S., Kechris, A. S., and Louveau, A., On countable Borel equivalence relations, to appear.Google Scholar
[1991] Kechris, A. S., Amenable equivalence relations and Turing degrees, Journal of Symbolic Logic, vol. 56, pp. 182–194.Google Scholar
[1992] Kechris, A. S., Countable sections for locally compact group actions, Ergodic Theory and Dynamical Systems, vol. 12, pp. 283–295.CrossRefGoogle Scholar
[1994] Kechris, A. S., Lectures on definable group actions and equivalence relations, preprint.Google Scholar
[1995] Kechris, A. S., Classical descriptive set theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York.CrossRefGoogle Scholar
[1996] Kechris, A. S., Rigidity properties of Borel ideals on the integers, preprint.Google Scholar
[1996a] Kechris, A. S., Notes on turbulence, preprint.Google Scholar
[1997] Kechris, A. S. and Louveau, A., The structure of hypersmooth Borel equivalence relations, Journal of the American Mathematical Society, vol. 10, no. 1, pp. 215–242.Google Scholar
[1994] Louveau, A., On the reducibility order between Borel equivalence relations, Studies in logic and the foundations of mathematics, vol. 134, North-Holland, pp. 151–155.Google Scholar
[1994] Louveau, A. and Velickovic, B., A note on Borel equivalence relations, Proceedings of the American Mathematical Society, vol. 120, pp. 255–259.CrossRefGoogle Scholar
[1996] Mazur, K., A modification of Louveau and Velickovic construction for Fσ ideals , preprint.Google Scholar
[1980] Silver, J. H., Counting the number of equivalence classes of Borel and coanalytic equivalence relations, Annals of Mathematical Logic, vol. 18, pp. 1–28.Google Scholar
[1996] Solecki, S., Analytic ideals, this Journal, vol. 2, no. 3, pp. 339–348.Google Scholar