Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T07:22:05.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Solution of general inhomogeneous linear difference equations

Published online by Cambridge University Press:  17 February 2009

H. Van Hoa
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The general solution of the rth inhomogeneous linear difference equation is given in the form

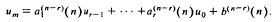
The coefficients 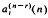, i = 2, …, r, and b(n−r)(n) can be evaluated from n values 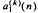, k = 0, …, n − 1, which santisfy an rth order homogenous linear difference equation. In the rth order homogeneous case and if n ≥ 2r, the method requires the evaluation of r determinants of successive orders n − 2r + 1, n − 2r + 2, …, n − r. If r ≤ n ≤ 2r − 1, only n − r determinants are required, with orders varying from 1 to n − r. In the second order ihnomogenous case, 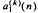can be evaluated from a continued fraction amd a simple product.

Type
Research Article
Information
The ANZIAM Journal , Volume 24 , Issue 4 , April 1983 , pp. 466 - 472
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Brown, A., “Solution of a linear difference equation”, Bull. Austral. Math. Soc. 11 (1974), 325–331.CrossRefGoogle Scholar
[2]Love, J. D., “Solution of homogeneous linear difference equations”, J. Austral. Math. Soc. Ser. B 21 (1980), 293–296.CrossRefGoogle Scholar
[3]Singh, V. N., “Solution of a general homogeneous linear difference equation”, J. Austral. Math. Soc. Ser. B 22 (1980), 53–57.CrossRefGoogle Scholar