Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zayed, E. M. E.
1989.
Heat equation for an arbitrary doubly-connected region inR 2 with mixed boundary conditions.
ZAMP Zeitschrift f�r angewandte Mathematik und Physik,
Vol. 40,
Issue. 3,
p.
339.
Zayed, E. M. E.
1990.
On hearing the shape of an arbitrary doubly-connected region in R2.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 31,
Issue. 4,
p.
472.
Zayed, E. M. E.
and
Younis, A. I.
1994.
On hearing the shape of rectilinear regions.
Journal of Mathematical Physics,
Vol. 35,
Issue. 7,
p.
3490.
Zayed, E.M.E.
and
Abdel-Halim, I.H.
2001.
The 3D inverse problem for waves with fractal and general annular bounded domain with piecewise smooth Robin boundary.
Chaos, Solitons & Fractals,
Vol. 12,
Issue. 12,
p.
2307.
Zayed, E.M.E.
and
Abdel-Halim, I.H.
2001.
The wave equation approach to the two-dimensional inverse problem for a general bounded domain with piecewise smooth mixed boundary conditions.
Acta Mathematica Scientia,
Vol. 21,
Issue. 2,
p.
171.
Zayed, E.M.E.
and
Abdel-Halim, I.H.
2002.
An inverse problem of the wave equation for a general doubly connected region in with a finite number of piecewise smooth Robin boundary conditions.
Applied Mathematics and Computation,
Vol. 132,
Issue. 1,
p.
187.
Zayed, E.M.E.
2003.
The wave equation approach to an inverse problem for a general multi-connected domain in R2 with mixed boundary conditions.
Applied Mathematics and Computation,
Vol. 144,
Issue. 2-3,
p.
457.
Zayed, E.M.E.
2003.
On hearing the shape of a general multi-connected vibrating membrane in with piecewise smooth positive functions in the Robin boundary conditions.
Applied Mathematics and Computation,
Vol. 135,
Issue. 2-3,
p.
361.


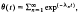 , where
, where 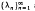 are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(
are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(