INTRODUCTION
In mesoscale numerical weather prediction (NWP) models, sea-ice cover is typically represented by grid-cell-averaged ice concentration and thickness. Relevant surface variables – surface heat and moisture flux, roughness, albedo and so on – are calculated as a weighted average of the respective values over sea ice and open water. With typical model resolutions of a few kilometres, all smaller-scale variability related to the nonuniform spatial distribution of sea ice within model grid cells cannot be taken into account. As the larger-scale effects of these submesoscale processes are largely unknown, no parametrizations suitable for NWP models are available. Although the effects of different sizes and distributions of leads have been previously studied (Pinto and others, Reference Pinto, Curry and McInnes1995; Alam and Curry, Reference Alam and Curry1997; Gultepe and others, Reference Gultepe, Isaac, Williams, Marcotte and Strawbridge2003), the significance of the size distribution and spatial arrangement of sea-ice floes has only recently received attention (Horvat and others, Reference Horvat, Tziperman and Campin2016), but with a focus more on the oceanic boundary layer than on the ABL. Nevertheless, there is growing observational and theoretical evidence that floe-level processes have significant influence on the dynamics and thermodynamics of the lower atmosphere and upper ocean, as well as the ice cover itself.
The presence of cracks and leads in the sea-ice cover considerably influences both the atmosphere and oceanic boundary layer. In winter, the air/sea temperature difference can reach 20–30 K, generating a major shift in the exchange of heat and moisture and resulting in a notable increase in the turbulent fluxes (Andreas, Reference Andreas1980). Although the emission of heat directly from the leads is partially balanced by opposite (negative) fluxes over pack ice (Overland and others, Reference Overland2000), the fractures still have considerable influence on the atmospheric conditions (Lümlpkes and others, Reference Lümlpkes2008a).
Where there are large air/sea temperature gradients, large changes in convective heat transfer (Andreas and Cash, Reference Andreas and Cash1999) and thus in the atmospheric circulation have been observed above the ice cover (Alam and Curry, Reference Alam and Curry1995). Large Eddy Simulation (LES) modeling results over the fragmented sea ice indicate that strong convective heat transport from leads can have a stabilizing effect on the atmospheric boundary layer (ABL) structure downstream of leads (Lümlpkes and others, Reference Lümlpkes2008a) and that its influence is noticeable not only locally, but on a regional scale as well (Tetzlaff and others, Reference Tetzlaff, Lümlpkes and Hartmann2015). The structure and strength of convection is strongly influenced by prevailing wind conditions (Alam and Curry, Reference Alam and Curry1995; Ruffieux and others, Reference Ruffieux, Persson, Fairall and Wolfe1995), as well as ABL stability (Tetzlaff and others, Reference Tetzlaff, Lümlpkes and Hartmann2015). The relatively warm surface of the open water can initiate thermal eddies (Glendening and Burk, Reference Glendening and Burk1992). They are generated as a result of thermal updrafts related to the large air/sea temperature difference above the lead, and accelerate vertically until losing their excess buoyancy. However, maximum eddy generation occurs over a lead when the thermal eddy development time is shorter than its horizontal advection away from the lead. When this condition is met , thermal eddies are then mostly observed downwind of narrow leads (Glendening and Burk, Reference Glendening and Burk1992; Ruffieux and others, Reference Ruffieux, Persson, Fairall and Wolfe1995).
Another effect of buoyancy flux release is the formation of steam fog and cloud plumes (Burk and others, Reference Burk, Fett and Englebretson1997), observed on satellite images (Fett and others, Reference Fett, Burk, Thompson and Kozo1994). It has been found that steam fog tends to dissipate quickly directly above the lead, while the elevated cloud plume of usually mixed phase (water and ice) usually extends further downwind of the lead (Fett and others, Reference Fett, Burk, Thompson and Kozo1994; Burk and others, Reference Burk, Fett and Englebretson1997). When the background atmosphere is stably stratified, the plume penetrating ABL can also generate gravity waves (Mauritsen and others, Reference Mauritsen, Svensson and Grisogono2005). The development of cloud plume above and downwind of the lead is determined, most of all, by ABL stability and lead width (Burk and others, Reference Burk, Fett and Englebretson1997). Furthermore, the boundary layer response gets weaker with increasing lead width; as the lead width decreases, the surface turbulent fluxes increase (Marcq and Weiss, Reference Marcq and Weiss2012). Narrow leads (several meters wide) are thus two times more efficient at transmitting turbulent heat than leads reaching several hundreds of meters (Marcq and Weiss, Reference Marcq and Weiss2012) and have a stronger overall effect on atmospheric processes mentioned above. Andreas and Cash (Reference Andreas and Cash1999) associated such results with the combined influence of forced and free convection. Nonetheless, when the flux measurements were performed directly over the leads, turbulent heat fluxes (THFs) were stronger over leads hundreds of meters wide than over an assemblage of narrow ones (Winter Arctic Polynya Study; Lümlpkes and others, Reference Lümlpkes2012b). As Marcq and Weiss (Reference Marcq and Weiss2012) observed, such leads should be considered as an open ocean, since the overlying heat fluxes are not dependent on the lead width. On the other hand, Tetzlaff (Reference Tetzlaff2016) pointed out that the intensity of turbulent fluxes varies significantly with the value of wind fetch, therefore making the comparison of different studies problematic.
Considering the complexity of the impact of leads on the ABL, Lümlpkes and others (Reference Lümlpkes2008a) used microscale modeling of air flow over leads to analyze the development of turbulence closure. Such studies provide additional insight into the governing processes related to the atmospheric response to fragmented sea ice. As the characteristics of plumes forming over leads depend on lead width, lead ice cover, wind speed, upstream stratification of the ABL and the inversion strength (Alam and Curry, Reference Alam and Curry1995; Glendening, Reference Glendening1995; Zulauf and Krueger, Reference Zulauf and Krueger2003b), the NWP models should take into account their combined influence. Lümlpkes and others (Reference Lümlpkes2008a) found that this is problematic even in high-resolution model simulations, theoretically capable of resolving even narrow leads, since their grid sizes are usually still too large to resolve the complicated structure of convective plumes.
Keeping in mind the significant influence of open water presence and spatial distribution of leads (as discussed above), we can expect similar results for fragmented sea-ice cover with various floe size distributions as is typical for the marginal ice zone (MIZ). However, very few studies have taken this topic into consideration. In a numerical study of the surface ocean circulation around rectangular ice floes of different sizes, Horvat and others (Reference Horvat, Tziperman and Campin2016) demonstrated that from thermodynamical effects related to heat flux gradients at floe boundaries, eddies can form, and through a number of feedbacks, melt rates change with changing floe size distribution within the model area. Although these results are based on idealized model simulations, they clearly demonstrate the significance of atmosphere/sea ice/ocean interactions and boundary layer processes over fragmented nonuniform sea ice. To the best of our knowledge, similar studies on the influence of the floes size distributions on the ABL have not yet been conducted.
In this work, in view of the scarcity of studies devoted to floe-related atmospheric processes, a number of high-resolution simulations were conducted with the Weather Research and Forecasting (WRF) model for different floe-size distributions. Furthermore, to study the atmospheric response over leads of various widths and spatial arrangements, the model was also run with several different lead configurations. Since this analysis is based on an idealized model setup, some of the processes and features of the ABL are simplified and values of certain variables might be over- or underestimated. This is especially true for local, instantaneous values which are extremely sensitive to surface heterogeneities. In our analysis, we focus mainly on the domain-averaged characteristics of the ABL, which are more robust and, importantly, in agreement with results of other studies. Due to the idealized character of our study, we neither intent to reproduce any specific event or dataset from the polar region, nor to make direct comparisons with the specific observational dataset. We analyse the three-dimensional structure of the atmospheric circulation, atmospheric moisture content, surface heat flux, as well as the influence of small-scale atmospheric variability on domain-averaged properties of the ABL. The main result of this paper is that the domain-averaged values are sensitive not only to sea-ice concentration, but also to the subgrid-scale spatial distribution of sea ice. This suggests that parametrizing these effects should lead to improved performance of the NWP models over fragmented sea ice.
The simulations in this study are performed for atmospheric conditions observed at the Surface Heat Budget of the Arctic Ocean (SHEBA) ice camp on a selected winter day (Uttal and others, Reference Uttal2002). In this context, it is worth stressing that the sea-ice features considered here – fractures in the form of leads, as well as ice floes with a wide range of sizes – are not only associated with the melt season, but they also appear regularly in the Arctic during winter, especially in the last decades, as the ice cover became thinner and more susceptible to drift and deformation. Particularly, the sea ice in the Beaufort Sea is frequently fragmented by strong winter storms (Hudak and Young, Reference Hudak and Young2002). Intense cyclones can extensively fracture the sea ice over very large areas, creating multiple leads (Fig. 1a); close to the shores and in straits, small floes with power-law size distributions are common (Figs. 1a and b). Those fractures are very often almost instantaneously covered by thin, new sea ice, which limits the heat, moisture and momentum exchange between open water and overlying atmosphere. However, although lower than over open water, the surface fluxes through refrozen leads are still significantly enhanced for extended periods of time (Ruffieux and others, Reference Ruffieux, Persson, Fairall and Wolfe1995; Alam and Curry, Reference Alam and Curry1997). Furthermore, the refreezing rates over leads are nonuniform and strongly depend on prevailing wind conditions; a strong wind can result in the piling up of new sea ice, thus prolonging the presence of open water (Alam and Curry, Reference Alam and Curry1998). Thus, the results presented in this paper can be considered realistic only on short time scales (several hours), as the freeze-up processes are not included in the WRF model configuration. The thicker the new ice between ice floes, the smaller the spatial variability of surface fluxes, and the weaker the resulting response of the ABL.
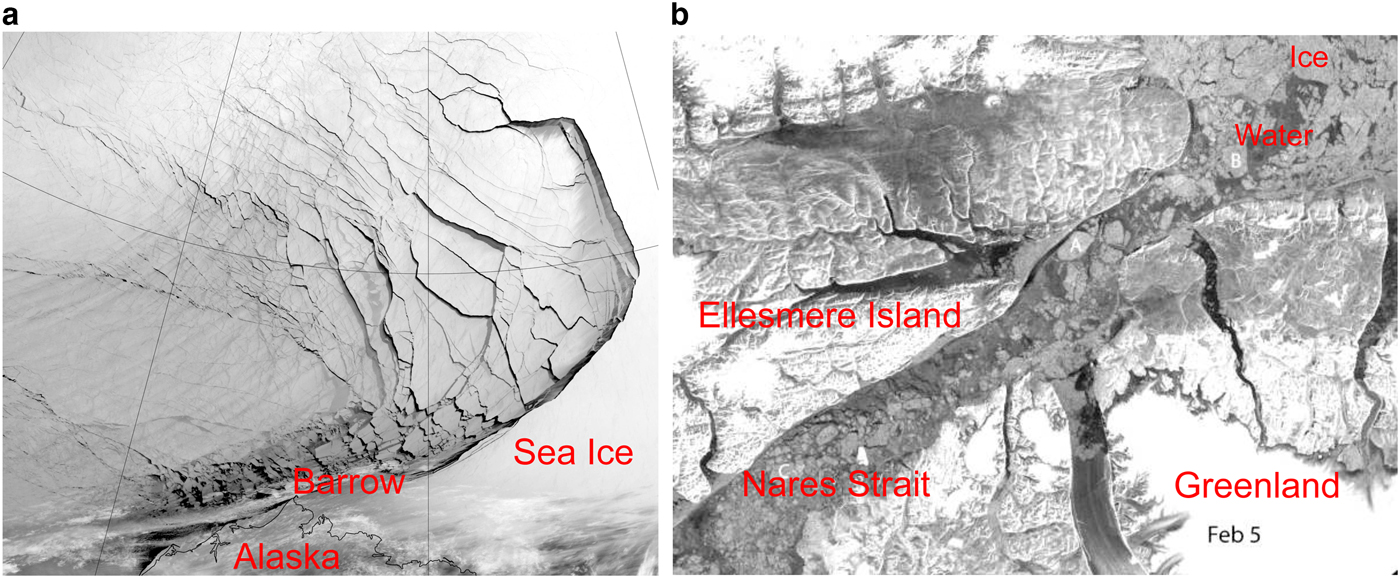
Fig. 1. (a): Extensive sea-ice fracturing off the northern coast of Alaska, captured by Visible Infrared Imaging Radiometer Suite (VIIRS) on the Suomi NPP satellite, 23 February 2013; (b): Sea-ice fractures in the Nares Strait (Kane basin), Sentinel-1, ESA (via DMI Centre for Ocean and Ice), 5 February 2015. Dark areas in the images may represent open water or newly formed, thin sea ice.
MODEL CONFIGURATION
In the present study, version 3.8.1 (August 2016) of the Advanced Research WRF (ARW) model is used in the so-called ‘idealized case mode’. In this class of WRF simulations, a single sounding consisting of the vertical profiles of potential temperature (K), water vapor mixing ratio (g kg−1), U (west–east) velocity (m s−1) and V (south–north) velocity (m s−1) is used to initialize the model. The full air pressure and density, as well as other variables, are computed from the input sounding. The thermodynamic reference state is calculated on the basis of the input sounding without moisture. Thereafter, the dry column pressure (μ d) is computed, the vertical model grid (so-called η-levels) is initialized and all relevant variables are interpolated to η-levels. Values of air density, geopotential height and μ d are computed assuming the atmosphere is in a hydrostatic balance. The atmospheric pressure and wind speed are initially horizontally uniform over the whole model domain and they are allowed to freely evolve during a simulation. There is no geostrophic wind prescribed. Consequently, inertial oscillations develop in the simulations with nonzero ambient wind conditions. This aspect of the model setup is undoubtedly unrealistic. However, the analyzed quantities are not significantly affected, as the inertial period is large compared with the timescales characterizing the local, small-scale circulation associated with the surface inhomogeneities. A similar approach is often adopted in LES studies (e.g. Vihma and others, Reference Vihma, Tuovinen and Savijrvi2011; Schalkwijk and others, Reference Schalkwijk, Jonker and Siebesma2013), particularly those in which large-scale effects are disregarded (Darbieu and others, Reference Darbieu2015) and when the impact of small-scale heterogeneities is analyzed in the context of larger-scale averages over short periods of time (Zhu and others, Reference Zhu, Ni, Cong, Sun and Li2016). Nevertheless, the simulations initialized with strong wind have to be treated with caution, since in the real atmosphere, high winds are always associated with high larger-scale pressure gradients not prescribed in the present study.
The model domain parameters are set on the basis of WRF model guidelines (Wang and others, Reference Wang2017) and other modeling studies of convective motions in the ABL. Several analyses of convective ABLs, similar to the present one in terms of the vertical and horizontal scales, have been performed for the lower latitudes (e.g. Wang and Feingold, Reference Wang and Feingold2009a, Reference Wang and Feingoldb; Yamaguchi and Feingold, Reference Yamaguchi and Feingold2015) with a LES approach and grid spacing ranging from 100 m to 500 m. Analogous model frameworks have also been used in studies of the atmospheric dynamics over complex terrain (e.g. Rotach and Zardi, Reference Rotach and Zardi2007; Lundquist and others, Reference Lundquist, Chow, Lundquist and Mirocha2008). Zulauf and Krueger (Reference Zulauf and Krueger2003a) examined the development of convective plumes with a horizontal resolution of 200 m and obtained results corresponding to the observational data. The suitability of WRF ARW for LES simulations for convective boundary layers has been analyzed in detail by Moeng and others (Reference Moeng, Dudhia, Klemp and Sullivan2007) who concluded that the results are statistically comparable with observations, laboratory data and other modeling studies. Therefore, we regard the model setup presented below as reasonable and applicable to the performed analysis, although, obviously, the model resolution sets a limit on the smallest sea ice features and associated atmospheric response that can be resolved.
In our simulations, the model domain is rectangular, with periodic boundaries in both horizontal directions, dimensions 200 × 200 and horizontal resolution of 100 m, thus covering the area of 20 000 m × 20 000 m. The top model boundary is set at 2000 m above the surface, close to the top of the inversion layer separating the ABL from the free atmosphere in the initial sounding (Fig. 2). Initial model tests have shown that this is well above the height reached by the strongest convective updrafts (1100–1200 m). At the upper model boundary, a damping zone is defined as a Rayleigh relaxation layer of 200 m depth, with a default damping coefficient of 0.003 s−1. The vertical velocity component at the top of the model domain is set to zero. Air column is divided into 61 vertical levels with exponential thickness distribution, from ~2 m at the surface to ~200 m at the top. Each simulation described below was performed for 14 hours, with a time step of 1 s. The results were stored every 10 minutes.
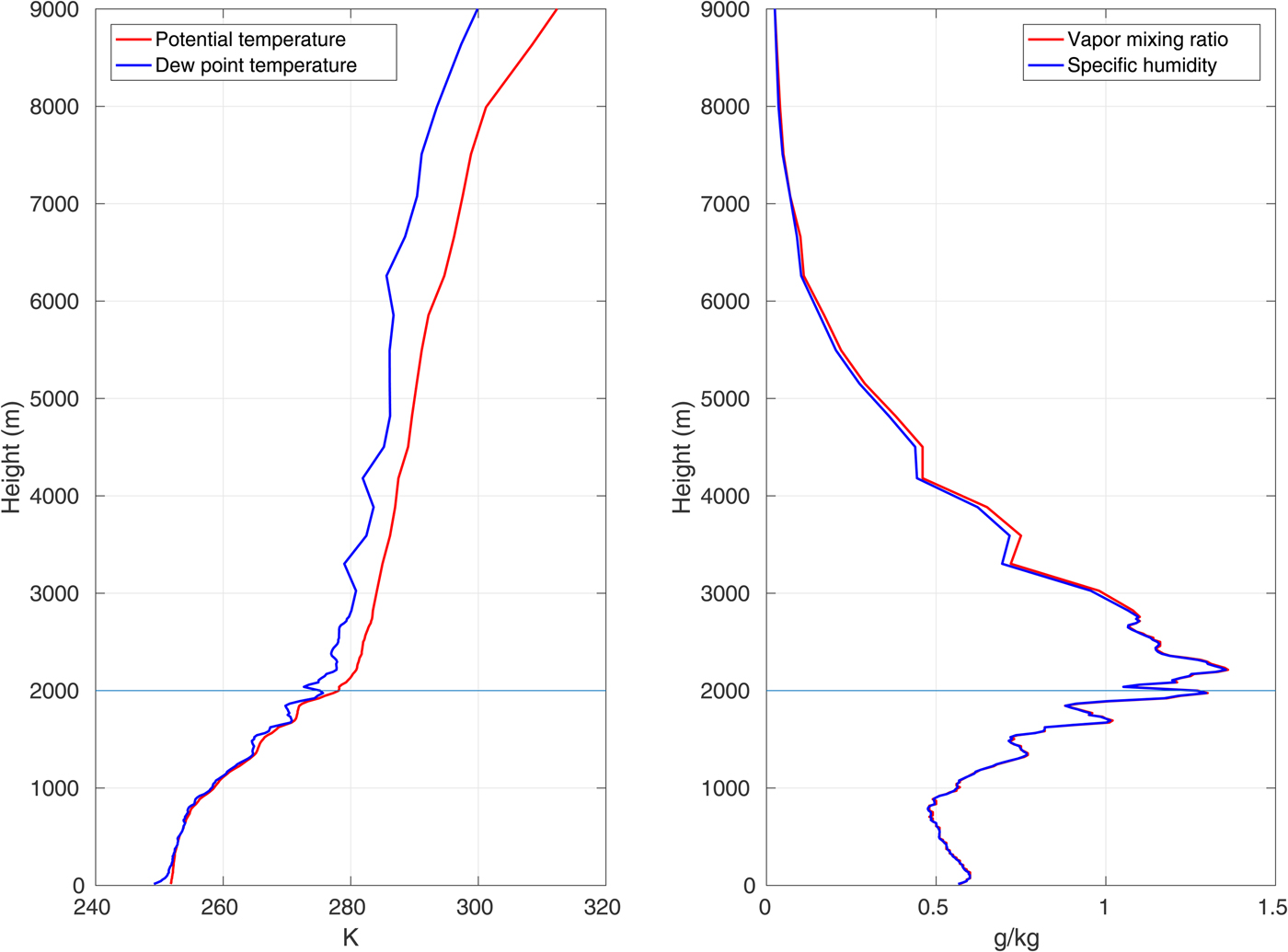
Fig. 2. Potential temperature and water vapor mixing ratio profiles used in simulations with calculated profiles of dew point temperature and specific humidity. Lines at the height of 2000 m indicate the top boundary of the model.
Parametrization schemes of physical processes are chosen on the basis of the WRF model validation performed in other studies under similar conditions. The Single-moment 5-class scheme, Eta Similarity Scheme (based on the Monin–Obukhov similarity theory with Zilintkevich thermal roughness length and standard similarity functions; Monin and Obukhov, Reference Monin and Obukhov1954; Janjic, Reference Janjic2002; Hong and others, Reference Hong, Dudhia and Chen2004), along with the NOAH land surface model (Tewari and others, Reference Tewari2004) have been tested and found optimal for the Arctic by Bromwich and others (Reference Bromwich, Hines and Bai2009). WRF Single-moment 5-class Scheme introduces five categories of moisture: water vapor, cloud water, cloud ice, rain water and snow. Contrary to older schemes, it allows supercooled liquid water to exist (Hong and others, Reference Hong, Dudhia and Chen2004). In another evaluation of Polar WRF (Wilson and others, Reference Wilson, Bromwich and Hines2012), the RRTMG (Rapid Radiative Transfer Model for General Circulation Models) scheme (Iacono and others, Reference Iacono2008) is recommended for usage in the polar regions for both longwave and shortwave radiation processes, although obviously the latter is not relevant in polar winter conditions considered here. Due to the high horizontal resolution of the present analysis, the cumulus and boundary layer schemes could be disregarded (Wang and others, Reference Wang2017). Therefore, the physical processes in the ABL are determined by turbulence closure and diffusion schemes, with activated vertical diffusion routines – as in the WRF LES mode.
Diffusion options included in the WRF model are selected to accurately simulate the processes at the horizontal resolution of 100 m. Following the suggestions in the WRF users guide (Wang and others, Reference Wang2017) and the technical description of the model (Skamarock and others, Reference Skamarock2008), the recently developed 3rd-order Runge-Kutta time integration scheme have been selected for the simulations. Based on a similar approach, a positive-definite scheme for the advection of moisture is used to guarantee the proper performance of the model.
We tested two different turbulence schemes available for idealized simulations in WRF: Smagorinsky first-order closure, and 1.5-order TKE (turbulent kinetic energy) prediction scheme. Several selected simulations were launched twice, with identical conditions, but different turbulence closures. Both methods can represent horizontal and vertical subgrid-scale mixing in the boundary layer and the free troposphere. However, the tests showed that the first one tends to produce instabilities in the results and unrealistically high values of horizontal and vertical wind components. What is more, the 1.5-order TKE prediction scheme allows it to explicitly predict the intensity of turbulent kinetic energy along with additional parameterization of potential temperature variance (Stensrud, Reference Stensrud2007). Therefore, results obtained with the 1.5-order TKE scheme are used for the analysis presented in this paper. Additionally, with the Planetary Boundary Layer scheme turned off and full diffusion turned on in the WRF model, the selected scheme is the one recommended for the analysis of ABL with grid spacing lower than ~2 km (Moeng and others, Reference Moeng, Dudhia, Klemp and Sullivan2007; Wang and others, Reference Wang2017). The 1.5-order turbulence scheme is also the one usually applied to WRF model simulations with similar model parameters (Antonelli and Rotunno, Reference Antonelli and Rotunno2007; Moeng and others, Reference Moeng, Dudhia, Klemp and Sullivan2007; Rotunno and others, Reference Rotunno2009; Lundquist and others, Reference Lundquist, Chow and Lundquist2010; Crosman and Horel, Reference Crosman and Horel2012). The results obtained in the aforementioned studies are comparable with the observational data, further supporting our choice of this turbulence scheme.
The fractional sea-ice option introduced to WRF by Bromwich and others (Reference Bromwich, Hines and Bai2009) and tested in various studies (e.g. Bromwich and others, Reference Bromwich, Hines and Bai2009; Hines and others, Reference Hines2015) is also used in our simulations. Other sea-ice parameters are set as default values in the model, apart from the sea-ice thickness which is set to 1.5 m, a typical value for Arctic winter sea ice (Perovich. and others, Reference Perovich2003). A full list of parameters describing the model setting can be found in Supplementary Table 1.
Each simulation with the WRF model was launched with identical vapor mixing ratio and potential temperature profile. The initial conditions in each case were horizontally homogeneous over the whole model domain, i.e. exactly the same over the ice-covered and the ice-free grid cells. Consequently, the presence of surface instability sources, like open water, significantly affected the ABL structure and resulted in rapid heat and moisture release to the atmosphere, producing strongly enhanced values of quantities such as the cloud liquid water (Q c,tot) or turbulent fluxes in the first simulation hour (Supplementary Figs 13a and 14) as the time needed to reach a quasi-stationary state under the applied forcing. We decided to display the values of the whole simulations in the time series plots, but the first hour is not taken into account in the analysis.
Initial conditions
The model box is placed at 75°N, 160°W, i.e. at the location of the SHEBA experiment (Uttal and others, Reference Uttal2002). The Coriolis force, corresponding to this latitude, is assumed constant and the Coriolis parameter is equal to 1.417 × 10−4 s−1. As has been described in the previous section, the initial atmospheric conditions are horizontally uniform and are provided as vertical profiles of temperature, water vapor mixing ratio and of wind velocity. In order to obtain conditions typical for an Arctic winter, the necessary variables are acquired from the SHEBA dataset, based on measurements collected by a meteorological balloon, with a rawinsonde for wind measurements attached to it. We decided to use observations from 23 February 1998, 11.15 a.m. (Uttal and others, Reference Uttal2002). It is worth mentioning that the ice concentration around SHEBA on 23 February 1998 equaled ~99% and it remained higher than 96% within an area of a radius of a few tens of kilometers around the station (based on 10-km gridded OSI SAF ice concentration data). The results of other measurements performed at the SHEBA location show that the ABL on that day was clouded up to the height of 1500–2000 m, with liquid water path of ~120 g × m−2 driving surface mixing to ~600 m through longwave radiation (Shupe and Uttal, Reference Shupe and Uttal2007; Uttal, Reference Uttal2007; NCAR/EOL, 2014) (Supplementary Note S1). Therefore, the selected profile represents a rather deep surface-mixed-layer, which although not prevalent, is regularly observed in the Arctic MIZ (Esau and Sorokina, Reference Esau, Sorokina, Langand and Lombarg2010). The results of the ECMWF model from that location show that the vertical air velocity within ABL was very low, below ±0.05 Pa s−1, with slightly higher values in the layers above the ABL. Notably, values as high as ±0.5 Pa s−1 were observed over the SHEBA location on other days (Andreas and others, Reference Andreas, Fairall and Persson2007). This is another argument for using this particular profile in our simulations – we can be certain that the high vertical velocities obtained can be attributed to local, small-scale effects over leads and spaces between ice floes rather than to the regional instability of the atmosphere. It is also worth pointing out that it is difficult to define average/representative conditions over fragmented sea ice, as the vertical profiles measured at different locations within a relatively small area may be very different. This is exactly the main message of this work. In other words, if we were able to find horizontally uniform initial conditions for our model perfectly representing the state of the ABL, it would be a serious argument against the conclusions of our study.
The method of calculating the WRF input from the measurement data is described in Supplementary Note S1 and the resulting profiles are shown in Fig. 2. We assume for simplicity that at the start of each simulation the wind blows from west to east. For each sea-ice mask (see below), the simulations are run 6 times: with wind speed equal zero at the beginning of the model run, and for five different wind speed profiles obtained by modifying the measured values, as shown in Fig. 3. The second wind profile is the one acquired from the SHEBA dataset (Uttal and others, Reference Uttal2002). The first and third profiles were obtained by multiplying the original one by 1/2 and 2, respectively. In the fourth and fifth wind profiles, we prescribed the surface wind speed as, respectively, 5 and 7.5 times higher than the measured one and calculated its height-variability by adding the same gradient between each layer as in the original profile. Note that only levels below 2000 m are relevant for our study. Note also that, whereas the wind profiles varied in different simulations, other initial parameters remained the same, so that the conditions associated with the fourth and fifth wind profiles are rather unrealistic and should be treated with caution; their purpose is to estimate the model sensitivity to a wide range of conditions. Considering the lower ~1000 m of the ABL, within which the convective motion takes place, the vertically averaged values of wind speed from the profiles are as follows: 1.06 m s−1 for 1st wind profile, 2.1 m s−1 for 2nd one, 4.26 m s−1 for 3rd one, 7.4 m s−1 for 4th one and 9.35 m s−1 for 5th one. An example evolution of the ABL in time is presented in the Supplementary Figs 11 and 12 for the simulation with prescribed zero wind speed, sea-ice concentration 50% and 20 leads.
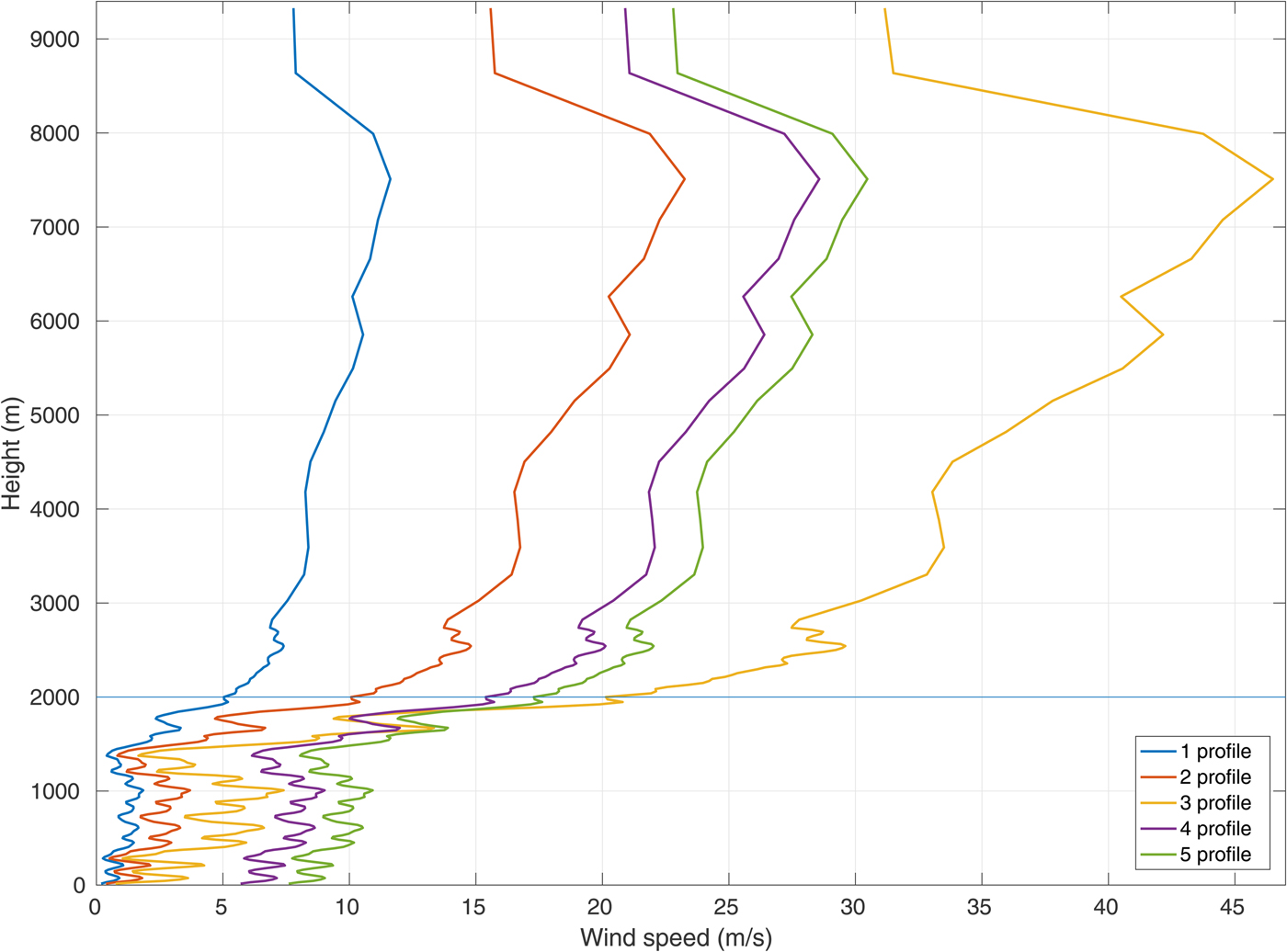
Fig. 3. Wind profiles used in model simulations. Line at the height of 2000 m indicates the top boundary of the model.
The freezing point of sea water is set to T f = 271.4 K and the surface water temperature is set to T f. The initial temperature within sea ice varies linearly from T f at the bottom to the air temperature at the upper ice surface. The default values of the roughness length z 0 are used, i.e. z 0 = 1.0 × 10−4 m over water and z 0 = 1.0 × 10−3 m over the ice. The observed values of the sea-ice surface roughness over a multi-year floe during the SHEBA campaign varied throughout the year between 3 and 11 × 10−4 m (Persson and others, Reference Persson, Fairall, Andreas, Guest and Perovich2002). For winter conditions at the SHEBA location, the value of 2.3 × 10−4 has been suggested by Andreas and others (Reference Andreas2010). Thus, the default WRF value of z 0 over sea ice represents the higher end of the observed variability range. To test the model sensitivity to this parameter, we performed additional model runs with the value of z 0 = 2.3 × 10−4 m. The results obtained did not differ significantly from the default ones. Maximum surface wind speed increased by 0.8 m s−1 and area-averaged values of latent and sensible heat flux were almost identical. The maximum difference between domain-averaged liquid water content was 0.5 × 10−4 kg m−2 (and much lower during most of the simulation), while the variations of water vapor content were insignificant. Furthermore, the overall structure and strength of convection also remained very similar. Considering these results and the fact that the default value of z 0 lies within the range of the observed ones, it is used in all model simulations.
Sea-ice masks
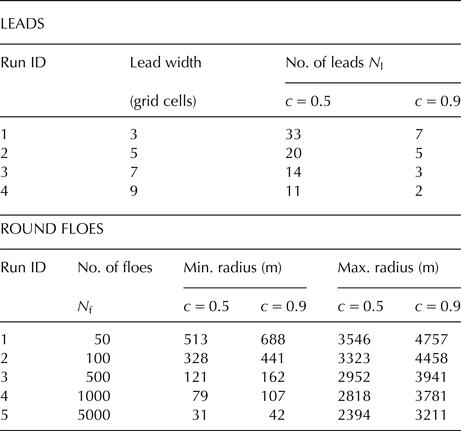
In the present study, two different sea-ice concentration values are considered: c = 50% and c = 90%. The WRF model was also launched for other ice concentrations as well (60, 70 and c = 80%), but we decided to focus on the ones presenting the most contrasting results (c = 50% and c = 90%). For each ice concentration and wind speed profile, the model is launched for a series of simulations with the different spatial distribution of ice, including: (i) a various number of equally-spaced leads with specified widths and (ii) round floes with a power-law size distribution (Fig. 4, Supplementary Figs 2–10). In the case of leads, the distribution of sea ice in our simulations is based on binary ice masks, where each grid cell is either open water or thick ice. The width of leads varies from 200 m (an ice map with N l = 33 for c = 50%) to 1000 m (an ice map with N l = 2 for c = 90%). In the case of round floes, a power-law probability distribution P(r) of their radii is assumed, P(r) ~ r −α, with an exponent α = 1.8 (values between 1.5 and 2.0 are typically observed in the MIZ; see e.g. Toyota and others, Reference Toyota, Takatsuji and Nakayama2006; Herman, Reference Herman2010, and references there). Floe radii range from several tens of meters to over 4 km. The sea-ice masks for WRF are obtained by first generating an ensemble of floes with a desired total ice surface area, corresponding to a prescribed c and number of floes N; subsequently, these floes are randomly placed within a temporary, very large rectangular domain at a very low ice concentration and without floe overlap and a discrete-element (DEM) model (Herman, Reference Herman2016) is used to reduce the size of that domain and to obtain the final floe positions, from which eventually an ice concentration map is computed. In other words, the DEM is used to converge the initially loosely packed floe assemblage to obtained a desired ice concentration – which is otherwise a rather nontrivial task. A summary of all lead and floe configurations considered is given in Table 1. Corresponding sea-ice maps are shown in Supplementary Figs 2–10.
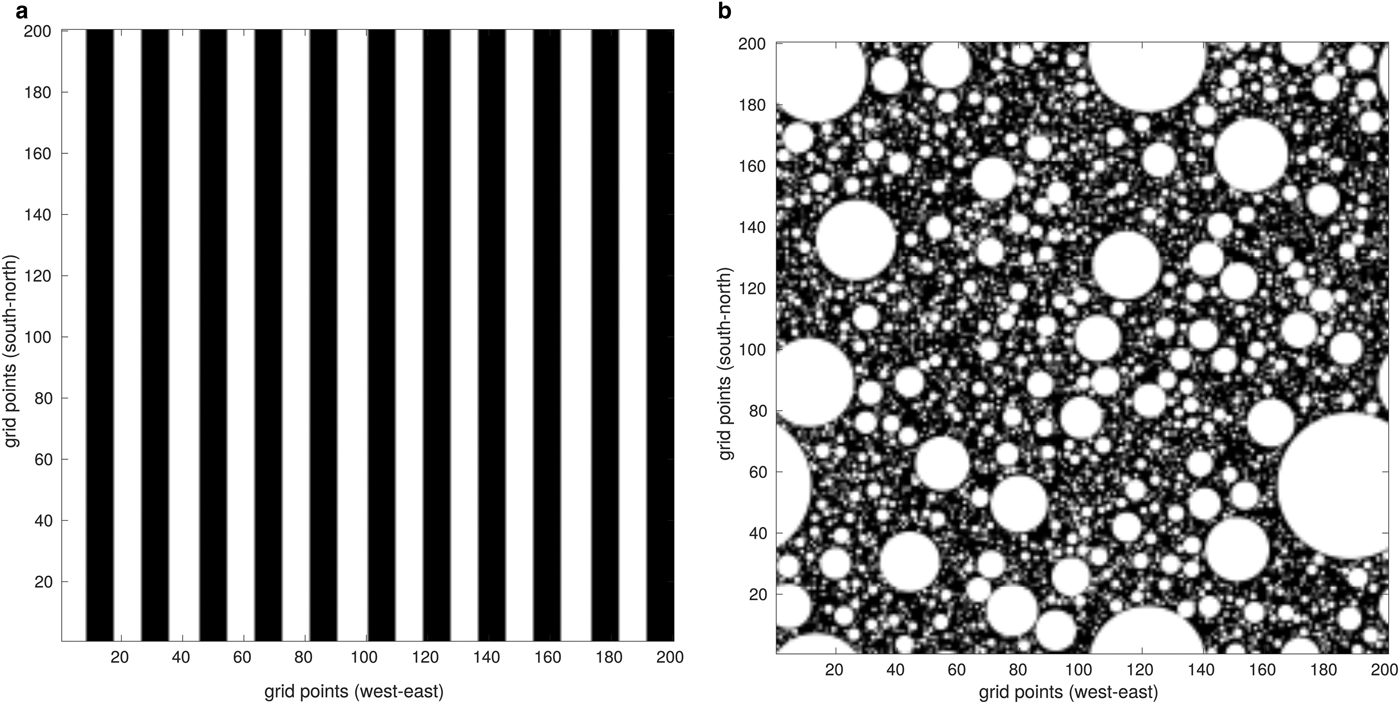
Fig. 4. Sea ice maps for ice concentration c = 50%, (a): number of leads N l = 11, (b): number of floes N f = 5000. See Supplementary Figs 2–10 for the remaining sea ice maps.
Table 1. Properties of leads and floes used in the simulations.
RESULTS
In this section, we analyze the structure of the ABL circulation, as well as selected domain-averaged variables characterizing the ABL and the sea ice/atmosphere interactions: the domain-averaged total (i.e. vertically integrated from the surface to the top boundary of the model) water vapor and liquid water content further denoted with Q v,tot and Q c,tot, respectively, and expressed in kg m−2; and domain-averaged surface latent and sensible heat flux, denoted with F l and F s, respectively, and expressed in W m−2. For these variables, we analyze the sensitivity to different wind profiles and sea-ice configurations.
The role of ambient wind speed and direction
Throughout the time of each simulation, local wind direction varies periodically due to inertial oscillations. Their presence is a consequence of using periodic lateral boundary conditions, which effectively decouple the model domain from any outside forcing so that the wind direction changes in time due to the Coriolis force. The period of those oscillations corresponds exactly to the inertial period at the latitude of our simulation box. (~ 12.3 h).
Furthermore, thermal and dynamical instabilities of air flow over sea ice/open water areas initiate convective motions over the modeled area. Due to the heating from the water along with variations of wind shear over different types of surface, the upward motion of air is generated. In the simulations with zero ambient wind speed or weak wind conditions (profile No. 1, Fig. 3), several divergence and convergence zones can be observed (Fig. 5). The areas, where the flow from different directions attains the highest speed, are associated with convergence and upward air motion, whereas locations of surface divergence are associated with no or very weak vertical motions in the downdraft direction. The spatial arrangement and size of the convective structures (divergence and convergence zones) differ in cases with leads and floes (Fig. 5). When leads are present, convective structures tend to develop between each strip of open water, while in configurations with floes they are organized around the largest floes. When the ambient wind is stronger (profiles No. 2–5 in Fig. 3), divergence–convergence areas do not develop (Fig. 6). However, here again, areas of increased horizontal wind speed are associated with upward air motion and, accordingly, weak local wind conditions with slow downward air flow. The maximum speed of the vertical wind component varies from ~0.5 m s−1 (profiles No. 1, 2 and zero-wind conditions) to ~3 m s−1 (profiles No. 3–5) in the centers of convective plumes. The extreme values are short-lived and occur only at single pixels of the model, average updraft speeds are significantly lower and vary between 0.03−0.05 m s−1. As already mentioned, the convergence of the horizontal wind vectors and the vertical air motion associated with it tend to occur in the same areas throughout the time of the simulation, as they are directly related to the location of ice floes.
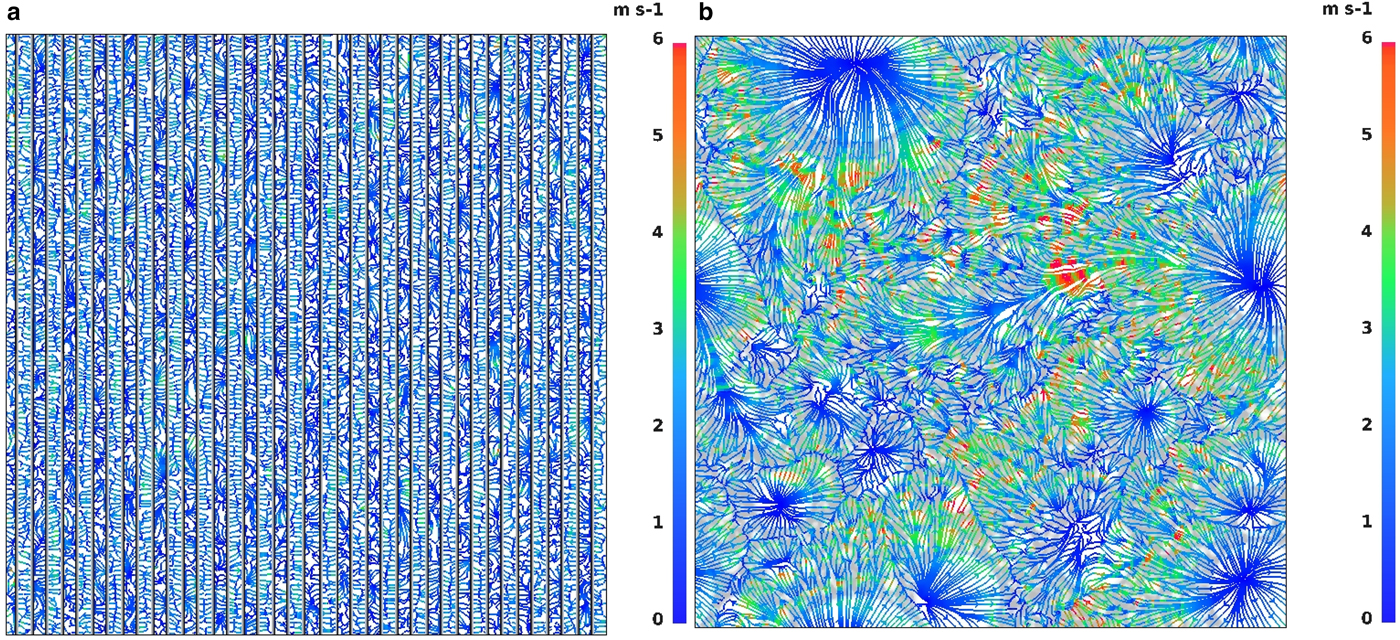
Fig. 5. Surface streamlines with wind speed (m s−1) for ice concentration c = 50%; (a): zero initial wind, N l = 20, (b): wind profile No. 1 (Fig. 4), N f = 5000.
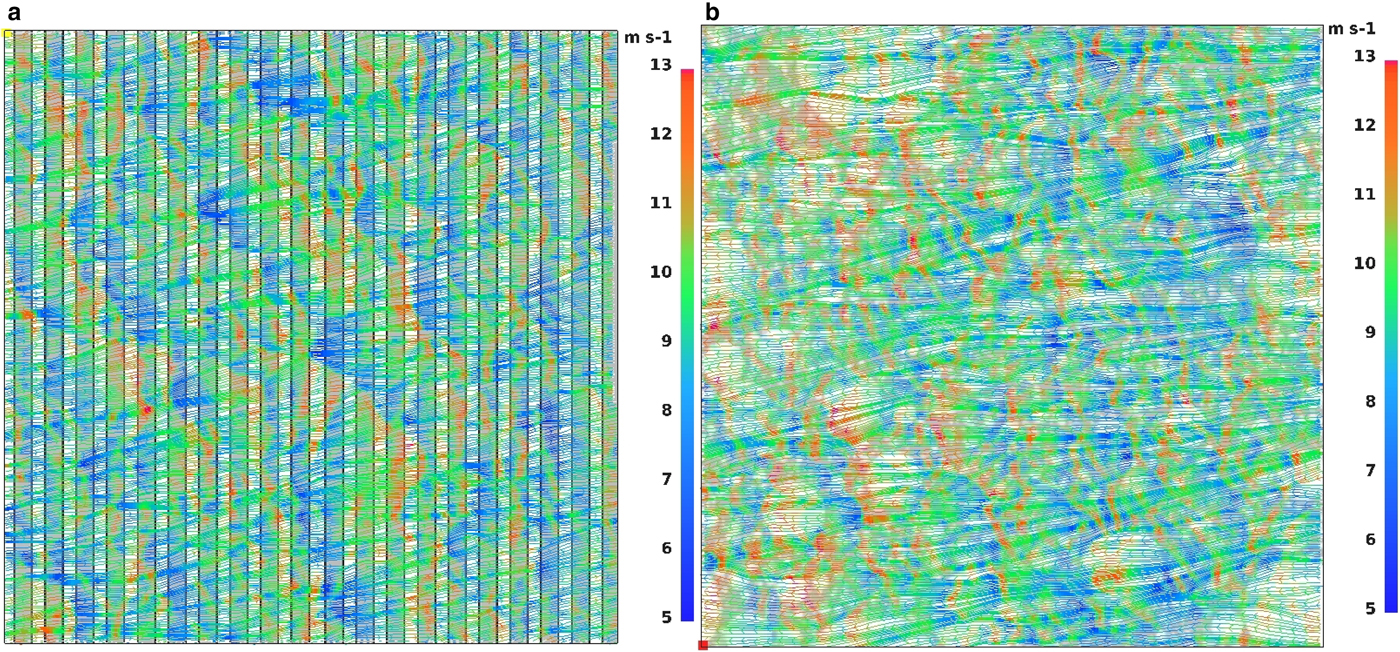
Fig. 6. Surface streamlines with wind speed (m s−1) for initial wind profile No. 5 (Fig. 4) and ice concentration c = 50%; (a): N l = 20, (b): N f = 5000.
As mentioned above, higher ambient wind speeds suppress the development of regular convective structures. Stronger wind enforces enhanced mixing of moist air formed above the open water with adjacent air masses. Therefore, in situations with higher wind speeds, higher values of moisture content are observed over the ice-covered areas. In agreement with other studies of the lead impact on the ABL (Alam and Curry, Reference Alam and Curry1997; Burk and others, Reference Burk, Fett and Englebretson1997; Andreas and Cash, Reference Andreas and Cash1999), those situations tend to occur downwind of sea-ice fractures, as stronger wind enhances the mixing of air above the water surface and intensifies the heat transport. This effect is most recognizable in cases with two leads present in the model domain (Fig. 7). Analysis of horizontal air flow maps reveals also that in simulations with the strongest ambient wind (profiles No. 4, 5), the low-level wind speed maximum is located not directly over open water, but downwind of leads (Fig. 7a). When the area-averaged wind speed is low, the local wind tends to be stronger over water than over ice due to differences in surface roughness z 0 (see Fig. 5a), as observed, for example by Tetzlaff and others (Reference Tetzlaff, Lümlpkes and Hartmann2015). However, very strong advection associated with wind profiles 4 and 5 apparently dominates over effects related to surface roughness, so that both the surface wind speed maximum (Fig. 7a) and the strongest updrafts (not shown) are shifted in the downwind direction.
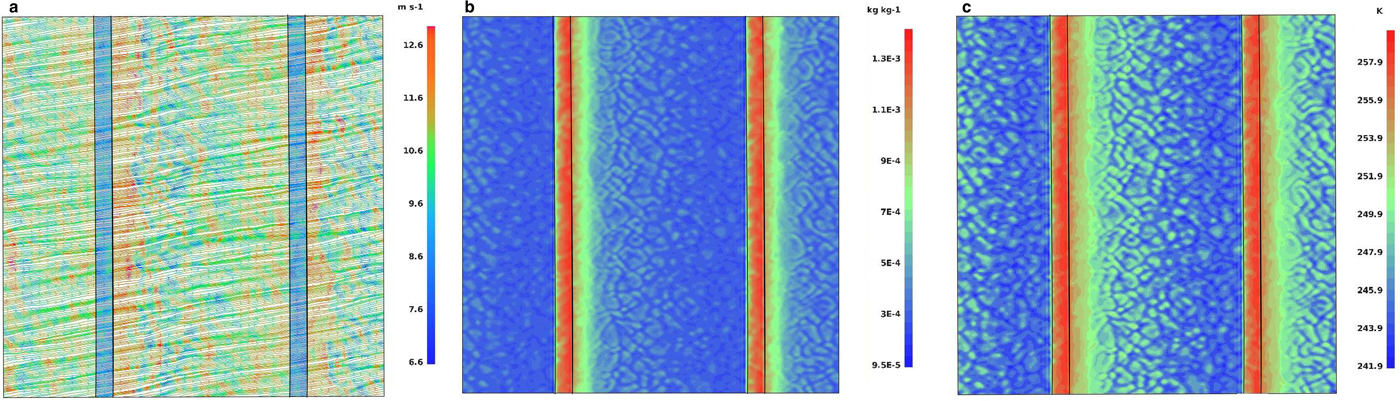
Fig. 7. Results of simulation with wind profile No. 4 (Fig. 4), ice concentration c = 90%, N l = 2; (a): surface streamlines with wind speed (m/s), (b): water vapor mixing ratio (kg kg−1) 2 m above the surface, (c): air temperature (K) 2 m above the surface.
Other consequences of a strong ambient wind speed are also similar to those found in several previous analyses of turbulent fluxes and ABL characteristics (Alam and Curry, Reference Alam and Curry1995; Burk and others, Reference Burk, Fett and Englebretson1997; Lümlpkes and others, Reference Lümlpkes2008a). We observe increased values of F l, F s, as well as Q v,tot and Q c,tot with increasing wind speeds (Supplementary Figs 13 and 14). This dependence appears to be more powerful for stronger wind speeds; the results for the first three wind profiles are repeatedly close to each other and differ from the remaining two (Supplementary Fig. 13a). Moreover, the analysis of the domain-averaged turbulent fluxes reveals that stronger wind produces higher temporal variability of the atmospheric circulation (Supplementary Figs 13a and 14a).
The role of ice concentration
Several differences between the results for the two sea-ice concentrations examined (c = 50% and c = 90%) have already been mentioned. As might be expected, the variations are quite significant as ice concentration is one of the dominating factors determining sea ice/atmosphere interactions (e.g. Lümlpkes and others, Reference Lümlpkes, Vihma, Birnbaum and Wacker2008b; Seo and Yang, Reference Seo and Yang2013).
As a consequence of large sea surface/air temperature difference, the highest water vapor and cloud liquid water content along with positive values of turbulent fluxes are observed over open water (Fig. 8a) in contrast to the areas covered by sea ice. These results correspond well with the analysis of Glendening and Burk (Reference Glendening and Burk1992); Burk and others (Reference Burk, Fett and Englebretson1997); Overland and others (Reference Overland2000), who also mentioned negative downward fluxes above the ice balancing the updraft generated over open water. The same pattern can be observed in our results (Fig. 8b). Moreover, comparison of the time variability of Q v,tot for c = 50% and c = 90% reveals substantial differences in the results. Although, as already mentioned, we observe high Q v,tot during the first hour (spin-up) of the simulations, it increases noticeably with time in cases with c = 50% and decreases for c = 90%. Additionally, the values of Q v,tot are not very sensitive to details of the spatial sea-ice distribution with identical ice concentrations (Supplementary Fig. 15).
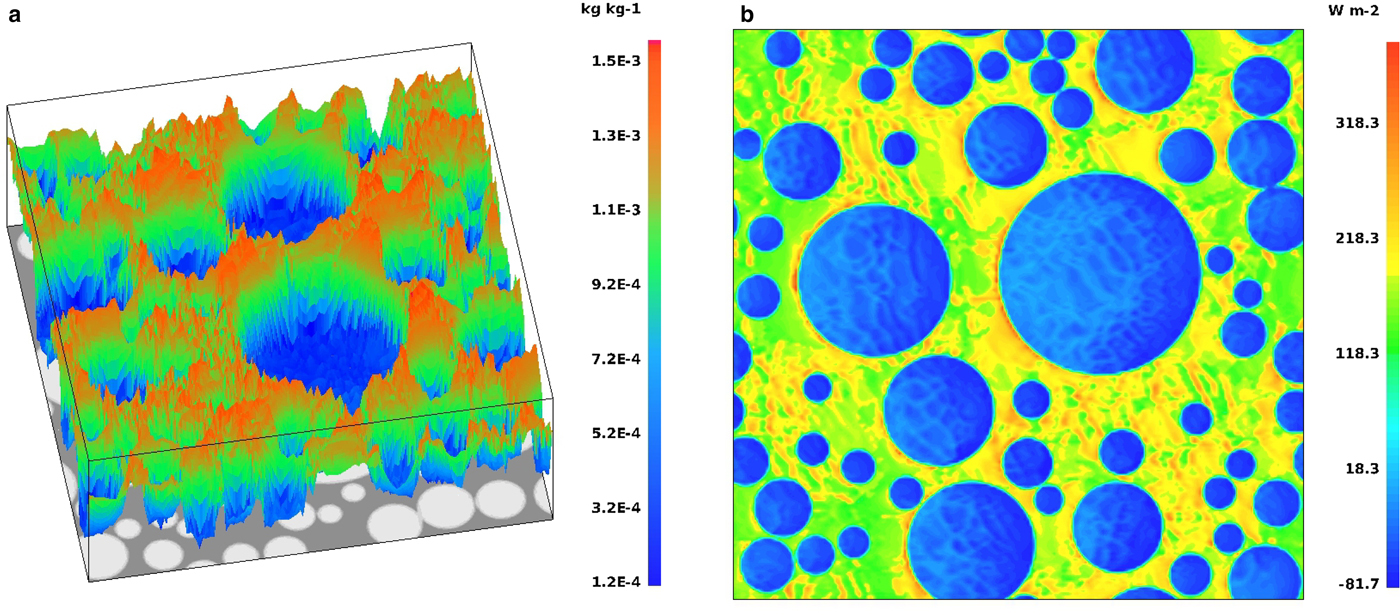
Fig. 8. Results for wind profile No. 3 (Fig. 4), ice concentration c = 50%, number of floes N f = 50, (a): water vapor mixing ratio (kg kg−1), (b): surface sensible heat flux (W m−2).
As we analyze more closely the results for identical ice concentrations, but different N f and N l, there are a few more things to point out. Comparison of the values of turbulent fluxes along with water vapor and liquid water content reveal comparable variations for different ice distributions with both ice concentrations, c = 90% and c = 50% (Fig. 9; note different vertical scales in the two panels). At both ice concentrations, the F l variability equals 20% of its mean values of 5–6 W m−2 and 25–30 W m−2, respectively, indicating limited sensitivity to different distributions of floes and leads. On the whole, the values of the analyzed quantities are significantly larger at c = 50%. Similarly to other described cases, they are also notably dependent on the ambient wind speeds, which intensifies the atmospheric response.
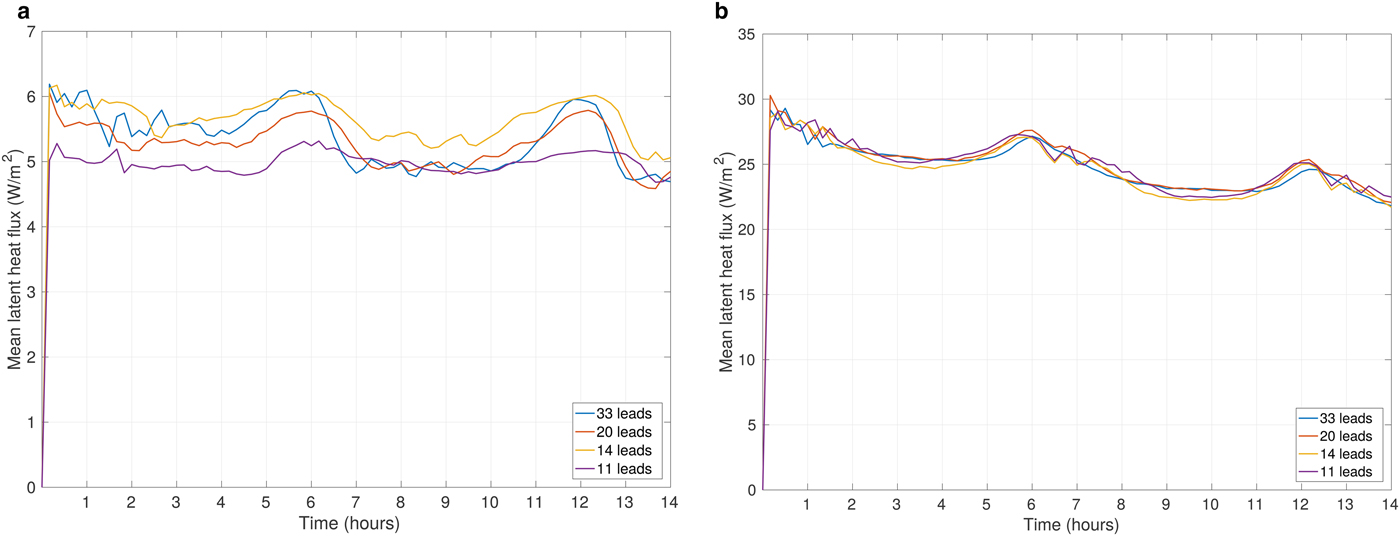
Fig. 9. Area-averaged latent heat flux (W m−2) for wind profile No. 2 (Fig. 4) and different N l, (a): ice concentration c = 90%, (b): ice concentration c = 50%.
In this paper, we primarily concentrate on the influence of the spatial ice distribution on the ABL, which is more pronounced in the simulations with an ice concentration of c = 90%. Therefore, we mostly focus on those in the further analysis; simulations with c = 50% are discussed only in the cases in which their results differ significantly from those for c = 90%.
Effect of leads/floes configuration on the moisture content in the ABL
Water vapor originating from open-water areas condenses into small liquid water droplets of several micrometers width, which enables their persistence at Arctic wintertime temperatures (Andreas and others, Reference Andreas, Miles, Barry and Schnell1990). As already mentioned, in our modeling results the highest values of Q c,tot are obtained at the beginning of each simulation, during the aforementioned spin–up phase of the simulations. Apart from this feature, the results vary substantially for different sea-ice concentrations and spatial distributions.
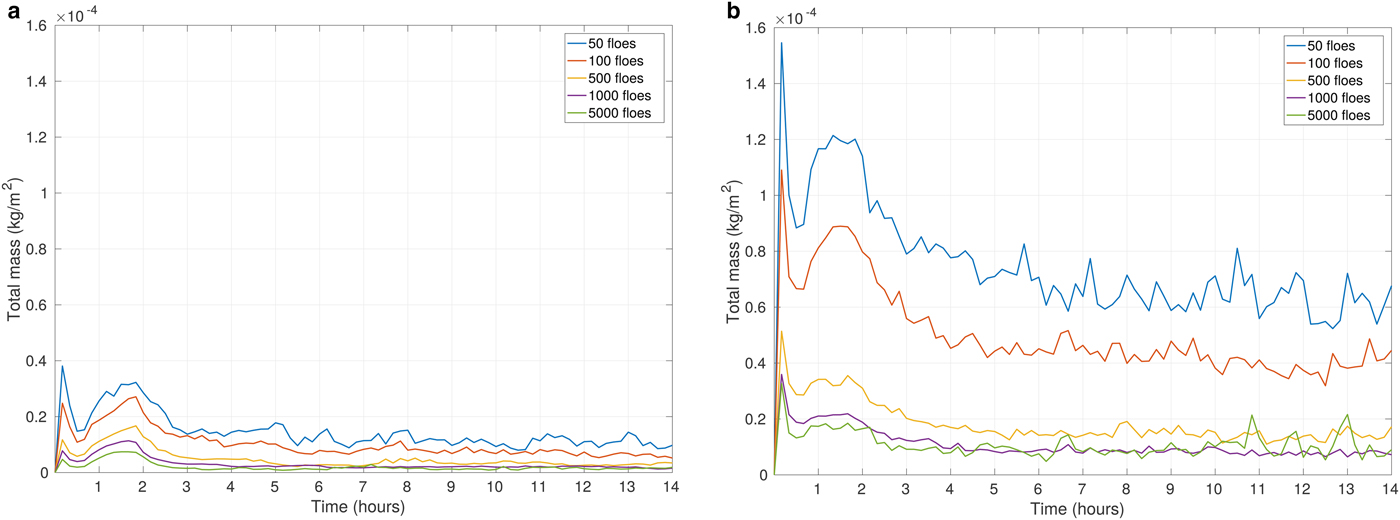
The values Q c,tot are analyzed for the ice concentration of 90% and for a various number of leads. Unsurprisingly, increasing wind speed generally enlarges Q c,tot in the ABL. However, the smallest values are not associated with simulations initialized with zero ambient wind at the beginning of model run (Fig. 13a), but with the weak-wind conditions of profiles No. 1 and 2. The reason for this apparent paradox is that mild average wind reduces local wind velocities associated with convective motions, thus reducing the amount of moisture released from the water surface. This result shows that the area-averaged response of the atmosphere to the underlying sea-ice structure is far from linear, as local circulations interact with larger-scale air flow. It is also worth noticing that, apart from the peak of Q c,tot at the beginning of the simulation, its value remains rather stable in time in situations without ambient wind.
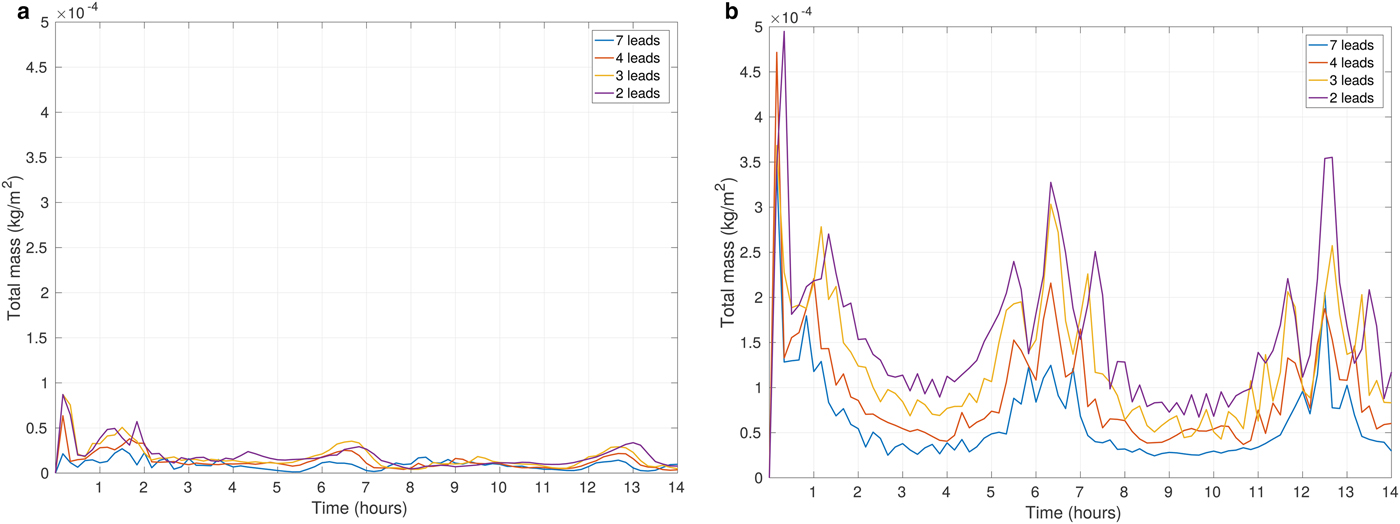
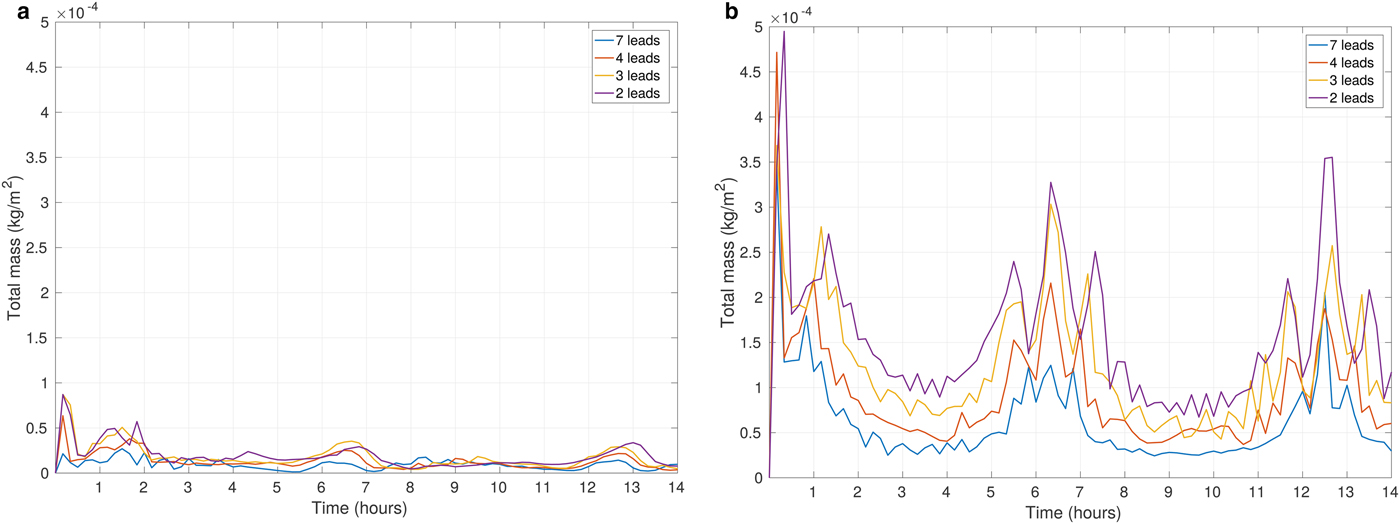
Due to the aforementioned inertial oscillations, the overall wind direction periodically becomes parallel or perpendicular to the direction of the leads. Consequently, we observe an associated periodic intensification of heat and moisture release from the surface every time when the wind blows in the along-lead direction. Due to a long fetch, the wind over a lead accelerates, reinforces the release of heat and moisture from the open water, and consequently leads to the larger values of Q c,tot in the atmosphere (Fig. 10). Naturally, when the ambient wind speed increases, the periodic peaks in the values of the analyzed quantities are even more distinctive (Fig. 10b). We presume that higher moistening of the ABL for fewer leads (Fig. 10b) is a consequence of a slightly (~1 K and lower) warmer surface layer in simulations with two leads in comparison with those with larger numbers of leads. Significant amounts of moisture present in the ABL make the model very sensitive to even slight differences in the ambient conditions. Nonetheless, those results have to be analyzed with some caution, as they are related to the artificially modified conditions linked with strong wind profiles, as mentioned in the section Initial Conditions.
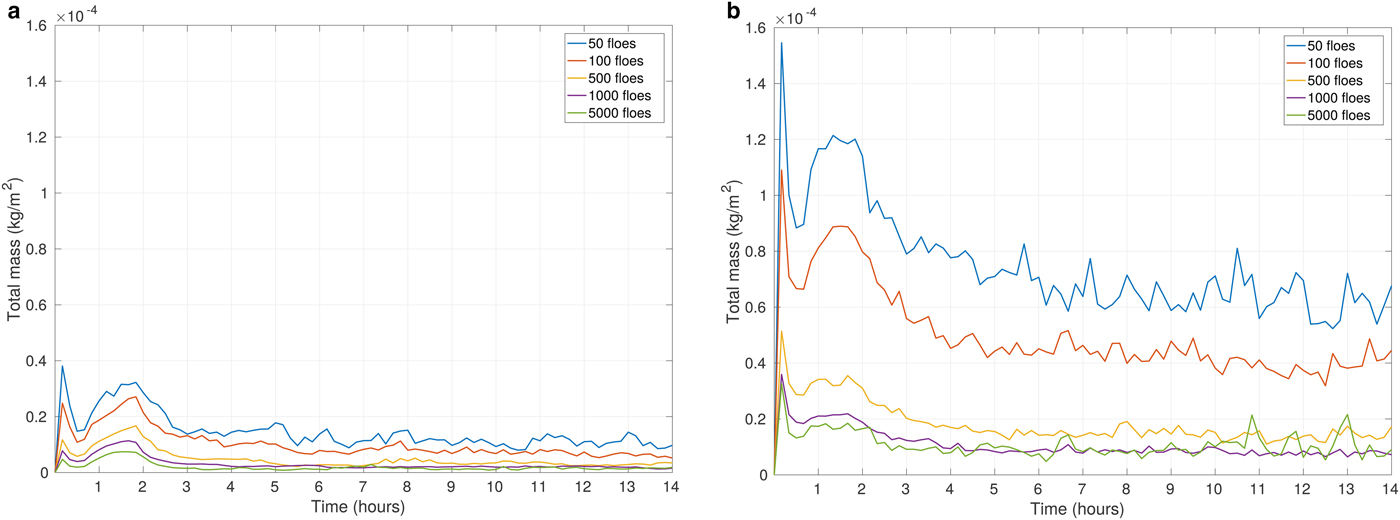
When the simulations with round floes with various N f are considered, the situation is slightly different. Similar to the case with leads, the increase of ambient wind speed substantially increases the total moisture content in the ABL (Fig. 11). Q c,tot reaches its maximum just after the end of model spin-up time and decreases rapidly within the next hour. After approximately 3 hours the values of Q c,tot reach a stable level with small fluctuations, or slight decrease for the rest of the simulation period (Fig. 11). The inertial oscillations do not affect those simulations in any noticeable way, as the spaces between ice floes are randomly oriented and cannot directly align with the wind direction.
In simulations with round floes, the number of floes N f determines the fragmentation of open water areas between the floes. Regardless of the fact that ice concentration remains constant for various floes arrangements, the value of Q c,tot varies between the simulations. The highest Q c,tot is associated with cases of N f = 50 and N f = 100 (Fig. 11). In other words, the size of the individual open water ‘patches’ is an important factor shaping the ABL response and influencing the total moisture content – up to a certain threshold size. The minimum Q c,tot might be expected to emerge in simulations with N f = 5000 of densely packed floes. However, the results are slightly different. In our analysis, the smallest amount of Q c,tot is associated with the case of N f = 1000, although the relationship is not very consistent as the results for ice maps with N f = 500, N f = 1000 and N f = 5000 do not differ much from each other. We may conclude that the most significant differences occur between the model results with the large ice floes (N f = 100 and N f = 50) and those with smaller ice floes (N f = 500, N f = 1000 and N f = 5000; see Fig. 11).
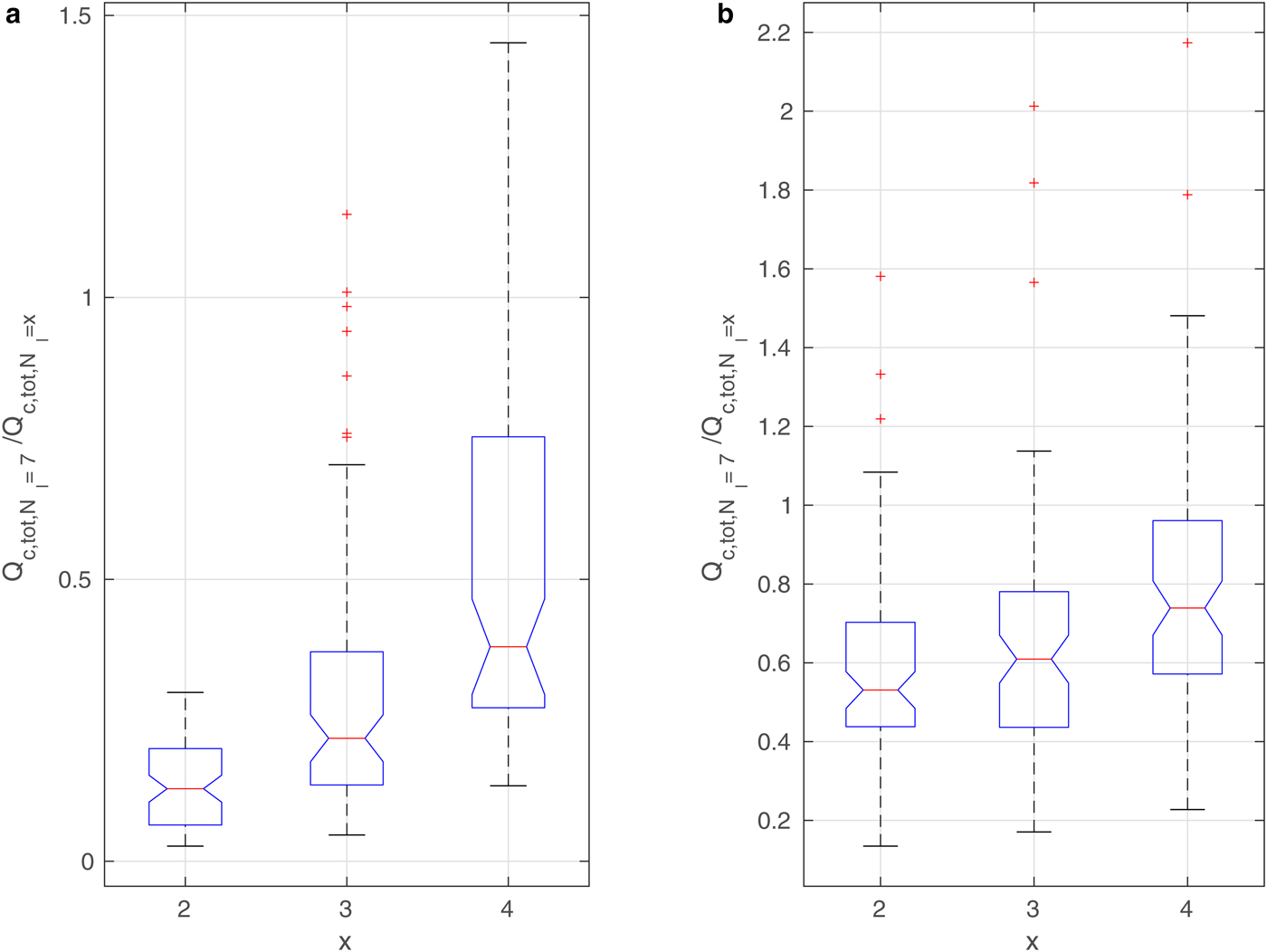
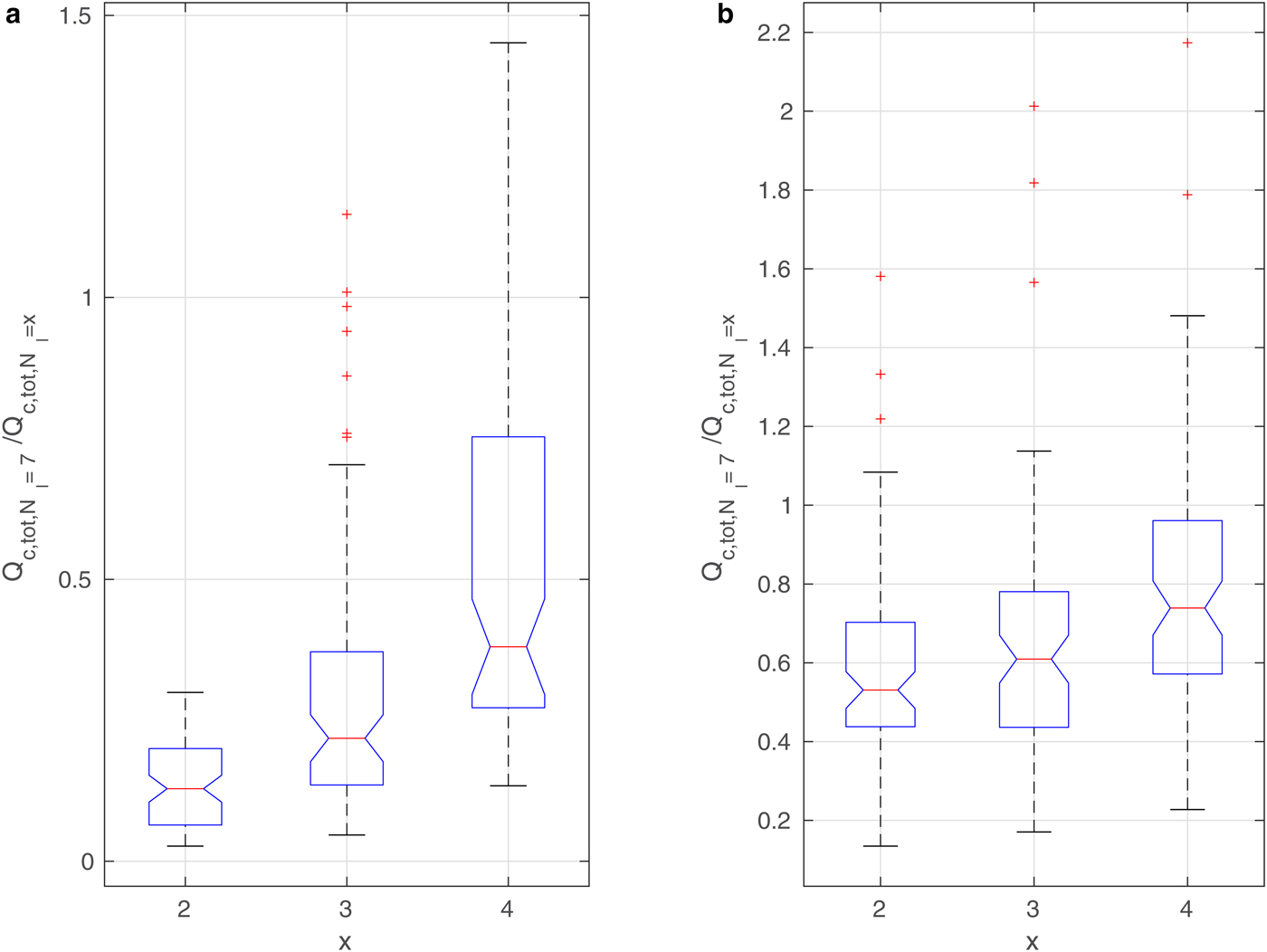
The curves in Figs 9–11 and Supplementary Figs 13 and 14 suggest that in spite of (in some cases, very large) differences in the results, the overall time variability of the analyzed quantities is very similar. In other words, the number of floes or leads in the ice cover modifies the properties of the ABL in a consistent way. In order to demonstrate that this is indeed the case, a box-and-whisker analysis of the ratios of values from the different model runs is performed. In the case of round floes, the model outcome for N f = 5000 is compared with the results for the remaining four N f values (for a given ice concentration c and wind speed profile). Similarly, in configurations with leads, the results for N l = 7 are compared with the three remaining ones (Fig. 12).
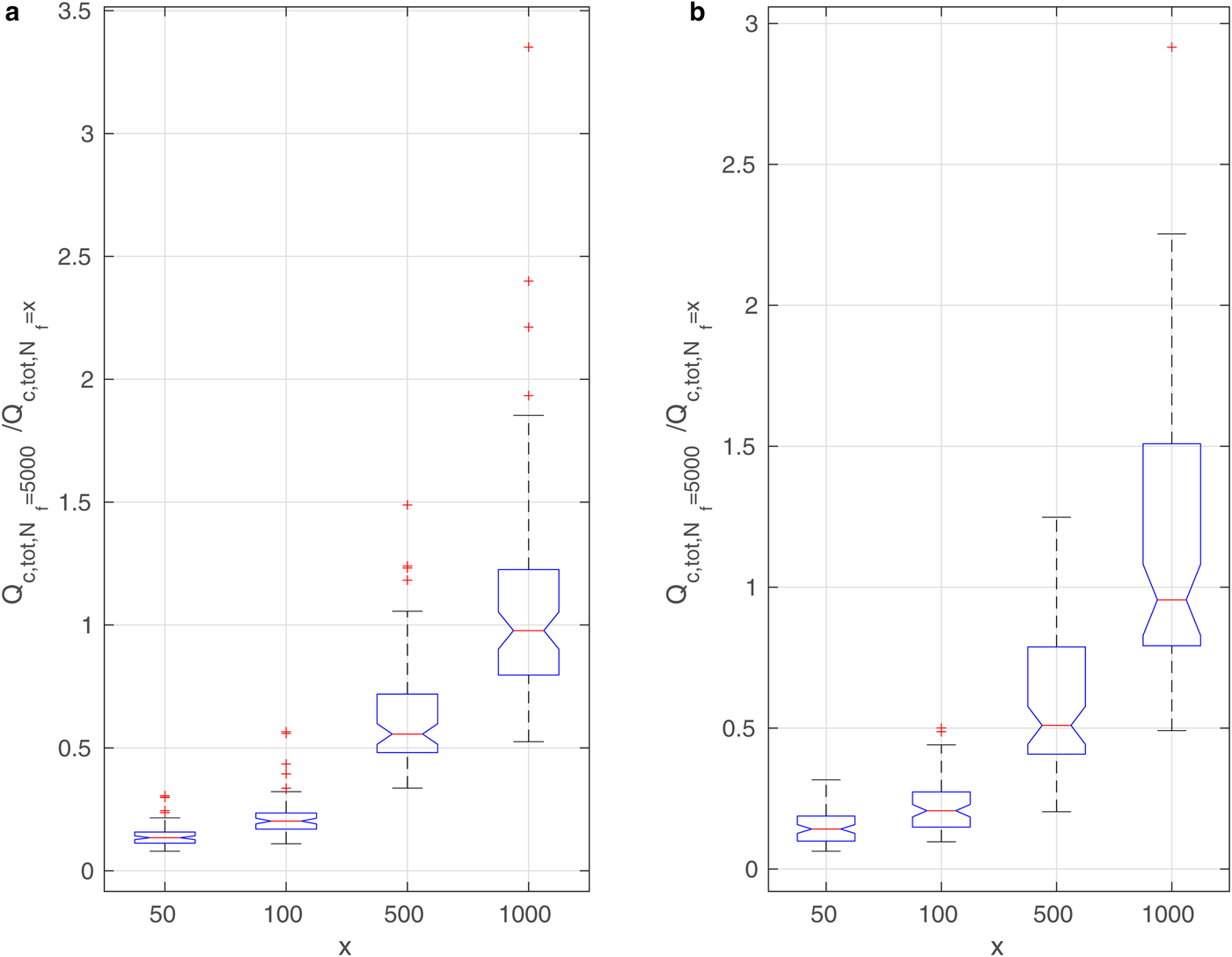
Fig. 12. Box-and-whisker plots for Q c,tot for wind speed profile (a): No. 5 and (b): No. 1 (Fig. 4); ice concentration c = 90%. Each column shows the statistics of all instantaneous values of the ratio ![]() $Q_{{{\rm c,tot}},N_{{\rm f}}=5000}/Q_{{{\rm c,tot}},N_{{\rm f}} = x}$, for x shown in the description of the horizontal axes. Each blue box shows the interquartile range, the red lines mark the median value, and red crosses are outliers.
$Q_{{{\rm c,tot}},N_{{\rm f}}=5000}/Q_{{{\rm c,tot}},N_{{\rm f}} = x}$, for x shown in the description of the horizontal axes. Each blue box shows the interquartile range, the red lines mark the median value, and red crosses are outliers.
The results for total cloud liquid water content (Q c,tot) are shown in Figs 12 and 13 for simulations with round floes and leads, respectively, and for selected ambient wind speeds. Analogous diagrams for F l are shown in Supplementary Figs 16 and 17. We decided to present the influence of a number of floes/leads on the ABL on the basis of those quantities that have already been analyzed in the paper; however, the results are similar for other variables as well. As can be seen, in the case of Q c,tot the values are very different from 1, indicating a strong influence of floe/lead numbers on this quantity. In particular, for N f = 50, Q c,tot is on average ~ 4 times larger than for N f = 5000 for both small and large wind speeds (Fig. 12). In simulations with leads, the differences can be even higher, but they appear more sensitive to wind speed (Fig. 13). Importantly, the scatter of values is not large, and most outliers in Figs. 12 and 13 correspond to the high amount of Q c,tot during the first hour of simulations (model spin-up time) (Supplementary Fig. 13).
The results of the box-and-whisker analysis for the mean turbulent fluxes are not as transparent as the preceding ones. The respective ratios seem to be more strongly dependent on the average wind speed than on the properties of the ice cover. For different N f values, all F l ratios are very close to 1 for the low wind speeds (profile No. 1, 2; Supplementary Fig. 16a). A similar shape of the box-plot diagram is observed for both latent and sensible heat fluxes. However, with the stronger wind the situation changes. With wind profiles No. 4 and 5, the respective ratios vary similarly as in the case of Q c,tot (Supplementary Fig. 16 (b)): the ratios are smallest for N f = 50 and increase with increasing N f, indicating larger heat flux for fewer (and thus larger) floes. However, the values are higher than those for Q c,tot. In simulations with leads (Supplementary Fig. 17), all ratios are close to 1 and no clear dependence on the number of leads can be observed. Nonetheless, those results are once more in agreement with our preceding observations regarding the influence of N l on the turbulent surface fluxes.
Influence of subgrid variability on area-averaged variables
Problem statement
Let us consider two variables (ϕ 1 and ϕ 2, say) characterizing the atmosphere. For the purpose of further discussion, it is useful to write: ϕ i = 〈ϕ i〉 + ϕ′i for i = 1, 2, where 〈ϕ i〉 denotes a value averaged over a certain horizontal domain and ϕ′i is a local fluctuation from that average. In the case considered here, the averaging is performed over the whole model domain, which, as was remarked previously, has a size comparable with the size ΔL of a grid cell of a typical mesoscale weather model. Obviously, in general 〈ϕ 1ϕ 2〉 = 〈ϕ 1〉〈ϕ 2〉 + 〈ϕ′1ϕ′2〉 ≠ 〈ϕ 1〉〈ϕ 2〉 if the covariance between ϕ 1′ and ϕ 2′ does not vanish. As we demonstrate below, due to the presence of convective structures in the ABL over fragmented sea ice, the basic variables describing the state of the atmosphere (air temperature, wind speed, humidity and so on) tend to be significantly spatially correlated. Crucially, the characteristic scales of the convective structures in question are smaller than ΔL. This fact has important consequences for computation of quantities that are nonlinear functions of other variables. Usually, products are computed as 〈ϕ 1〉〈ϕ 2〉, because only grid-scale variables are available. Without information on the subgrid-scale covariance between ϕ′1 and ϕ′2, assessing differences between the estimated value 〈ϕ 1〉〈ϕ 2〉 and the ‘true’ value 〈ϕ 1ϕ 2〉 is not possible.
Surface THF
Computation of the surface THF provides a good example of this problem. The latent and sensible component of this flux, F l and F s, respectively, are typically parameterized as:
where U w denotes the wind speed at 10-m height, T a and q a – the surface air temperature and mixing ratio, T s – the ground surface temperature and q s – saturated mixing ratio at T s. Further, l v denotes the specific latent heat of vaporization, c p – the specific heat at constant pressure and c l, c s are (empirical) transfer coefficients that are spatially variable and depend on the stability of the lower atmosphere. Thus, the area-averaged flux, representative for the scale ΔL, is 〈F l〉 ~ 〈U w(q s − q a)〉 and 〈F s〉 ~ 〈U w(T s − T a)〉, whereas it is typically approximated based on 〈U w〉(〈q s〉 − 〈q a〉) and 〈U w〉(〈T s〉 − 〈T a〉). Below, we analyze differences between the two (for different ice concentration, floe size/lead width and ambient wind speed values) in terms of the coefficients:
The values of α l and α s provide information about the relative error introduced to F l and F s by using area-averaged quantities. This error can be reduced by taking into account subgrid-scale variability of the transfer coefficients, as discussed further in this section (note that in the expressions for α l and α r, the transfer coefficients are not taken into account).
In order to understand the variability of F s and F l in various model configurations, it is useful to analyze the local (small-scale) wind speed and air/surface temperature and humidity differences. Figure 14 shows histograms of U w vs (T s − T a) values from four selected simulations with c = 0.5, with and without wind. Analogous plots for U w vs (q s − q a), as well as for different lead/floe numbers, can be found in Supplementary Figs 18–20. All histograms have two distinct maxima (or, in many cases, consist of two separate point clouds), corresponding to ice and water points. Over ice, almost always (T s − T a) < 0 and (q s − q a) < 0, and the largest amplitudes of these differences (>10°C and > 0.5 g kg−1, respectively) tend to be associated with lowest local wind speeds. Over water, generally (T s − T a) > 0 and (q s − q a) > 0, with typical values in the order of 10–15°C and 1.5–2.5 g kg−1, respectively. This very strong bimodality of T s − T a and q s − q a has very important consequences for area-averaged values of the two components of the THF, F l and F s, especially if the surface areas of open water and ice are comparable (as in our simulations with c = 0.5; Fig. 14 and Supplementary Figs 18–20). The area-averaged humidity and, especially, temperature differences (magenta crosses in the figures) tend to be very small – it is thus a typical situation when the average of many relatively large terms of positive and negative sign is close to zero, and thus very sensitive to changes of those terms.
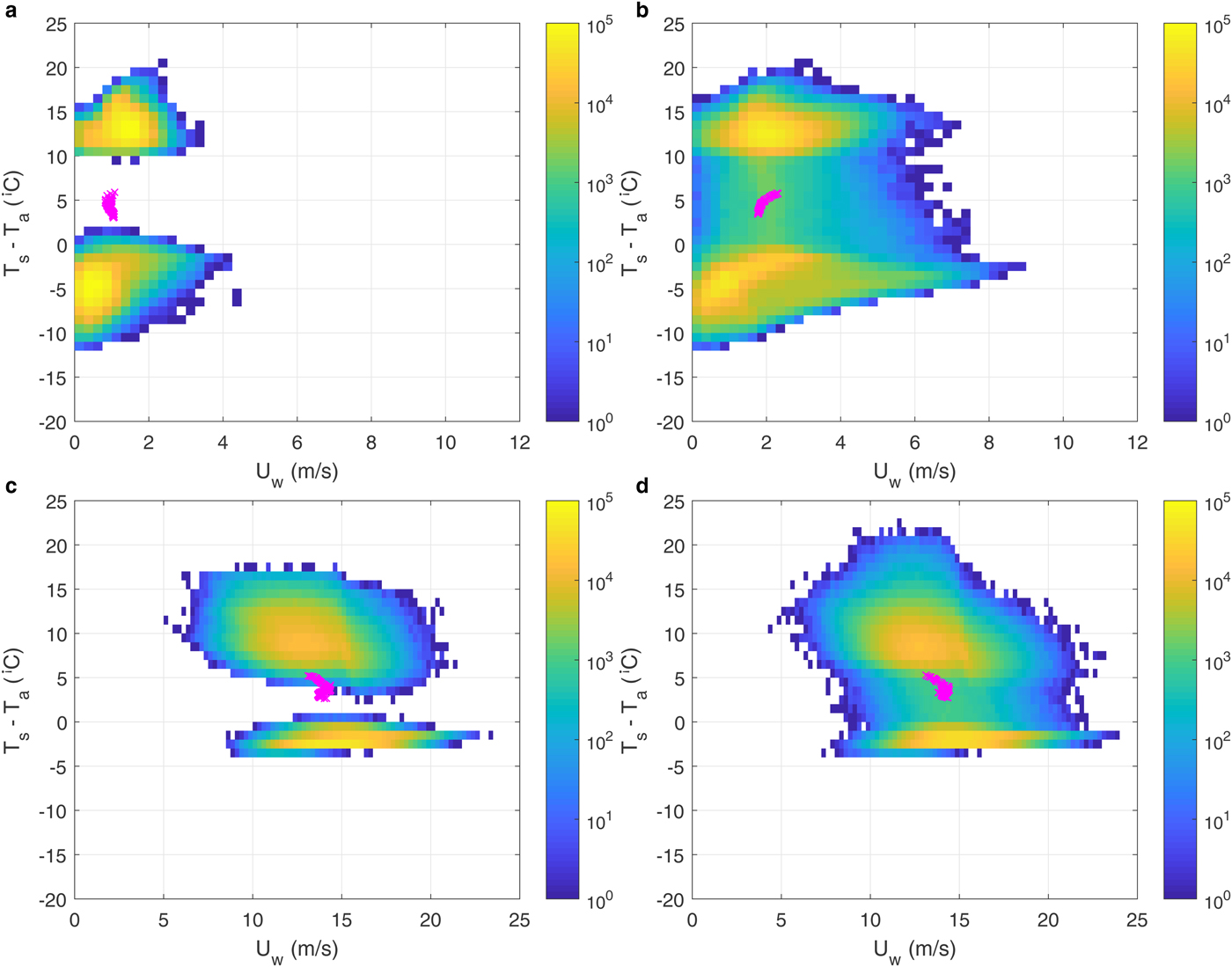
Fig. 14. Histograms of wind speed U w and surface–air temperature difference (T s − T a) for four selected cases with c = 0.5, (a,c): leads, N l = 11; (b,d): round floes, N f = 50; without wind (a,b) and wind profile No. 5 (c,d). Each histogram is based on data from all grid points and times for which results were saved (i.e. every 10 minutes). Bin widths equal 0.25 m s−1 and 1°C, respectively, and the color scale, showing the number of data points within each bin, is logarithmic. Bins without data points are white. Magenta crosses show combinations of area-averaged values (〈U w〉 versus 〈T s − T a〉) throughout each simulation.
In most cases analyzed, the values of F l and F s estimated from area-averaged variables tend to be overestimated relative to their ‘true’ values, especially at moderate ambient wind speeds. The median values of α l and α s are shown in Fig. 15 for different lead/floe configurations and wind speed profiles. Except for very low ambient wind speeds, both α l and α s are larger than 1, and their values are highest at intermediate wind speeds. Importantly, in most cases the scatter of instantaneous values of α l and α s around their respective means is small (Supplementary Figs 21 and 22), suggesting that these values represent stable characteristics of the ABL circulation. It is also worth noticing that at high ice concentration (Fig. 15g and h), the values of 〈T s − T a〉 and 〈T s〉 − 〈T a〉 often are small and have opposite signs, making the computed values of α s meaningless. (In some cases, due to division through a very small number, very large negative values were obtained – see empty boxes in Fig. 15 and in Supplementary Fig. 21.) Thus, using area-averaged values of wind speed and air/surface temperature difference to estimate F s not only leads to overestimation, but often results in an opposite direction of the heat transport. That is, the difference is not only quantitative, but also qualitative, and may lead, for example to false predictions of thermodynamic processes within sea ice. In the remaining situations, α s and α l provide a meaningful estimate of the relative error and their values fall in the range 10–40% of 1.0.
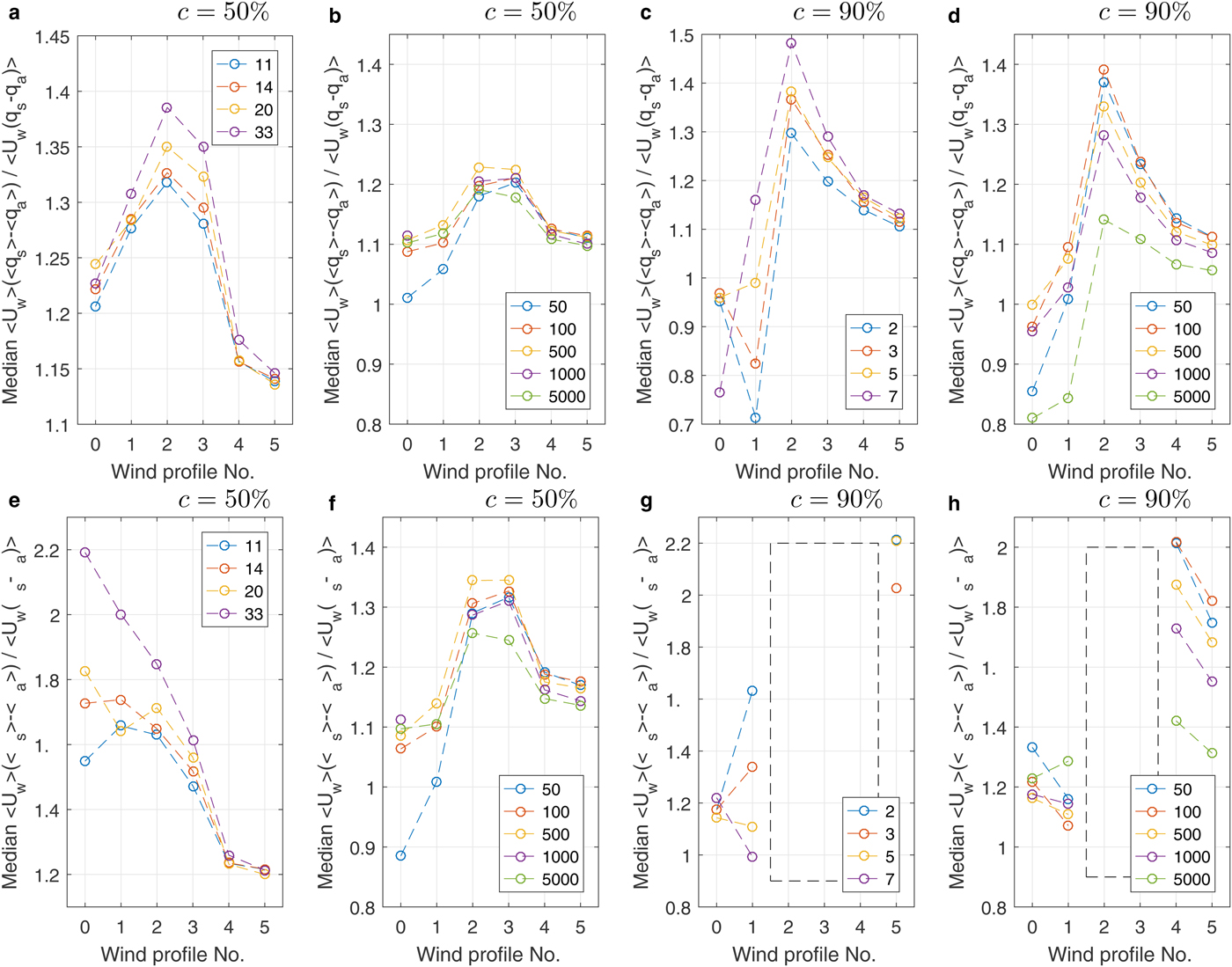
Fig. 15. Median values of the ratio α l (a–d) and α s (e–h) in simulations with leads (a,c,e,g) and round floes (b,d,f,h) for different wind profiles (profile No. 0 means no ambient wind). The ice concentration is written above each plot. Dashed rectangles in (g,h) mark situations in which α s could not be estimated due to different signs of the involved flux values (see text for a description).
DISCUSSION AND CONCLUSIONS
In this paper, the main properties of polar ABL are analyzed in an idealized model setup. We applied various spatial distributions of the sea-ice floes and leads, and different initial wind speed profiles in order to represent a range of possible scenarios. We studied in detail the values of selected domain-averaged quantities (Q c,tot and surface turbulent fluxes) and found the unambiguous dependence of Q c,tot on N f and N l for identical ice concentrations. The three-dimensional air circulation within the model domain varies significantly for different arrangements of leads and floes, depending on ambient wind conditions – showing that the ABL characteristics are sensitive not only to the open water area fraction but also to its spatial distribution. In particular, it has been found that the orientation of leads within sea ice relative to the direction of wind speed may significantly influence the ABL circulation and moisture contents.
Modeling results have not been validated against observational data. In fact, the goal of this work was not to reproduce details of any particular situation, but rather to obtain estimates of the spatiotemporal variability of the ABL processes associated with submesoscale variability of sea-ice properties. Obviously, values of the analyzed quantities may differ considerably between different real-world situations. To date there have been several measuring campaigns that concentrated on the properties of winter ABL over fragmented sea ice, including SHEBA (Surface Heat Budget of the Arctic Ocean; Uttal and others, Reference Uttal2002), AIDJEX (Arctic Ice Dynamics Joint Experiment; Pritchard and others, Reference Pritchard and Robert S.1980) or LEADEX (Lead Experiment; LeadEx Group, 1993) experiments. However, only a few of them (e.g. Ruffieux and others, Reference Ruffieux, Persson, Fairall and Wolfe1995) measured the temperature, heat and moisture fluxes or wind speed simultaneously at a number of locations within a relatively small area, situated at various positions relative to sea-ice features (i.e. over open water, close to floe edges, in central parts of large floes, etc.; for obvious practical reasons, large floes are usually selected as measuring locations). Although there are some exceptions (Uttal and others, Reference Uttal2002; LeadEx Group, 1993) the spatial and temporal resolution of available observational data, for example that from arrays of drifting buoys, typically located many kilometers apart, is frequently not sufficient for this kind of analysis. First, in the case of autonomous buoys the characteristic timescale of the processes in question is usually shorter than or comparable with the time step at which the data are stored (typically a few hours; in dedicated field campaigns the time step can be adjusted to the conditions and processes analyzed, see, e.g. LeadEx Group, 1993; Ruffieux and others, Reference Ruffieux, Persson, Fairall and Wolfe1995; Uttal and others, Reference Uttal2002). Second, differences between data from neighboring buoys may result from both small-scale and larger-scale (mesoscale, synoptic) variability and it is very hard to distinguish between those two effects.
Although other researchers in their modeling studies adopted different approaches to this problem, our results are generally in agreement with them. A direct comparison of the obtained values would be problematic due to differences in applied parameterizations, model schemes, initial conditions and sea-ice properties considered. However, such features as the formation of convective plumes (Burk and others, Reference Burk, Fett and Englebretson1997; Weinbrecht and Raasch, Reference Weinbrecht and Raasch2001), rapid release of heat and moisture (Alam and Curry, Reference Alam and Curry1997; Andreas and Cash, Reference Andreas and Cash1999; Marcq and Weiss, Reference Marcq and Weiss2012), strong local increase of wind speed (Zulauf and Krueger, Reference Zulauf and Krueger2003a) and significant intensification of vertical air motion were reported in other analyses of the Arctic ABL (Shupe and others, Reference Shupe, Kollias, Persson and McFarquhar2008). Furthermore, the generation of convective structures can be observed in the satellite images over fragmented sea ice in early spring or late autumn (Gryschka and others, Reference Gryschka, Drümle, Etling and Raasch2008). Apart from the qualitative agreement, it is worth stressing that the range of variability of the main atmospheric variables in our results is similar to that reported in the above studies. In particular, Tetzlaff and others (Reference Tetzlaff, Lümlpkes and Hartmann2015) and Zulauf and Krueger (Reference Zulauf and Krueger2003a) obtained maximum updraft velocities of ~2 m s−1, close to our results. Therefore, we find it reasonable to assume that our study provides reliable estimates of the range of spatial variability that can be found over fractured sea ice.
Our results clearly show that the spatial distribution of updraft and downdraft regions associated with convective motion within the ABL is related to the underlying features of the ice cover (floes and leads size distribution, etc.). This means that point measurements within the ABL over sea ice might not provide data representative for larger domains (i.e. domain-averaged values might be significantly affected by a small fraction of values strongly deviating from ‘background’). Systematic errors can be expected, dependent on the location of the measuring station relative to the surrounding sea-ice features. In particular, observations in central parts of large ice floes are likely to represent relatively stable conditions typical for surface divergence, with lower wind speeds, temperature and moisture contents than the area-averaged values.
The results presented here suggest a possibility of formulating parameterizations for the coefficients α s and α l for various ambient wind and sea-ice cover ‘types’ (leads, small floes, etc.). This could allow for correction of the transfer coefficients c s, c l in Eqn (1), so that the computed F s and F l would include effects of subgrid-scale structure of the atmospheric circulation within the ABL over ice-covered areas – in a manner similar to that used in the mosaic methods by Vihma (Reference Vihma1995); Arola (Reference Arola1999).
As already mentioned, the formulae (2) and (3) do not include effects related to the spatial variability of the transfer coefficients. Ideally, in large-scale models those functions should account for all effects influencing cell-averaged values of the surface heat fluxes. The problem of biased estimates of heat and momentum fluxes over inhomogeneous surface, related to covariance of the relevant variables, has been recognized and addressed in several atmospheric-modeling studies (e.g. Vihma, Reference Vihma1995; Arola, Reference Arola1999; Andreas and others, Reference Andreas2010; Lümlpkes and others, Reference Lümlpkes, Gryanik, Hartmann and Andreas2012a, and references there). One of the techniques developed in order to reduce those biases and to account for the influence of the subgrid-scale variability of the surface on the cell-averaged heat flux values is the so-called mosaic method (Vihma, Reference Vihma1995; Arola, Reference Arola1999). In this method, heat flux is estimated based on area-averaged atmospheric variables (wind speed, air temperature and humidity) and information on area fraction of a given grid cell covered with particular type of the surface (in the case of a polar ocean, sea ice or open water). In other words, instead of using area-averaged surface parameters, the heat flux is first computed separately for all types of surface occurring within a given grid cell, with different transfer coefficients and only then the cell-averaged heat flux value is computed as a weighted average of surface-type-specific flux values. By adjusting the expressions for the individual transfer coefficients, this method makes it possible to substantially reduce biases related to subgrid-scale variability and covariance of temperature, wind speed and other quantities. Our results clearly show the need for such methods and illustrate the errors that disregarding effects of advection and correlation between the small-scale atmospheric circulation and the underlying surface may introduce. Notably, in our results significant correlation exists not only between the local surface and atmospheric variables, but also within the atmosphere itself (with correlation coefficients between the wind speed and air temperature anomalies in the order of 0.3–0.4). Thus, the empirical algorithms for the transfer coefficients should take into account the fact that, for example the air temperature and wind speed are locally higher/lower than average over open water/sea ice.
Formulating such parameterizations is beyond the scope of this paper, but it is planned for a subsequent study. In general, our results indicate that the submesoscale atmospheric processes over the fragmented sea ice may have significant larger-scale effects which should be examined thoroughly. The enhancement of NWP models with suitable parametrizations of processes analyzed here would likely improve their performance over regions covered with fractured sea ice. We regard this study as a preliminary step to a more detailed analysis and as a source of guidance for further research. In the future, it is our goal to validate the results obtained with field measurements and/or remote-sensing data. In our opinion, collecting data necessary for validation of the model should be possible within one of the large, international measuring campaigns that are planned for the coming years and that include deployment of many autonomous buoys within a relatively small area, within which homogeneous ambient conditions can be assumed. As our study suggests, a number of different variables – wind speed, air temperature, humidity – can be used as a signature of atmospheric circulation within the ABL.
CONTRIBUTION STATEMENT
Both MW and AH planned the research, discussed the results and contributed to their analysis and visualization. MW wrote most of the manuscript, configured the WRF model and performed all computations.
SUPPLEMENTARY MATERIAL
The supplementary material for this article can be found at https://doi.org/10.1017/aog.2018.15.
ACKNOWLEDGMENTS
This work has been supported by the Polish National Science Centre research grant No. 2015/19/B/ST10/01568 (‘Discrete-element sea ice modeling–development of theoretical and numerical methods’). We are very grateful to three anonymous reviewers for very constructive critics and valuable, insightful comments on the first versions of this paper.