Introduction
The Lambert Glacier-Amery Ice Shelf system, -10% of the entire Antarctic ice sheet, is one of the largest glacier/iceshelf systems in Antarctica. It is an important drainage basin in terms of the overall mass balance of the ice sheet and has been the focus of attention for understanding the response of the ice sheet to present and future climate change. The central portion of the system consists of Lambert, Mellor and Fisher glaciers, which drain into the Amery Ice Shelf at its southern limit and then become the central flowbands within the ice shelf (Reference Budd, Corry and JackaBudd and others, 1982; Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007; Fig. 1a). Amery Ice Shelf, with a length of -560 km, has an area of ~60 820 km2 (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). The basin of the three glaciers, i.e. the grounded area of the central portion of the system, which corresponds to the Lambert Glacier basin as defined by Reference RignotRignot (2002), has an area of -0.97 x 106km2 (Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007) and covers -70% of the entire Amery drainage basin. The three glaciers contribute significantly to the mass budget of the Lambert-Amery system (Reference AllisonAllison, 1979; Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010).
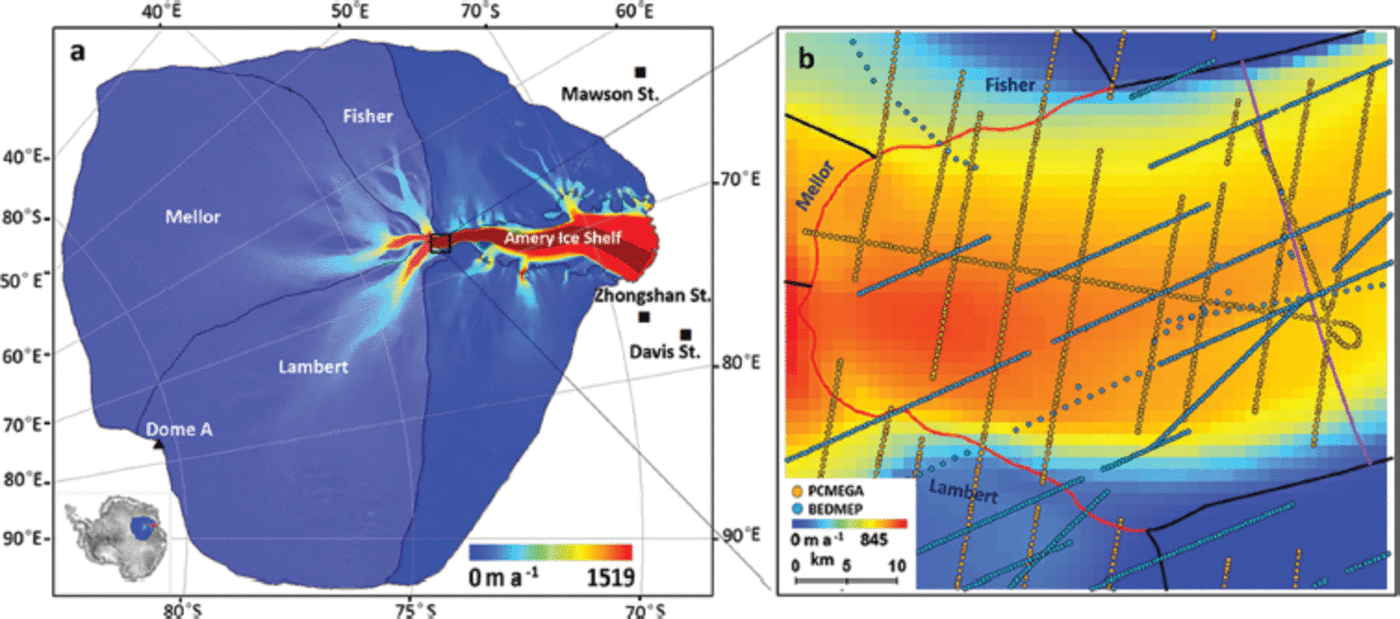
Fig. 1. Maps showing study areas, overlaying a color map showing InSAR surface velocity. (a) The central portion of the Lambert–Amery system, consisting of Lambert, Mellor and Fisher glaciers (in light blue) and their flowbands (in dark red). (b) Ice thickness data from BEDMAP (blue) and PCMEGA (orange) projects in the southern grounding line region of the Amery Ice Shelf. The southern grounding line is shown in red. The G1 flux gate is the pink line.
Several previous studies have focused on the mass budget of the Lambert Glacier basin (e.g. Reference AllisonAllison, 1979; Reference McIntyreMcIntyre, 1985; Reference Bentley, Giovinetto, Weller, Wilson and SeverinBentley and Giovinetto, 1991; Reference Fricker, Warner and AllisonFricker and others, 2000; Reference RignotRignot, 2002; Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007; Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). The most recent three studies (Reference RignotRignot, 2002; Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007; Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010) use similar horizontal ice velocity measurements and the location of the southern grounding line derived by interferometric synthetic aperture radar (InSAR) (Reference RignotRignot, 2002; Reference JezekJezek, 2003, Reference Jezek2008; Reference Fricker, Coleman, Padman, Scambos, Bohlander and BruntFricker and others, 2009; Reference Rignot, Mouginot and ScheuchlRignot and others, 2011). However, the ice thickness data used to estimate ice fluxes through the southern grounding line are from different sources. The ice thickness data used by Reference RignotRignot (2002) and Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007) are estimated from surface elevation data using hydrostatic equilibrium calculations. Those used by Reference Yu, Liu, Jezek, Warner and WenYu and others (2010) are based on a 400 m ice thickness grid interpolated from measurements collected by Australian and Russian aerial radio-echo sounding (RES) surveys during 1968-96, and compiled by the British Antarctic Survey BEDMAP Project (Reference Lythe and VaughanLythe and others, 2001). The total ice fluxes reported for the three glaciers through the southern grounding line of the Amery Ice Shelf are 54.0 ±5.4 Gta–1 (Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007) and 38.9±3.3 Gta–1 (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010) and the reported mass budgets are -2.6 ± 6.5 Gt a–1 (Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007) and 12.6 ± 4.7 Gta–1 (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). The reported basal melt rates near the southern grounding line are 32 ± 5 mice a–1 (Reference RignotRignot, 2002), 31 ± 5 mice a–1 (Reference Rignot and JacobsRignot and Jacobs, 2002), 23.0 ±3.5 mice a–1 (Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007) and 11.4 ±2.8 mice a–1 (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). The above mass-balance estimates are based on similar ice velocity and accumulation data. The substantial discrepancies evident in the estimates are thus due primarily to discrepancies within the ice thickness data and therefore require further examination to reduce the mass-balance uncertainties (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010; Galton-Fenzi and others, 2012). The average ice thickness along the southern grounding line was estimated from hydrostatic considerations to be 2550 m (Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007). The RES average ice thickness, however, is 1291 m (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). Yu and others suggest that the uncertainty associated with the sparseness of RES ice thickness data is expected to be reduced by employing the data from the Prince Charles Mountains Expedition of Germany and Australia (PCMEGA) during the 2002/03 austral summer (Reference DammDamm, 2007).
In this paper, we use ArcGIS to generate a new ice thickness grid over the southern extremity of the Amery Ice Shelf, using the ice thickness data from PCMEGA and BEDMAP, and then combine this gridded ice thickness with a new, high-resolution surface mass-balance (SMB) dataset based on regional atmospheric climate modeling (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012) to reassess the mass budgets of Lambert, Mellor and Fisher glaciers, and the basal melting beneath the Amery ice Shelf. Our final objective is to provide a more precise assessment of the mass balance for the central portion of the Lambert-Amery system.
Data
Our datasets include (1) RES ice thickness data, (2) SMB data, (3) InSAR velocities and (4) grounding line data.
Ice thickness data
The ice thickness data from the PCMEGA aerogeophysical campaign and BEDMAP are used to generate a gridded ice thickness over the southern limit region of the Amery Ice Shelf. The region, 1965.7 km2 in area, covers the confluence of Lambert, Mellor and Fisher glaciers, which drain across the southern grounding line, into the ice shelf (Fig. 1b).
A grid of flight paths spaced 5 km apart, over a total length of 30 000 km and covering an area of ~100000 km2 ranging from 730 S to 77.50 S and 600 E to 700 E was flown during PCMEGA (Reference DammDamm, 2007). A 150 MHz pulse radar was used to measure the ice thickness along the flight paths, with a spacing of 10-15 m between signal reflection points. Vertical resolution in ice is 1, 5 or 50 m, depending on selected pulse length.
A total of 745 original survey measurements of ice thickness for the southern extremity of the Amery Ice Shelf were extracted from the BEDMAP dataset http://www.antarctica.ac.uk//bas_research/data/access/bedmap/ (Fig. 1b). These airborne RES ice thickness data were acquired by the Australian National Antarctic Research Expeditions (ANARE) during 1972/73, 1973/74 (Mission 5) and 1989 (Mission 7) and by the Soviet Antarctic Expeditions (SAE) during 1987/88 (Mission 70), with measurement errors between 30 and 100 m (Reference Lythe and VaughanLythe and others, 2001).
In addition, we use ice thickness grids from BEDMAP and BEDMAP2 to compare with our ice thickness results over the southern limit of the Amery Ice Shelf. In 2001, BEDMAP compiled ice thickness measurements from the Antarctic ice sheet collected prior to the 1990s to generate an ice thickness grid, with a spatial resolution of 5 km (Reference Lythe and VaughanLythe and others, 2001). BEDMAP2 recently presented a new gridded ice-thickness dataset for the Antarctic south of 600 S, using 25 x 106 measurements, over two orders of magnitude more than were used in BEDMAP (Reference FretwellFretwell and others, 2013). BEDMAP2 initially gridded the in situ measurements of ice thickness at 5 km, then the final 1 km ice thickness grid was resampled from the 5 km grid (Reference FretwellFretwell and others, 2013).
Surface mass balance
A new, high-resolution (27 km) SMB dataset for the Antarctic ice sheet is generated, based on output of a regional atmospheric climate model RACMO2.1/ANT, which includes snowdrift physics and is forced by the most recent reanalysis data from the European Centre for Medium-Range Weather Forecasts (ECMWF), ERA-Interim (1979-2010) (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012). The modeled SMB agrees very well with 750 in situ SMB observations (R = 0.88; Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012). The SMB dataset shows low SMB values in large parts of the interior ice sheet (<25 mm a–1).
InSAR velocity
The velocity (Fig. 1) and velocity azimuth measurements used in this study are taken from the processed InSAR velocity database (Reference JezekJezek, 2008; http://bprc.osu.edu/rsl/radarsat/data/) with a gridcell size of 400m. In 2000, three repeat-cycle InSAR data were acquired by a C-band synthetic aperture radar (SAR) sensor on board the RADARSAT-1 satellite during the second Antarctic Mapping Mission (Reference JezekJezek, 2002, Reference Jezek2003), also known as the Modified Antarctic Mapping Mission (MAMM). The RADARSAT InSAR data, covering the area from the Antarctic coast to 82° S (Reference JezekJezek, 2003, Reference Jezek2008), were acquired by a C-band SAR sensor on board the RADARSAT-1 satellite in 2000 (Reference JezekJezek, 2002, Reference Jezek2003). The GPS velocity measurements over the Amery Ice Shelf over the period 1988-99 (Reference KingKing, 2002; Reference King, Coleman, Morgan and HurdKing and others, 2007) were used to compare with the InSAR velocities. The statistics show that the maximum difference between the InSAR velocities and GPS velocity measurements is up to 30 m a–1, and the mean difference is 4.41 ± 9.7 m a–1 (Reference Wen, Wang, Wang, Jezek, Liu and AllisonWen and others, 2010).
Grounding line
The grounding lines of the Antarctic ice sheet have been mapped using satellite visible imagery, altimetry data (e.g. Reference BindschadlerBindschadler and others, 2011) and differential satellite SAR interferometry (DInSAR) data (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011). Here we use the southern grounding line mapping of the Amery Ice Shelf provided by Reference Rignot, Mouginot and ScheuchlRignot and others (2011) using DInSAR data from European Remote-sensing Satellites 1 and 2 (ERS-1/2). DInSAR directly measures the vertical motion of floating ice shelves in response to tidal oceanic forcing with millimeter precision at sample spacing <50m, simultaneously over areas several hundred km wide. This is in contrast to methods that detect abrupt changes in surface slope in satellite visible imagery or altimetry data. The resulting precision of grounding line mapping is 100 m for Lambert Glacier and 300m for Mellor and Fisher Glaciers (Reference RignotRignot, 2002).
Results
Ice thickness interpolation
Ninety-four ice thickness outliers from Mission 7 and Mission 70 were removed manually after cross-validation; the standard deviation (1σ) of these ice thickness data is larger than twice the average standard deviation (196 m) of the total samples. The spatial distribution of the ice thickness measurements is characterized by dense sampling along-track while the flight tracks themselves are widely spaced. Such a distribution poses difficulties for most interpolation techniques and results in a directional bias in the grid (Reference Lythe and VaughanLythe and others, 2001; Reference HerzfeldHerzfeld, 2004). We first generate a net of 500 m x 500 m rectangular cells using a fishnet function of ArcGIS. We then average the coordinates and the ice thickness at all measurement points within each cell, independently for PCMEGA and for BEDMAP (Reference Liu, Wen, Wang, Wang, Csatho and JezekLiu and others, 2007). After data processing, a total of 1226 ice thickness points are retained, including 811 points from PCMEGA and 415 points from BEDMAP. In the confluence region of the three glaciers, the density of ice thickness data points increased significantly (cf. BEDMAP alone) due to the addition of the PCMEGA ice thickness dataset. Before gridding the ice thickness, all data points within the outcrops and nunataks derived from BEDMAP2 products (Reference FretwellFretwell and others, 2013) are set to zero ice thickness and can be used for constructing the ice thickness grid as fixed points for grid interpolations. Finally, the ice thickness data are merged and interpolated onto a 400m cell-size ice thickness grid using ordinary kriging (Fig. 2).

Fig. 2. The ice thickness grid from airborne RES measurements of BEDMAP and PCMEGA, showing the spatial pattern of ice thickness.
Preliminary error analysis is performed using the subsetting and validation tool in ArcGIS. Our 1226 sample points were randomly divided into two groups, including 1128 sample points for a training dataset and 98 points for a test dataset. The training dataset is used to generate an ice thickness grid applying ordinary kriging, and a root-mean-square error (RMSE) of 46 m was calculated by comparing the predictions with the known values in the test dataset.
Ice thickness characteristics
From Figure 2 several features can be observed. The thickest ice in the region is 2790m, within the Mellor Glacier flowband of the ice shelf, and the thickest ice along the southern grounding line is 2760 m, at the transition zone of Mellor Glacier with the floating ice shelf. Of the three glaciers, Mellor and its flowband is thickest, mostly up to 2000 m, with some areas as thick as 2500 m. The ice thickness increases rapidly downstream of the Lambert Glacier/ice-shelf grounding line, from 1000-1500 to 1500-2000m.
A comparison of the ice thickness along the southern grounding line as indicated by the combined BEDMAP + PCMEGA dataset with that indicated by BEDMAP alone shows that the combined dataset indicates Fisher Glacier is -0-500m thicker than indicated by BEDMAP, Mellor Glacier is ~300-1000 m thicker and Lambert Glacier is ~0-500 m thinner (Fig. 3). The ice thickness variability in the combined dataset is greater than that of BEDMAP, and more ice thickness detail along the grounding line is evident in the combined dataset. In contrast, a comparison of the ice thickness produced by the combined BEDMAP+PCMEGA dataset with BEDMAP2 shows that both datasets have a similar variation trend along the southern grounding line (Fig. 3), though the difference between the two datasets is still large (>300m in some sections). This may be attributed to the different interpolation methods: BEDMAP2 initially gridded the in situ measurements of ice thickness at 5 km, then resampled the 5 km grid to a 1 km grid (Reference FretwellFretwell and others, 2013).
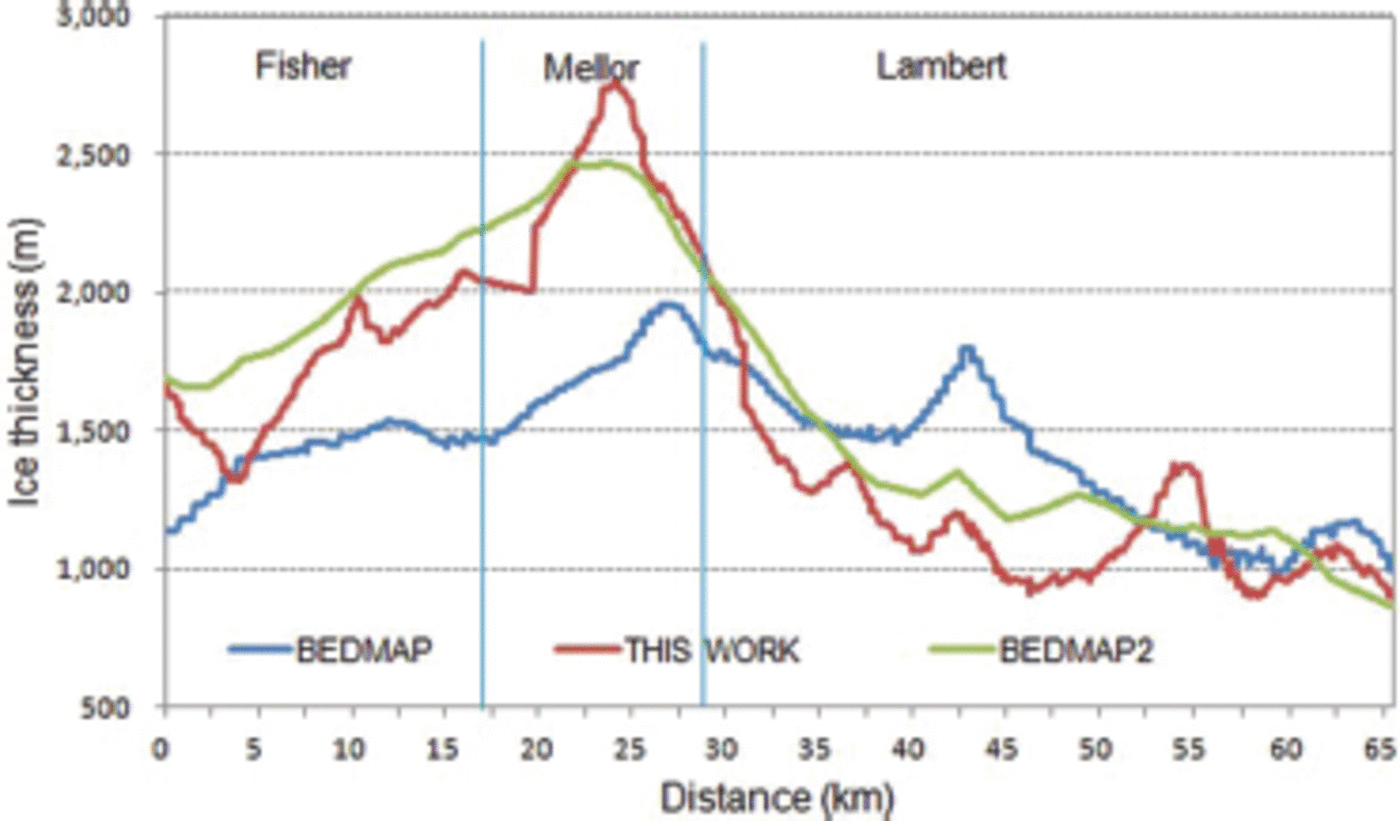
Fig. 3. Comparison of the ice thickness along the grounding line as indicated by the combined BEDMAP + PCMEGA dataset with BEDMAP and BEDMAP2 alone.
Mass budget of individual glaciers and of Lambert basin
We use the component approach (ISMASS Committee, 2004) to assess the mass budget and basal melting of the central portion of the Lambert-Amery system. We use velocity magnitude and azimuth data at 400 mx400m spacing from the MAMM project (Reference JezekJezek, 2003, Reference Jezek2008) and resolve them normal to the grounding line. Ice volume flux F through the southern grounding line is calculated as the product of mean ice velocity and mean ice thickness at the grounding line (Reference Wen, Jezek, Monaghan, Sun, Ren and HuybrechtsWen and others, 2006):
where H is the ice thickness, U is the surface ice velocity, w is the distance across the gate, K= sin Φ is a correction factor applied to convert the velocity to its equivalent value normal to the gate (Φ is the angle between the gate and the ice flow direction) and R is the velocity ratio, which is assumed to be 1 along the grounding line where basal sliding makes up a substantial fraction of the column-averaged velocity (Reference HuybrechtsHuybrechts, 2002). The ice density (914 kg m–3) is used to convert the ice volume flux to mass flux.
The total snow water equivalent accumulated over the area upstream of the grounding line is estimated using the SMB dataset for the Antarctic ice sheet based on output of a regional atmospheric climate model RACMO2.1/ANT (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012). The differences between the accumulation (input) and the flux (output) are the mass budgets of the areas (in this case, Lambert Glacier, Mellor Glacier, Fisher Glacier and the total, which is equivalent to the Lambert basin; Table 1). Ice fluxes for the glaciers and the Lambert basin, based on BEDMAP2 (Reference FretwellFretwell and others, 2013), hydrostatically derived ice thickness (Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007) and BEDMAP (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010), are also listed in Table 1 for comparison.
Table 1. Accumulation, ice flux and mass budget for Lambert, Mellor and Fisher glaciers, and for the total (Lambert basin)
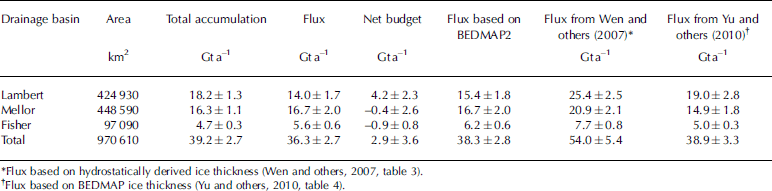
Our ice fluxes through the grounding lines of Lambert, Mellor and Fisher glaciers and of the Lambert basin as a whole are close to those of Reference Yu, Liu, Jezek, Warner and WenYu and others (2010) and those based on BEDMAP2, except that our flux for Lambert Glacier is significantly less than that of Reference Yu, Liu, Jezek, Warner and WenYu and others (2010) (Table 1). Our total surface accumulations for Lambert, Mellor and Fisher glaciers and over the Lambert basin as a whole are significantly less than those of Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007, table 3) based on the average of the Vaughan and Giovinetto compilations (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999; Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000), and those of Reference Yu, Liu, Jezek, Warner and WenYu and others (2010, table 2) based on Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999). For example, our total surface accumulation for the Lambert basin (39.2±2.7Gta–1) is only about two-thirds (51.4±3.6 and 51.6±2.6Gta–1) those of Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007) and Reference Yu, Liu, Jezek, Warner and WenYu and others (2010) respectively. The results indicate that Mellor and Fisher glaciers are approximately in mass balance to the level of our measurement uncertainty, while Lambert Glacier is in positive imbalance. The three glaciers as a whole (Lambert basin), with a net mass budget of 2.9±3.6Gta–1, are approximately in mass balance to the level of our measurement uncertainty.
Table 2. Basal melting for the central flowband of the Amery Ice Shelf

Basal melting estimates for the central flowband of the Amery Ice Shelf
Wen and others (2007) placed 18 flux gates along the Lambert, Mellor and Fisher flowbands, and estimated the basal melting and refreezing along the central flowband in detail. Here we use flux gates GL (the southern grounding line), G1 (~40 km downstream of the southern limit of the grounding line; Fig. 1b and 2) and G18 (~10 km south of the ice-shelf front; fig. 2 of Wen and others, 2007) to provide an estimate of basal melting near the confluence of the three glaciers at the southern grounding line, and along the central flowband of the ice shelf. Reference KingKing and others (2009) suggest the Amery Ice Shelf has been relatively stable over four decades since 1968. In a similar fashion to Reference RignotRignot (2002), Reference Rignot and JacobsRignot and Jacobs (2002) and Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007, Reference Wen, Wang, Wang, Jezek, Liu and Allison2010), the snow accumulation input and ice fluxes through the southern grounding line and the gates deployed over the ice shelf are used to estimate basal melting or refreezing, assuming the ice shelf is in a state of mass balance. The ice density (914 kgm–3) is also used to convert the ice volume melting to mass melting.
Net basal melt amount and average melt rate for the two sections (GL-G1 and G1-G18) of the ice-shelf central flowband and as a whole are presented in Table 2. The total basal melt amount in the region between the southern grounding line and flux gate G1 is estimated to be 5.4 ± 3.1 Gta-1, and the average melting rate is 5.1 ±3.0ma–1 (Table 2). This melt rate is - 2 5% of the value (21.0 ± 3.2 m a–1) calculated by Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007), and <20% of the value (31 ± 5 ma–1) calculated by Reference Rignot and JacobsRignot and Jacobs (2002). Our net melt rate between G1 and G18 is 0.7±0.1 ma–1, which is close to that estimated using the data from Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007). The average melt rate of the whole central flowband of the Amery Ice Shelf is 0.9 ± 0.1 m a–1, less than estimated (1.8 ± 0.3 m a–1), using the data from Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007). We believe the differences in these results are primarily caused by the substantially different ice thickness values used along the southern grounding line; previous studies used hydrostatically derived ice thickness data.
The error sources in our mass-balance estimates include uncertainties in accumulation and ice flux. We assume a 5% accumulation rate error and 5% area error (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). The estimated accuracy of the ice velocity data is ±10 m a–1 (Reference JezekJezek, 2003, Reference Jezek2008); the mean difference between the InSAR velocities and the GPS velocity measurements is 4.41 ± 9.7 m a–1 (Reference Wen, Wang, Wang, Jezek, Liu and AllisonWen and others, 2010). The uncertainty of the velocity azimuth is 3° (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). The ice thickness error from PCMEGA is up to 50 m (Reference DammDamm, 2007) and BEDMAP error ranges from 30 to 100 m (Reference Lythe and VaughanLythe and others, 2001; Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010). Our ice thickness grid has an RMSE of 46m, estimated by comparing the predictions with the known values in the test dataset. The errors in the ice flux, mass budget and basal melting estimates are quantified, based on statistical theory of error propagation (Reference TaylorTaylor, 1997; Tables 1 and 2).
Discussion and Conclusion
Our analysis indicates that the ice flux through the Amery Ice Shelf southern grounding line is 36.3 ± 2.7 Gt a–1, which is close to the value (38.9±3.3Gta–1) of Reference Yu, Liu, Jezek, Warner and WenYu and others (2010), but much less than that (54.0±5.4Gta–1) of Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007). Mellor and Fisher Glaciers are approximately in mass balance to the level of our measurement uncertainty, while Lambert Glacier has a positive imbalance of 4.2 ±2.3 Gta-1. The overall mass budget (2.9 ± 3.6 Gta–1) for the Lambert Glacier basin is approximately in mass balance to the level of our measurement uncertainty, which is similar to the result of Reference ShepherdShepherd and others (2012, fig. 1), who used the same SMB dataset as Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others (2012). The overall mass budget for the Lambert Glacier basin is also similar to the results of Reference RignotRignot (2002), Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007) and Reference RignotRignot and others (2008), but previous total snow accumulations and ice fluxes across the southern grounding line are much larger than those used in this study. The overall mass budget for the Lambert Glacier basin is different from the result of Reference Yu, Liu, Jezek, Warner and WenYu and others (2010) who found a significantly positive imbalance. This is because the new SMB dataset (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012) indicates lower net snow accumulation over the Lambert basin than that of Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999), and used by Reference Yu, Liu, Jezek, Warner and WenYu and others (2010). Based on satellite remote sensing and field-gathered datasets, Reference ScambosScambos and others (2012) found that there is a large extent of near-zero net surface accumulation ‘wind glaze’ areas on the East Antarctic plateau, resulting from persistent katabatic winds. Studies of SMB (e.g. Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999; Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000) interpolate values across glaze regions, leading to overestimates of net mass input. Of three recent models of Antarctic SMB, the lowest-input model (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012) appears to best match the mean in regions of extensive wind glaze (Reference ScambosScambos and others, 2012). The Lambert Glacier basin has a large percentage (19.1%) of glaze area above 1500 m elevation, leading to a much lower total snow accumulation than previous estimates (e.g. Reference RignotRignot, 2002; Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others, 2007; Reference RignotRignot and others, 2008; Yu and others, 2010).
The average melt rate for the region between the southern grounding line and flux gate G1 is 5.1 ± 3.0 m a–1, which is less than the estimate (10.4±2.4ma–1) of Reference Yu, Liu, Jezek, Warner and WenYu and others (2010) and less, by 20-25%, than the results of Reference RignotRignot (2002), RReference Rignot and Jacobsignot and Jacobs (2002) and Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007). The differences are primarily caused by the use of different ice thickness datasets at the southern grounding line flux gates, where both Reference RignotRignot (2002) and Reference Wen, Jezek, Csatho, Herzfeld, Farness and HuybrechtsWen and others (2007) used hydrostatically derived ice thickness data while we (and Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010) used RES ice thickness measurements. Because of ice flexure due to tidal movement at the grounding zone, the hydrostatic equilibrium condition between elevation and ice thickness is not satisfied in the confluence zone (Reference Fricker, Coleman, Padman, Scambos, Bohlander and BruntFricker and others, 2009). The hydrostatic method may therefore overestimate ice thickness in this zone (Reference Yu, Liu, Jezek, Warner and WenYu and others, 2010), resulting in high ice flux estimates. Our study combines the RES ice thickness data from BEDMAP and PCMEGA to generate a digital ice thickness grid over the Amery Ice Shelf southern grounding zone region, to further reduce the uncertainty in the ice thickness data used by Reference Yu, Liu, Jezek, Warner and WenYu and others (2010).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (grant No. 41276188) and National Basic Research Program of China (grant No. 2012CB957704). We thank J.T.M. Lenaerts for providing SMB data, Jaehyung Yu and Hongxing Liu for providing the interpolated ice thickness grid and T.A. Scambos for valuable comments. Constructive comments and suggestions from two anonymous reviewers have been very helpful in improving this paper.







