Distribution of Snow Drifts on Ridge Slopes: Measurements and Theoretical Approximations

Abstract

During several winters the positions and magnitudes of excess snow deposits or denudation zones caused by wind have been evaluated on the flanks of regular, elongated mountain ridges. The surveys were carried out by conventional measurements of mass balance. According to angle of slope (10 to 35°), shape of crest (hump- or wedge-shaped) and orientation to the wind, various patterns of snow deposition may be found. It is shown that, on ridges oriented perpendicularly to the main wind direction (north-west) during snow storms, near-periodic snow deposits may be expected on the lee slope. On the windward side, there is a denudation zone near the crest. The measurements indicate that lee slopes, of mean slope angle, are buried in mid-winter under twice as much snow as the adjacent windward slopes. However, the ridge system as a whole accumulates the same amounts of snow as do areas of flat terrain. Theoretical approximations based on theories of potential flow and semi-empi rical plume models are used to simulate the presumed dispersion of snow. The model calculations, intended as diagnostic tools, suggest that snow may be diffused and deposited on lee slopes in a plume-like manner similar to other particulate matter. Snowfall, together with low-level blowing snow as an additional source of suspended particles, appears to increase the snow deposits, mainly on the foot of steeper ridges.

Introduction

Positions and magnitudes of zones of excessive deposits of snow on lee slopes, or areas of snow erosion on windward slopes, are important for management of avalanches, ski slopes, and snow hydrology. Whereas avalanche forecasters and watershed hydro-logists are mainly interested in a mean areal surplus snow deposit per storm sequence or winter period, people dealing with the details of avalanche formation and the possibilities of artificial release, and with ski-slope management would also like to know the probable position of snow drifts and erosion zones.

Basic knowledge about the processes of formation of such zones is still poor, because previous measurements on cause (wind field, snowdrift flux) and effect (areal snow accumulation) were insufficient. In past years, most attention has been given to the microscale “pick-up” process of snow particles and their subsequent surface-bounded transport (cf. Schmidt 1980, Schmidt and Randolph 1981). A few studies treated the aspect of interaction of snowdrift flux and terrain, including Tabler (1975), Dyunin and Kotlyakov (1980), and Schmidt and Randolph (1981) of which the first-named is the most rewarding from a practical viewpoint. Based on the principle of of maximal equilibrium depths of snowdrifts behind small hills and ditches, Tabler's work yields empirical formulae to quantify the final snow deposits along such terrain features. These findings may not be transposed to larger mountain ridges, because the snow cover in that situation never reaches equilibrium depth during the course of one winter, but they they may serve as useful design criteria in appropriate locations (hills of height H<20 m).

In this paper, we shall investigate general patterns of snow deposits on the slopes of elongated mountain ridges. Because the turbulent flow over mountain ridges is highly complex, there is no current theory to explain, a priori, the diffusion and deposition of suspended snow around such ridges. Therefore our study is divided into two parts. (1) Analysis and interpretation of areal snow-cover measurements at ridge locations in order to find overall deposition and, hence, flow characteristics. Knowledge about existing general features may be useful for practical applications as well as for theoretical developments. (2) Development of a few theoretical approximations to explain the measured mass distribution under given atmospheric conditions. No attempt is made so far to simulate numerically the complex flow field by using finite-difference techniques.

Field Observations and Measurements

In the early seventies, areal surveys of snow-pack stability along ridge crests showed us that snow accumulation is usually very uneven, depending on the orientation of ridges and the main direction of the wind. The well-known cornice, often visible till late spring, may serve as an index, but other more important features are not revealed by visual inspection. In an earlier report (Föhn 1980) a few measurements, mainly around crest-line locations, were presented but it was obvious that these measurements were not sufficient to discuss the existing flow and deposition phenomena on a general basis. In the last few years additional measurements have been executed, including some in other ridge locations.

Locations and ridge shapes

The surveyed ridges are all situated in the vicinity of the Eidgenössiches Institut für Schnee-und Lawinenforschung, Weissfluhjoch (2 670 m a.s.l.), Switzerland. Because the three-dimensional problem is so difficult, all surveyed ridges were elongated (two-dimensional) and with as regular slope surfaces as possible. However, it may be noted here that the requirement of shape regularity, elongation, and appropriate crest-line orientation is a requirement which could not be fully attained.

The ridges were of varying sharpness, with apex angles between 110 to 160° and slope angles between 10 and 35°. This might be regarded as quite typical for our Swiss Alpine topography. Ridges with slope angles steeper than 35° were often not accessible in mid-winter because of severe avalanche danger. Cross-profiles of the terrain of the two most intensively surveyed ridges are shown in Figures 1 and Figures 2.

Fig. 1. Cross-profile of Gaudergrat, Switzerland, and mean areal snow distribution over the ridge as a projection of values of water equivalents on the ridge base line (in mm or kg m⁻²) on selected dates in winter 1978-79.

Fig. 2. Cross-profile of northern Schwarzhorngrat, Switzerland, and mean areal snow depth over the ridge as base line projection on selected dates of winter 1980-81.

Measuring Procedures

The volume or mass of snow was determined by using conventional survey techniques. By combining cross-profiles of soundings of snow depths HS in equidistant lines roughly 20 m apart with density measurements obtained from core samples, the snow mass or water equivalent WE of the deposit was determined. By performing such measurements before and after a major snowstorm, the recently deposited snow mass ΔWE could be evaluated and mapped. Snow-depth soundings were taken every 2 to 4 m along the lines. Thus, every field study resulted in 600 to 1 000 data points, depending on the stretch of ridge surveyed. Since snow density is rather a conservative variable, only a few point measurements have been made for each survey. If the density measurements showed little variation along the lines, snow depth was often used as a measure of snow mass.

Results and Discussion

Before we proceed to the interpretation of results, we have to explain some basic points. A lee slope is a ridge slope which, in general, receives more snow than the surrounding, flat terrain; in our climate, the aspect of a lee slope is mainly east. Windward slopes usually face west and receive less snow. However, on a few occasions each winter, minor snowstorms move into the region from the opposite direction, reversing the drift flux and smoothing over drift features created by the main west or north-west wind in previous periods. Limited space for presentation forces us to restrict our discussion to a few data curves even though other un-reported measurements helped us to derive the following patterns of deposition.

Figures 1 and 2 show the mean area 1 distribution of snow mass WE or snow depth US on two ridges on various dates. The following points may be observed. Snow is very irregularly distributed where it is near the ridge crest. This pattern becomes more evident as the winter progresses. Windward slopes show denudation of snow in the upper part and lee slopes accumulate surplus snow. Lee slopes of angles greater than about 25° and with a crest edge towards the lee side show a sharp cornice which grows steadily by accretion with each storm. Further downslope, a large depression of the snowpack is often observed, which recovers towards the foot of the ridge. A secondary smaller maximum of snow depth is situated at the ridge foot. Thereafter, snowpack depth returns to the normal values of level reference plots.

The northern part of Schwarzhorngrat is fairly regular, as shown in Figure 2. In its southern part, the crest line slopes gradually down until the ridge resembles a small hill. This gave us the opportunity of observing accumulation and erosion features on rather flat, hump-shaped hills. Figure 3 shows a map of the terrain configurations and the distribution of snow mass in midwinter. It can be seen that small differences in terrain cause large effects in snow deposition and that only areal mean values (measured along the ridge slopes as given in figures 1 and 2) yield representative patterns of deposition. As may be seen from the map, or more clearly from Figure 4, the shape and sharpness of the ridge influences the patterns of accumulation and erosion very strongly. Figure 4 shows cross profiles of snow depth over the same ridge at three locations with decreasing ridge heights and reduced apex angles. Whereas the top profile (Nr.11) is still similar to the ones discussed in figures 1 and 2, the lower ones (Nrs.5 and 1) indicate substantial changes, especially in the pattern of snow accumulation on the lee slope. Mr.5 already indicates a retrogression of the first snow depth maximum downslope and in Nr.l this snow depth maximum is clearly detached from the crest line. Finally, comparing the distribution of snow mass in the map (Fig. 3) and the corresponding snow-depth profiles of Figure 4, we observe that the depression on the lee side only exists as long as H/L~>0.5, where H represents the height of the ridge and L the length of the base of the lee slope. Possible explanations for these features are given in the next section on the basis of some model calculations.

Fig. 3. Map of Schwarzhorngrat (scale - 1:3 000) with areal pattern of snow mass (mm or kg m⁻² of water) at midwinter 1980-81. Note also position of snow-depth cross-profiles Nrs.l, 5, 11, represented on Figure 4.

Fig. 4. Three typical snow-depth cross-profiles on Schwarzhorngrat in midwinter 1980-81, showing the dependency of pattern of snow deposition on ridge shape and slope angle. Snow depth is shown true to scale along the ridge slopes and as a base-line projection.

figures 5 and 6 yield some insight into the temporal distribution of snow mass between windward and lee slopes for Gaudergrat and Schwarzhorngrat. The dashed lines represent the mean increase of snow mass M of the whole ridge area surveyed in water equivalents, i.e. the arithmetic mean of the windward and lee slope areas. It merely shows the increasing snow mass during winter-time. The additional dashed-dotted line yields a comparison between the above areal ridge mean M and a nearby reference plot R on flat ground of similar elevation where snow accumulation is mainly influenced by precipitation. The course of the line around a ratio value M/R = 1 documents that such ridge systems catch, as a whole, the same amounts of snow during winter as do so-called representative flat fields in the vicinity. Snow mass is transferred only from the windward to the lee slope by processes of snow transport. However, the comparison between data from Gaudergrat and Schwarzhorngrat indicates that ridges projecting higher into the air stream (Gaudergrat) may lose some snow, probably further down-wind (5 to 10% according to Figure 5), when compared to smaller ridge systems such as the Schwarzhorngrat.

Fig. 5. Snow water equivalents from Gaudergrat during one winter. The dashed line represents the course of the arithmetic areal mean M (units are indicated at the right ordinate). The solid line shows the ratio between lee and windward slopes: L/w (units are indicated at the left ordinate). The dashed-dotted line shows the ratio between the arithmetic areal mean and the flat reference plot M/R (units are indicated at the left ordinate).

Fig. 6. Snow water equivalents from Schwarzhorngrat during one winter. The dashed line represents the course of the arithmetic areal mean M (units are indicated at the right ordinate). The solid line shows the ratio between lee and windward slopes L/W (units are indicated at the left ordinate). The dashed-dotted line shows the ratio between the arithmetic areal mean and the flat reference plot M/R (units are indicated at the left ordinate).

The displacement of snow from the windward to the lee slope is traced by the solid line in figures 5 and 6. This line corresponds to the mean areal snow mass ratio L/W of lee slope L to windward slope H. The temporal mean values of 1.5 to 2 over the winter illustrate the fact that in the Swiss climate, typical lee slopes may be huried under a snow load twice as large as the opposite windward slopes. The whole range of measured ratios L/W over four winters covers the span 1.1<L/W<2.7, with a mean value of 1.63. If the wind direction during snowstorms is almost exclusively west or north-west, we observe an increase of the L/W ratio towards the end of winter; otherwise, in a normal winter such as the one represented in figures 5 and 6, no marked trend is visible.

Other sources than snow drifts, which could also influence the ratio of snow mass between the two slope aspects, are negligible in our case: occasional meltwater will be trapped in the lower layers of the snowpack until the end of April, and evaporation and sublimation losses are small during drift-free periods (ΔWE ≈ 6 mm per month) and would have the same order of magnitude on lee and windward slopes.

Theoretical Approximations of Cross Flow and Smovj Deposits on Lee Slopes

Searching for explanations of our near-periodic snow deposits behind elongated ridge crests, we are forced to quantify snow-laden airflow and deposition on the ground. Since the pattern of deposition shown in Figures 1 to 4 originates mainly from northwesterly snowstorms containing upper-air deflection of precipitating snow crystals and surface-bounded blowing snow, we have to consider both processes. At present, boundary-layer airflow combined with snow flux cannot be solved analytically over complex terrain. Thus we use a simple potential flow model to simulate the upper-air snow flux and a so-called plume model to describe the surface-bounded snow plume along an extended slope of given shape. The model assumptions and notations are represented in Figure 7. The models are intended as diagnostic tools rather than as time-dependent predictive models, because the initial data fields and the boundary conditions are based only on observed mean values or other assumptions that are generally justifiable.

Fig. 7. Schematic representation of snow deposition and model assumptions and notations: (a) general course of snow deposition pattern on ridges and their snow-mass means, (b) notations of potential flow model and resulting snow deposition, (c) notations of plume model and resulting snow deposition.

Potential flow

During a snowstorm, precipitating snow particles are fed into the air-stream crossing a ridge crest upwind of the crest. Air flow and snow flux are approximately horizontal above the crest. Assuming twodimensional, steady-state, potential flow over the ridge crest ((b) in Fig. 7), the equation of conservation of mass may be written

(1)

where c and u are snow concentration and air-snow velocity respectively, is the streamtube cross-sectional distance and s the streamline. Defining additionally an upper limit of disturbance of the air layer H’ and the hump-shaped ridge of form h(x) = a²/(b² + x²), we may formulate the expansion flow depth p(x) along the lee slope by

(2)

Consequently, the mean local velocity u(x) above the terrain may be expressed on the basis of Equation (1) by

(3)

where u₀ is the mean flow speed above the crest line. If a snow particle had zero fall velocity the potential flow position of the particle would be given by the expression

(4)

with the aid of Equation (3) the mean travel speed u_x of the particles can be found to be

(5)

If v_s is the actual fall velocity of a snow particle due to gravity the vertical displacement of the corrected vertical position of the particles is then given by

(6)

V_s may be taken as constant for these small particles. According to Businger (1965) we may formulate

(7)

Particle trajectories and streamlines are no longer identical and the boundary condition z’(x) = h(x) decides where a particle hits the terrain surface.

For the case of pure precipitation flux over the crest, assuming a constant particle concentration c0 over H'-h(O) and a constant flow speed u0, we may approximate the lee-slope snowfall deposition per horizontal interval Ax in a given time span Δt:

(8)

Δ is the chosen height interval for which the step-wise simulation is executed. The principal notations, the lowest streamlines and trajectories, and a resulting deposition pattern are represented by (b) in Figure 7.

The main assumptions were as follows: H' = twice the ridge height H, u_o = 10 m s⁻¹, c_Q = 0.1 g m⁻³ (a moderate snowfall concentration), d = 0.3 mm, p* = 500 kg m⁻³, and C_D = 1.66 (List 1971).

The pattern of the resulting rates of deposition (over several days) shows that precipitating particles are mainly distributed at the foot of ridges when the initial snow concentration above the ridge is uniform. In order to visualize the effect of a mixture of rather large particle sizes in the crest concentration the following particle distributions have also been simulated:

The results of this simulation are represented in Figure 8 and show that, while snow is deposited increasingly towards the foot of the ridge, the deposit is less pronounced than that shown in (b) in Figure 7 due to the increased contribution of larger, faster depositing particles.

Fig. 8. Trajectories of snow particles of typically varying fall velocities in a potential flow field and corresponding rate of snow deposition along hump-shaped lee slope.

Plume model

The diffusion of a narrow, surface-bounded, snowdrift flux downwind from a ridge crest is a typical problem of wake diffusion. Since we have no measurements about the wake flow characteristics, beside the resulting pattern of snow deposition, and because little is known about this problem, we decided to use a plume model approach, based on the early theoretical work of Sutton (1953). The equation used is the steady-state Gaussian plume equation, described by Pasquill (1974). In a near-neutral, turbulent atmosphere it is commonly assumed, and has been confirmed, that plume matter (snow) spreads horizontally and vertically from the centreline in a Gaussian concentration profile. For a continuous band source at the crest line the snow concentration at the ground surface may be written

(9)

wnere H is the ridge height, h' the plume height above the crest line (derived from X.tan α/cos²Ψ where a is the plume slope of 6.3°, derived empirically by Pasquill (1974), Ψ is the angle of the windward slope, and X is the horizontal length of the observed windward erosion zone), and H + h'/2 is the source height above the ridge base. u0 is the mean horizontal wind velocity at the crest, oz is the standard deviation of vertical snow concentration (if the half cloud occupies the space between the plume axis and the terrain, we may write o_z z 0/2,15), Q_o is the source strength, narrow drift-flux at the crest (kg m⁻¹ s⁻¹), and is the gradient ratio of the stream function at the crest line to that at position x downwind; it may be approximated by =u₀/u_x. The principle and the notations may be verified in Figure 7(c).

The deposition of particles D at the snow surface is governed by the deposition velocity vd:

(10)

One usually assumes that the vertical distribution is unaffected by deposition and that the ground acts as a permeable surface and retains all material passing through it. The simplest approximation was to assume that the snow cloud or section of plume sinks with the particle fall velocity v_s, i.e. V_d = v_s. Since we know that the particles are deposited in turbulent wake flow, which is mainly governed by the shape of the terrain as a whole, we have chosen the deposition velocity at the ground surface as

(11)

which, for a hump-shaped ridge, amounts to

(12)

It is obvious that severe terrain features such as sharp crests or surface edges may not be described in this way, because differentiation is not possible for singular points.

Introducing now, as in the previous section in the case of potential flow, similar quantities for the terms of Equation (9) we may approximate the snow concentration at the ground surface and the deposition of snow with the aid of Equation (10) and Equation (12). For a comparison of model output deposition with observed total deposition as represented in Figures 1 to 4, we would have to run the model calculations at successive times with real source fluxes for ridge crests and meteorological parameters. Because such long-term data are not available, we confine the comparison to a correlation along the x-axis, i.e. we compare only the course of the deposition curve on Figure 7(a) with the combined deposition patterns on Figure 7(b) and (c). Figure 7(c) shows that the plume-model approach explains the first snow-depth maximum downwind of a ridge quite nicely, whereas the potential flow model seems to cause a flat second snow maximum towards the ridge-foot. By a combination of the two processes a zone of shallower snowpack may exist on steep lee slopes between the two snow maxima.

Figure 9 illustrates the combined effect of precipitation flux and surface drift-flux for the different ridge configurations previously represented in Figure 4. In order to simulate the extraordinary, concave shape of the second ridge profile in Figure 9, terrain function and, consequently, deposition velocity have been altered. According to Roffman and Grimble (1974), a damped sine wave has been used of the form:

(13)

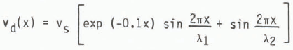
where λ₁ is 25 m, corresponding to the observed deposition wave length, and λ₂ is 250 m, corresponding to the ridge base length. According to these Figures it seems possible to simulate and to explain the main deposition features along simply shaped lee slopes, but not necessarily along more severe terrain configurations.

Fig. 9. Simulation of the observed pattern of snow deposition of Figure 4, theoretically approximated by a combination of potential flow and plume model results.

CONCLUSIONS

Elongated ridges oriented perpendicularly to the main wind direction show irregular snow deposits, mainly in a band of 20 to 50 m width on both sides of the crest line. The sharper the ridge is the narrower is the band width and the more distinct are the irregularities.

On lee slopes the snow-depth cross-profile may be viewed as a damped sine wave, whereby the amplitude is a function of ridge size and crest sharpness. On steep lee slopes (Ψ ~> 25°) the first snow-depth maximum downslope is attached to the crest line as a crest cornice. With decreasing crest sharpness this maximum moves gradually downslope. Lee slopes of mean slope angle are buried in midwinter under roughly twice as much snow as adjacent windward slopes. A medium-sized ridge system as a whole, like the ones surveyed, accumulates similar amounts of snow as comparable flat terrain.

The superposition of a surface-bounded snow plume and a potential flow of precipitation yields, for simply shaped, two-dimensional obstacles, a similar pattern of snow deposition to the ones observed in nature. However, for more complex terrain shapes, details such as, for example, the exact position and form of the crest cornice may not be approximated by these simple models. This is obvious, if we remember that particle distribution is non-uniform, often non-Gaussian, and that flow is fluctuating, showing reversed eddies as any typical wake flow does.