Introduction
Measuring ice-sheet surface elevation change using satellite and airborne altimetry is a valuable method for determining changes in the ice mass of both the Greenland and Antarctic ice sheets (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009; Reference ShepherdShepherd and others, 2012). In order to properly interpret the observed elevation change as mass change, however, the various processes that control surface elevation fluctuations must be considered. Outside of changes due to ice-flow dynamics, the ice-sheet surface may fluctuate in height due to variations in snow accumulation (used here interchangeably with surface mass balance (SMB) assuming it is always positive), firn compaction, basal melting and bed elevation (Reference Zwally and LiZwally and Li, 2002; Reference HelsenHelsen and others, 2008; Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011; Reference GunterGunter and others, 2014). Measuring these variations at a scale comparable to the observed altimetry changes (i.e. ice-sheet-wide) is essentially impossible, so models are typically used (Reference ShepherdShepherd and others, 2012).
The changes in surface elevation due to SMB variability have recently been accounted for using a regional climate model (Reference Pritchard, Ligtenberg, Fricker, Vaughan, Van de and PadmanPritchard and others, 2012; Reference ShepherdShepherd and others, 2012) or global reanalysis precipitation-minus-evaporation product (Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006). Firn compaction changes have similarly been simulated using SMB and temperature forcing from a climate model (Reference Pritchard, Ligtenberg, Fricker, Vaughan, Van de and PadmanPritchard and others, 2012). While spatio-temporal measurements of SMB are difficult and few, measurements of firn compaction are even rarer. For example, Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010) measured vertical strain in the firn at hourly intervals over several years at three sites in Antarctica to investigate the controls on compaction rates as well as to evaluate different firn densification models. In Greenland, tracking the displacements of features observed using borehole optical stratigraphy over a single year at Summit provided measurements of the vertical compaction profile of the firn (Reference Hawley and WaddingtonHawley and Waddington, 2011). Finally, repeat measurements of the firn density profile, derived using a neutron-scattering technique, along a ~500 km traverse allowed Reference Morris and WinghamMorris and Wingham (2011, Reference Morris and Wingham2014) to measure strain rates as a function of depth and develop a new densification equation based on their findings. The models developed by the aforementioned studies are tuned by data ranging from a few data points (Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others, 2010) to a few tens of sites (Reference Morris and WinghamMorris and Wingham, 2014), which limits their use outside of the surveyed areas. Thus, some ground-truthing of the temporal and spatial variability of compaction rates derived from firn densification models exists, but their evaluation would benefit from a method that can easily measure compaction rates over large areas. Additionally, steady-state firn densification models are often tuned by point measurements of the density profile (e.g. Reference Herron and LangwayHerron and Langway, 1980; Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011) and thus do not incorporate any transient information such as actual rates of compaction.
One method to measure firn compaction remotely is with an instrument that can image subsurface horizons at an initial point in time t 1 and again at a later point t 2 (e.g. Reference Hawley, Waddington, Lamorey and TaylorHawley and others, 2004). The thickness change (m) between the marker and the t 1 surface divided by the time interval (i.e. t 2 – t 1) yields the firn compaction rate (m a−1). Both ground and airborne radar systems image the internal stratigraphy in the firn column; however, few studies have used these natural markers to determine firn compaction rates (Reference Kruetzmann, Rack, McDonald and GeorgeKruetzmann and others, 2011; Reference Simonsen, Stenseng, Aðalgeirsdóttir, Fausto, Hvidberg and Lucas-PicherySimonsen and others, 2013). Recent work by Reference MedleyMedley and others (2013) highlighted the potential of imaging the internal stratigraphy of the firn column from airborne radar data for determination of the spatio-temporal variability in SMB and produced a dataset with which to test various SMB model outputs at the basin scale. Here we use the same airborne radar data collected as part of NASA’s Operation IceBridge (OIB) mission over the Thwaites Glacier catchment, West Antarctica, to investigate its use in calculating firn compaction rates over several repeat tracks from three time intervals (2009–10, 2010–11 and 2009–11). Specifically we discuss: (1) the radar data and firn compaction measurements, (2) the strengths and limitations of using radar to measure compaction, (3) the spatial and, to a lesser extent, temporal compaction variability, and (4) potential improvements to this study.
Snow Compaction Measurements
In this section, we briefly discuss the radar system and describe the methods used to convert between radar two-way travel time and depth and to estimate the firn compaction rate. Discussion of the potential uncertainties in our measurements and a description of the estimated errors in our depth measurements are provided in the Appendix.
Radar data
For this work, we used data collected by the Center for Remote Sensing of Ice Sheets (CReSIS) ultra-wideband microwave radar system, hereinafter referred to as the ‘snow radar’, which was flown on NASA’s OIB mission. The radar surveys were collected on 18 October 2009, 19 November 2010, and 9 and 12 November 2011 (Fig. 1). The frequency-modulated, continuous-wave snow radar operated over frequency ranges of 4–6 GHz in 2009 and 2–6.5 GHz in 2010 and 2011 and has a range resolution in firn (ρ = 0.55 g cm−3) of 9 cm and 4 cm for the 2009 and 2010–11 surveys, respectively. Complete descriptions of the radar system and its performance as well as the field deployments are provided by Reference PanzerPanzer and others (2013) and Reference Rodriguez-MoralesRodriguez-Morales and others (2013). The radar reflection horizons represent contrasts in the material’s dielectric permittivity, likely due to isochronous buried sequences of hoar layers and associated ice crusts (Reference Arcone, Spikes, Hamilton and MayewskiArcone and others, 2004, Reference Arcone, Spikes and Hamilton2005a,Reference Arcone, Spikes and Hamiltonb; Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004). An earlier study by Reference MedleyMedley and others (2013) found the radar system capable of resolving near-surface (<50 m), annually spaced horizons over much of the Thwaites Glacier catchment area. Here we use the manual horizon picks from that study to measure firn compaction rates between the different survey years where repeat-track measurements exist (Fig. 1).

Fig. 1. Location of the repeat-track airborne snow radar surveys used in this study, colored by the time interval of repeat measurements. The base map is the Moderate Resolution Imaging Spectroradiometer (MODIS) Mosaic of Antarctica (Reference Scambos, Haran, Fahnestock, Painter and BohlanderScambos and others, 2007) overlaid by the ice-surface velocity (Reference JoughinJoughin, 2002). The black lines represent 200 m surface elevation contours, with every 1000 m bolded. The different survey lines are referred to in the text by their representative letter (A–D), and the white line delineates the catchment boundaries. The inset map of Antarctica shows the location of the regional-scale map.
After stacking radar traces, the approximate along-track resolution is ~25 m for 2009 and 2010, and ~50 m for the 2011 survey. A more rigorous approach could have varied the stacking procedure to obtain similar measurement spacing. Because the radar horizons were already tracked in a previous study (Reference MedleyMedley and others, 2013), we did not reprocess the radar data in order to eliminate the need to digitize the horizons for a second time. Therefore, we simply compare the thickness measurements between the closest stacked traces from the two echograms, while limiting the analysis to traces that are <20 m apart, a value close to the radar footprint (Reference PanzerPanzer and others, 2013).
Methodology
To measure firn compaction, we determine the change in thickness between two tracked horizons at two points in time for a given location. We define compaction as positive in sign (i.e. a thickness decrease), and it is determined by subtracting the t 2 thickness from the initial t 1 thickness and dividing by the time interval between measurements, resulting in a rate of change (m a−1). We estimate the cumulative compaction (i.e. compaction relative to the original surface) to several dated horizons as well as the compaction between adjacent horizons (i.e. a depth-varying compaction rate). Specifically, we use the 2005, 2000, 1995, 1990, 1985 and 1980 horizons (Fig. 2) to determine compaction rates over the repeat surveys (A–D) shown in Figure 1. We also track the 2009 surface (here labelled as ‘2010’ since the survey took place in the late fall of 2009) in the 2010 and 2011 echograms and the 2010 surface (labelled as ‘2011’) in the 2011 echogram, which allows us to determine the amount of snow that accumulated between the radar surveys and provides the upper horizon with which the cumulative compaction rates are estimated. The horizons are dated using their annual stratigraphy, which was confirmed in Reference MedleyMedley and others (2013). A previous study by Reference Kruetzmann, Rack, McDonald and GeorgeKruetzmann and others (2011) used a ground-based radar system to estimate compaction rates to depths of <15 m on the McMurdo Ice Shelf. Here we use a similar method to test the feasibility of using an airborne radar system that is capable of imaging deeper horizons in the firn column over much greater distances.

Fig. 2. Sample snow radar echograms covering the same 26 km stretch and collected 2 years apart. This area was initially sampled on 18 October 2009 (left) and again on 12 November 2011 (right). The manually digitized horizons used in this study are delineated in red, and their ages are listed adjacently in boxes, which were confirmed by comparison between the radar-derived depth–age scale and a firn core depth–age scale at their intersection. Note that the radar system operated over different frequency ranges in these surveys, resulting in coarser vertical resolution in 2009 than in 2011.
To determine the depth to each of the horizons we use the formula d = 0.5cτ∊−0.5 for conversion between twoway travel time τ and depth d, where c is the wave speed in a vacuum and ∊ is the dielectric permittivity. Because ∊ is density-dependent and the density profile varies in time and space with accumulation and temperature, it is difficult to prescribe the appropriate dielectric permittivity over the entire survey region. The accumulation rate varies substantially over small distances in this region: specifically, by up to 12% within a 6 km distance (Reference MedleyMedley and others, 2013, Reference Medley2014). Therefore, the limited sampling by firn-core density measurements cannot resolve the density profile variability resulting from the climate variability of the region. Previous studies have interpolated the density profile between two firn cores (e.g. Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004), thereby presuming that the dominant variation is linear and that the cores represent the average conditions at either end (i.e. are not biased substantially in an area of higher/lower accumulation). Because accumulation is highly variable over short distances, both the former and latter inherent assumptions are challenged, and thus, we have developed a new method that generates spatially varying density profiles that are0 consistent with the radar-derived accumulation rates.
The horizon depths observed in the radar echograms contain information on the accumulation rate and densification rate, the dominant controls at these limited depths. To generate a consistent accumulation rate and steady-state density profile at a given location, we begin with the Reference Herron and LangwayHerron and Langway (1980) densification model and an initial accumulation rate estimate to generate a steady-state density profile (Fig. 3). Using this profile, we next calculate the dielectric permittivity profile using a mixture model (Reference LooyengaLooyenga, 1965) for ice and air and ultimately the depth to each horizon using the formula described above and in Figure 3. A cumulative mass profile, generated by integrating the modeled density profile with depth, provides the total mass per unit area above a given depth. Dividing the cumulative mass above the oldest horizon by the horizon age (2009: 30 years; 2010: 31 years; 2011: 32 years) provides the long-term average accumulation rate (m w.e. a−1). This new accumulation rate is fed back into the Reference Herron and LangwayHerron and Langway (1980) densification model, and the entire process repeats itself until it converges on a long-term accumulation rate and steady-state density profile that are consistent with the radar measurements and the densification model. From a regional perspective, the variations in temperature and surface density are included in the densification model through incorporation of the 1979–2012 average surface temperature and surface density from a regional atmospheric climate model (RACMO2; Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012). Therefore, the RACMO2 average temperature and surface density are simply inputs into the densification model, and they vary spatially but are not allowed to evolve like the accumulation rate. As a result, the compaction rates presented are partly dependent on the long-term climate from the RACMO2 climate model. Specifically, the RACMO2 27 km gridded surface density and temperature were bilinearly interpolated to each radar point measurement, assuming variations of these products are not substantial over shorter distances. The RACMO2 1979–2012 mean accumulation rate was used as the initial accumulation estimate, which did not ultimately impact the results. The entire process is outlined in Figure 3.

Fig. 3. Flow chart depicting the method for calculating a steady-state density profile that is consistent with the radar-derived accumulation rates at a given location. The variables displayed are as follows: d and τ are depth and radar two-way travel time, ![]() and
and ![]() are the 1979–2012 average annual temperature and surface density from RACMO2, A is the long-term accumulation rate, A
0 is an initial accumulation rate guess, ρd
, ∊d
and CM
d
are the depth-dependent density, dielectric permittivity and cumulative mass profiles, c is wave speed in a vacuum,
are the 1979–2012 average annual temperature and surface density from RACMO2, A is the long-term accumulation rate, A
0 is an initial accumulation rate guess, ρd
, ∊d
and CM
d
are the depth-dependent density, dielectric permittivity and cumulative mass profiles, c is wave speed in a vacuum, ![]() is the average dielectric permittivity above a given depth, τa
and da
are the two-way travel times and depths to a horizon of a given age a, A
80 and CM80 are the average accumulation rate and cumulative mass above the 1980 horizon, Δt is the age interval (for the 2009 survey: 30 years; 2010: 31 years; 2011: 32 years) and ρw is the density of water.
is the average dielectric permittivity above a given depth, τa
and da
are the two-way travel times and depths to a horizon of a given age a, A
80 and CM80 are the average accumulation rate and cumulative mass above the 1980 horizon, Δt is the age interval (for the 2009 survey: 30 years; 2010: 31 years; 2011: 32 years) and ρw is the density of water.
This method allows us to calculate different density profiles based on the variable climate conditions over these flights. All of the profiles are generated in such a way, and the average climate conditions and resulting density profile are shown in Figure 4a. Comparison between modeled and measured density profiles at six locations reveals a root-mean-square error (RMSE) of 0.022 g cm−3, with values ranging between 0.015 and 0.026 g cm−3. These results indicate that the RMSE is <5% for depths below ~5 m. The conversion between depth and two-way travel time is then uniquely calculated for each location based on the estimated density profile. Compaction rates are then measured by determining the layer thicknesses at each location, and determining their change from one survey to the next. A complete description of the measurement uncertainty is detailed in the Appendix. The uncertainty in depth and its components for the regional average density profile are shown in Figure 4b.
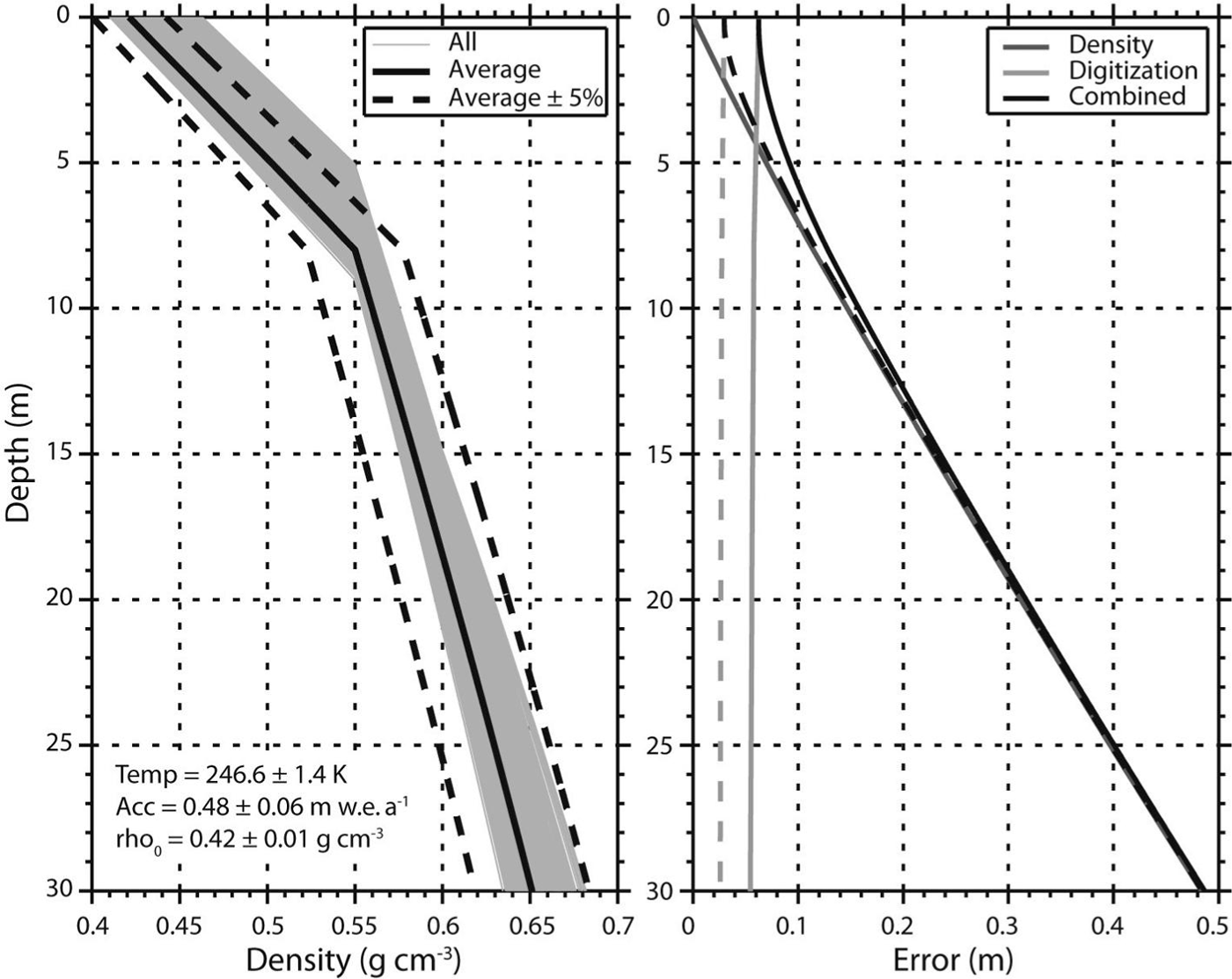
Fig. 4. Density profiles and average depth errors and their components. (a) All estimated density profiles determined using the method outline in Figure 3 over the flight segments in Figure 1 are plotted in gray. The solid black line shows the average profile, and the dashed black lines are ±5% of the average. The climate parameters associated with the average (±1 σ) profile from this region are also listed. (b) The error in the depth determination of the radar-mapped horizons from the average density profile shown in (a). The digitization error is shown in light gray, and the error generated from the ±5% error to the average is in gray. Their combination is in black. The solid (dashed) lines show the errors for the 2009 (2010–11) radar survey.
Results
The paths in Figure 1 show the locations of the flight surveys where repeat measurements exist and radar horizons have already been tracked by Reference MedleyMedley and others (2013). While we were able to measure compaction for the 2009–10 and 2010–11 intervals, the majority of the measurements cover the 2009–11 period simply due to the fact that the largest overlap exists between those surveys. In total, our measurements cover >500 km of flight surveys within the Thwaites Glacier catchment.
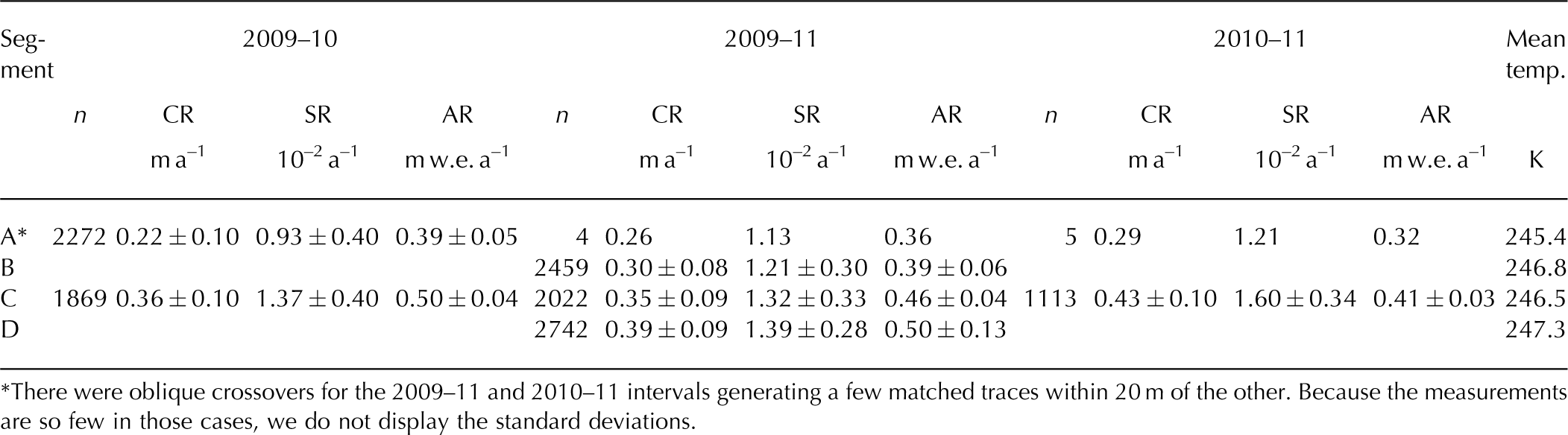
The average compaction and strain rates to the 1980 horizon and the interval accumulation rate for all segments and time intervals are shown in Table 1. The largest average compaction rate of 0.43 ± 0.10 m a−1 is found along the C transect over the 2010–11 interval, while the A segment over the 2009–10 interval had the lowest average of 0.22 ± 0.10 m a−1. There is coverage over all the segments during the 2009–11 interval, which allows for investigation into the spatial variations in the compaction rate. The comparison indicates enhanced compaction rates are found in areas of higher accumulation rates for each individual interval (Table 1). We consider the differences in compaction rates over the C segment to investigate the temporal variability, where both the 2009–10 and 2010–11 intervals were measured. Here there is a divergence from the compaction- and strain-rate (i.e. depth-normalized compaction rate) dependence on the accumulation rate: we find more snow accumulated but less compaction occurred in 2009–10 than in 2010–11.
Table 1. The spatial average and standard deviation of the compaction rates (CR), strain rates (SR) and accumulation rates (AR) and number of traces (n) for each segment and time interval, and the mean temperature from RACMO2
In Figure 5, the accumulation rate and cumulative compaction rate to the oldest horizon (1980) between 2009 and 2011 are shown along the B segment (see Fig. 1). While we only show a single segment, all of the segments indicate a direct relationship between the accumulation rate and compaction rate where locations with higher than average compaction rates typically incur larger accumulations. Comparisons with strain rates show a nearly identical pattern. Table 2 shows the correlations between the accumulation rate over the survey interval as well as the 30 year average and cumulative strain rates to the 2005 and 1980 intervals. In all cases, the interval, rather than the 30 year average, accumulation rates are more strongly correlated spatially with the interval strain rates. None of the compaction rates estimated over depth intervals below the 2005 horizon are significantly correlated with the accumulation rate and they are not displayed.
Table 2. Correlation coefficients relating the interval and 30 year accumulation rates and the strain rates to the 2005 and 1980 age horizons for each interval. All p-values, listed in parentheses, account for autocorrelation

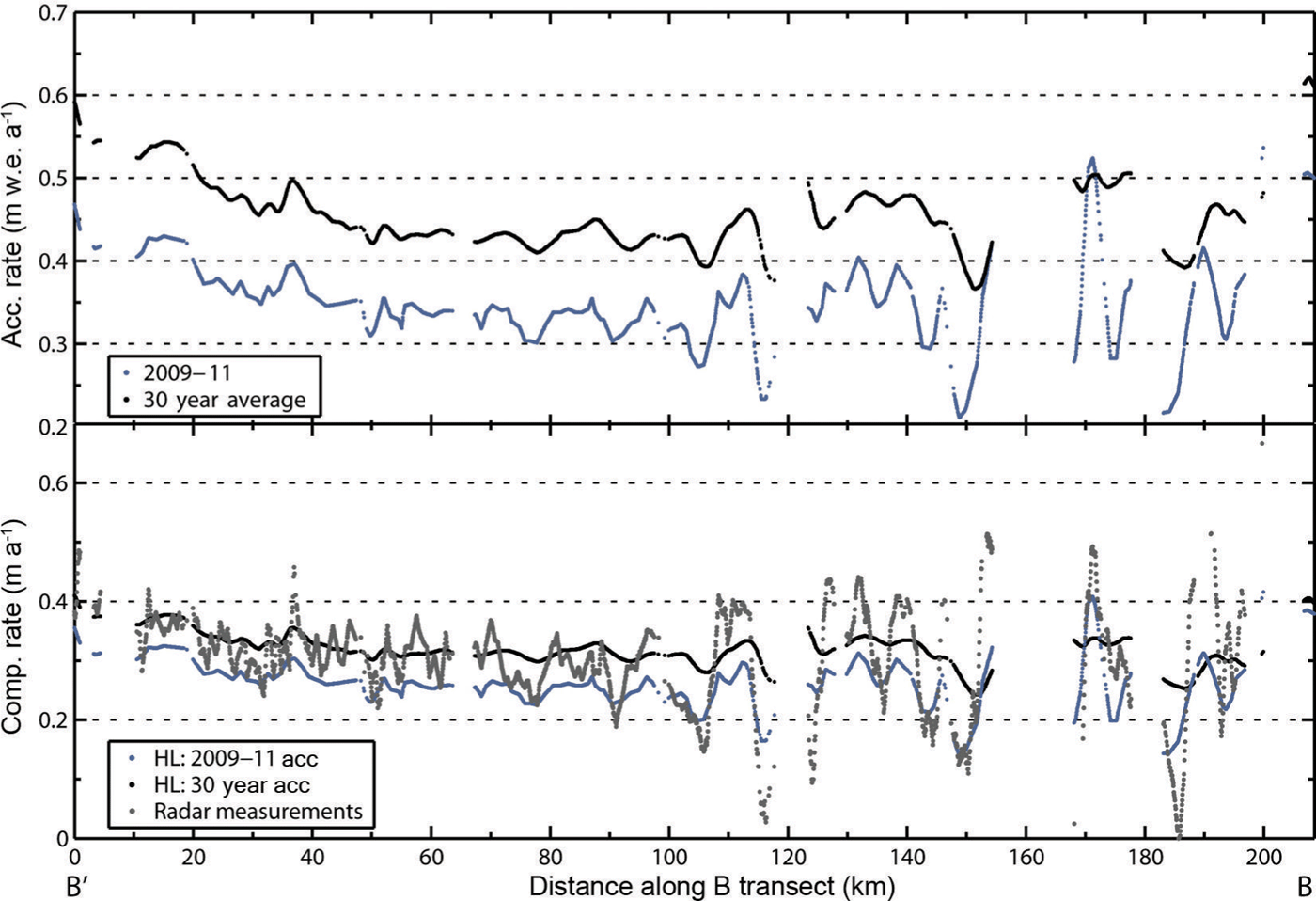
Fig. 5. The accumulation and compaction rate variability along the B segment (see Fig. 1), representing the average rates between the 2009 and 2011 surveys. The top plot shows accumulation rates for the survey period (2009–11: blue) and the long-term average (30 year average: black). The bottom plot shows the measured and modeled compaction rates over the same transect, where the modeled rates are estimated for the same intervals as the measurements (30 years of firn over a 2 year interval) using the Reference Herron and LangwayHerron and Langway (1980) densification model. Specifically, the radar-derived compaction rates are shown in gray, the modeled rates using the survey period accumulation rate are in blue and those using the long-term average are in black. The correlation coefficient between the radar compaction rate measurements and the 2009–11 accumulation rates is 0.78 (p < 0.01), indicating that 60% of the spatial variations in compaction rates can be explained by the accumulation rate.
Figure 5 also suggests that the compaction measurements are more variable spatially than the accumulation rates, which could be caused by a few factors. First, the compaction rates are based on two picks of the same time horizon whereas the accumulation rate is determined by a single pick, which means the noise will be greater in the former. Second, the horizon depth variations due to the variable accumulation rates are significantly steepened with depth when the surface return is zeroed (see Fig. 2). Because the compaction and accumulation rates are based on the 1980 and 2009 horizons respectively, the spatial variations in depth to the 1980 horizon are more precisely determined than the 2009 horizon. Thus, spatial variations in the compaction rate are more precisely determined than variations in the accumulation rate.
The measured compaction rates along the B transect are compared to model estimates of the compaction rate using the Reference Herron and LangwayHerron and Langway (1980) densification model (Fig. 5). To ensure consistency between the model and measurements, we modeled the compaction rates of 30 year firn over a 2 year interval. Compaction rates were then estimated using the interval (2009–11) accumulation rate as well as the 30 year average accumulation rate. For the most part, the measured compaction rates fall between those modeled using the 30 year and interval accumulation rates. While the model and measurements compare well, the modeled compaction rates do not replicate all variations observed in the compaction rate measurements. This disagreement is likely the result of one or more of the following: (1) the precision of accumulation measurements was not sufficient to match the compaction measurements since the thickness of the accumulation layer is much less than the thickness to the 1980 horizon, (2) the compaction measurements are noisier due to additional horizon picking (see previous paragraph), (3) the dependence of the densification rate on accumulation is not adequately accounted for in the Reference Herron and LangwayHerron and Langway (1980) model, (4) or small-scale variations in temperature or the surface density are not included.
Cumulative compaction profiles from the different time intervals, binned according to their interval accumulation rate, are shown in Figure 6. For all intervals, the largest compaction rates occur in the youngest firn near the surface (to the 2005 horizon). As older firn is included, the cumulative compaction rate increases at a decreasing rate. Evaluation of the impact of accumulation on the cumulative compaction rate profile indicates higher (lower) accumulation results in enhanced (reduced) compaction rates on average, without consideration of the variations in temperature. Finally, comparing the profiles from different time intervals, we find that the total cumulative compaction varies between the three time intervals when considering locations of similar accumulation. Specifically, the 2010–11 compaction rates are greater than the 2009–10 rates under the same interval accumulation rate.
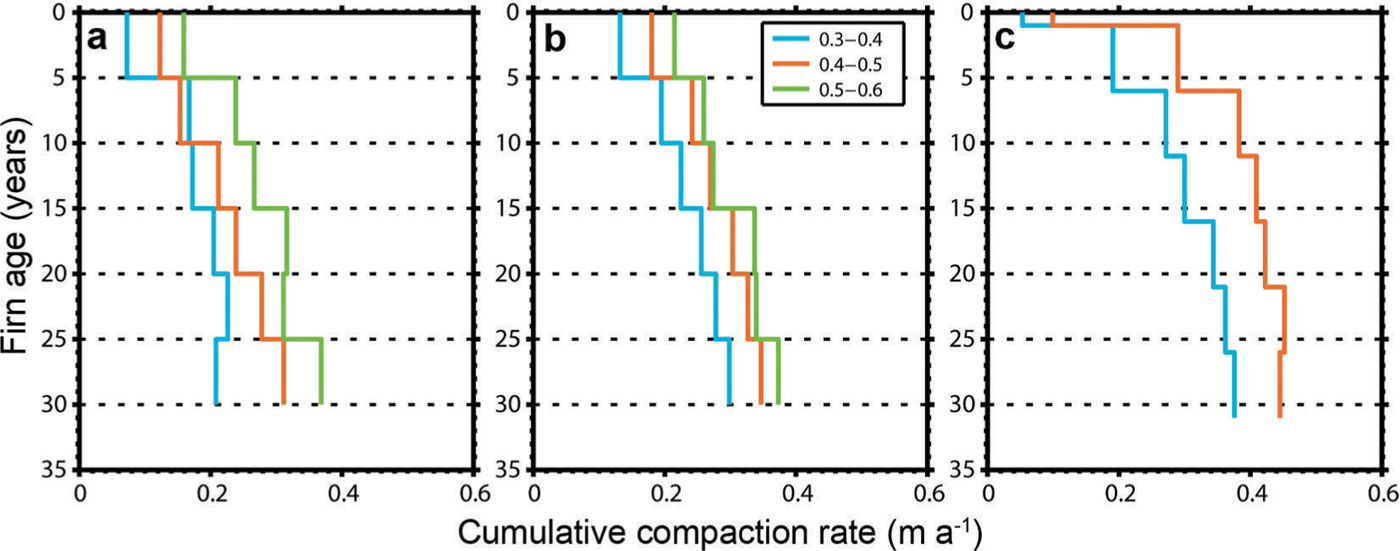
Fig. 6. Comparison of measured cumulative compaction rate (between a given age horizon and the surface) profiles for (a) 2009–10, (b) 2009–11 and (c) 2010–11 relative to constant age horizons. Multiple plots on a given graph represent the average profiles over the accumulation rates (m w.e. a−1) listed in the legend. No measurements of compaction rates where the accumulation rate is >0.5 m w.e. a–1 exist for the 2010–11 interval.
Discussion
Our results indicate that repeat airborne radar surveys provide the measurements necessary to estimate the firn compaction rate and its variability at the regional scale. Therefore, the potential exists to not only measure surface elevation fluctuations but also coincidently capture the spatio-temporal variations in the firn densification process to aid in interpretations of elevation change. We find that our compaction rate measurements fall within the range of those expected from a simple densification model (Fig. 5), and are comparable to other published values. For comparison, the compaction rate to 20 m depth at a site on Berkner Island, where the accumulation rate is about a quarter of the average in this region and the temperature is similar, was 0.21 m a−1 (Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others, 2010). The same study found compaction rates of 0.54 m a−1 on Dyer Plateau, where the accumulation rate is 50% larger and the temperature is ~5K higher than the average in our study area. The regional averages (Table 1) fall between these two values, as expected based on the relative climate conditions of the different regions.
Strengths and limitations
The ability to measure compaction rates remotely over hundreds of kilometers makes this method extremely valuable. While the depths to various markers have previously been measured in situ, these methods require considerable fieldwork, which limits the spatial coverage of measurements. By measuring depths to various horizons, radar-derived compaction rate measurements do not have to compromise spatial coverage for spatial resolution and vice versa. Furthermore, measuring bulk or depth-varying compaction rates is possible through measurement of a single or multiple depth horizons. The method presented also eliminates the need for in situ density measurements in the conversion between radar two-way travel time and depth in the dry-snow zone by iteratively converging on a density profile consistent with the radar-measured accumulation rates. Finally, the use of OIB radar data allows for simultaneous and co-located measurements of accumulation and firn compaction rates and surface elevation change from the OIB Airborne Topographic Mapper (ATM) dataset, which will allow for precise segmentation of the observed elevation change into near-surface and dynamic components.
Certain limitations exist as well. Compaction rates are on the order of tens of cm a−1, and the radar range resolution, especially from 2009, is approximately the same order of magnitude. This resolution issue limits the measurement precision, especially when measuring compaction rates over a single year; however, the radar resolution was substantially improved in 2010. Tracking the horizons manually is time-consuming and potentially subjective, but we note the stratigraphy (i.e. horizon pattern) in this region is for the most part unambiguous (see Fig. 2), improving our ability to identify the same horizon in multiple surveys. Unless horizon misidentification resulted in non-physical expansion, it is difficult to determine where misidentification occurred and could result in false compaction results. Furthermore, this work shows that firn compaction rates vary from one year to the next, yet we use a steady-state density profile to ultimately determine horizon depths. While we ignore temporal variations in the density profile, because we are only looking at a 2 year interval and multi-year firn layers, their impact on depth determination is minimized. Finally, rather than measuring compaction rates to a horizon of constant depth as is usual, this method calculates rates to a horizon of constant age. While this difference is not necessarily a limitation, consideration of the impact on our results and their interpretation is warranted and discussed in the Appendix.
Spatial variability
Firn compaction rates are climate-controlled and are therefore expected to vary spatially with the surface climate. The accumulation rate varies substantially in this region (Fig. 5) and, as a result, compaction rates vary as well. Spatial variations in surface temperatures will generate variations in firn compaction rates; temperature measurements of comparable spatial resolution, however, do not exist, which complicates determination of the dominant control (temperature or accumulation) on compaction rates. Considering the 2009–11 interval, we find that compaction and strain rates increase on average starting at segment A and moving towards D. This increase is accompanied by an increase in the accumulation rate (Table 1). The temperature does generally increase, but the B and C segments are nearly equal. Therefore, spatial variations in temperature likely generate changes in the compaction rates, but in this region where temperatures do not differ greatly, they might play a secondary role to spatial variations in the accumulation rate. Additional temperature data of comparable spatial resolution would allow for better interpretation of the temperature relationship. Furthermore, if the analysis included a much greater range of climate conditions, the importance of spatial variations in the temperature would likely be more apparent. At the local scale, variations in the compaction and strain rates are strongly correlated with the interval accumulation rate (r > 0.5; Table 2). We find that local variations in the compaction rate are partly controlled by the accumulation rate, but the lack of similar-resolution temperature data means we cannot fully determine its role at the local scale. At the regional scale, both accumulation and temperature, not surprisingly, are controls on the spatial variations in the compaction rate. In general, our compaction rate measurements show the expected positive relationship with both temperature and accumulation.
Temporal variability
While the spatial variations in cumulative compaction rates indicate a positive relationship with accumulation, the temporal dependence of the depth-variable compaction rate on the accumulation rate is less obvious (Fig. 6). The C segment experienced greater accumulation rates in 2009–10 than in 2010–11, but smaller compaction rates. Also, Figure 6 indicates that the compaction rates are larger under the same accumulation regime in 2010–11 than in 2009–10, especially closest to the surface. Therefore, our results indicate that, for a given accumulation rate, more compaction occurred in the 2010–11 interval than in the 2009–10 interval. While the exact reason for this discrepancy is unknown, we offer a few possibilities.
First, our 2010–11 average compaction rates could be larger than the 2009–10 rates if the 2010–11 measurements were taken from an area of higher surface temperatures and, thus, enhanced compaction. At the locations where we were able to calculate compaction for both time intervals along segment C, however, we found greater accumulation in 2009–10 but lower rates of compaction, indicating our sampling difference between intervals is likely not the cause (Table 1). Second, the 2010–11 interval could have potentially been warmer than the 2009–10 interval, speeding up the rate of compaction. This explanation is reasonable, but the temperature record from RACMO2 indicates that the 2009–10 and 2010–11 intervals experienced nearly identical annual temperatures (see Reference Ligtenberg, Medley, Van den Broeke and Kuipers MunnekeLigtenberg and others, 2015). Third, the 2009 survey was collected about a month earlier in the year than the 2010 survey. This difference means that the winter accumulation in 2009 might not have undergone as much compaction as in 2010 since it was collected in October, missing an additional month of higher temperatures and compaction. While this difference could result in overestimated accumulation rates for 2009–10 relative to 2010–11, because most compaction occurs in the summer (December–February), it is likely not a significant contributor to the accumulation difference.
Finally, the seasonality of accumulation could play a role, which we surmise is the most likely possibility. The majority of accumulation in this sector of West Antarctica occurs in the winter and spring (Reference Nicolas and BromwichNicolas and Bromwich, 2011), which falls just before the survey dates. Therefore, if indeed there was additional accumulation over the 2009–10 interval, the majority of it likely fell just before the radar data were collected in 2010, affecting the 2010–11 compaction rates more than the 2009–10 rates. Specifically, the presence of a thick, low-density snow layer near the surface could produce the larger compaction rates observed. Radar and firn-core (Reference MedleyMedley and others, 2013) and RACMO2 (Reference Ligtenberg, Medley, Van den Broeke and Kuipers MunnekeLigtenberg and others, 2015) records of annual accumulation show that accumulation was lower in 2009 than in 2010. Therefore, we believe that the lower compaction rates in the 2009–10 interval are due to a thinner and thus lighter accumulation of new snow likely deposited just before the 2009 survey. As a result, there was (1) less low-density snow to compact and (2) less overburden pressure to compact the underlying snow during the 2009–10 interval. Assuming the snow deposited from year to year is approximately the same, when a thicker snow layer was deposited before the 2010 survey, a thicker amount of low-density firn is available for compaction. A longer interval of consideration (3–5 years) would allow us to better evaluate this hypothesis. Thus, we find accumulation differences prior to the radar surveys are the most likely reason, but also acknowledge that there are many reasons (some of which we have discussed) that could potentially cause the difference in compaction rates from year to year. Our hypothesis suggests the temporal variability in accumulation impacts the variability in compaction; however, the impact of the temporal variability in temperature cannot be determined, as the mean temperatures over both time intervals were nearly identical. Therefore, it is important that temporal variations in the accumulation rate are accounted for when modeling compaction rates.
Future study improvements
While we find that the method and results presented are reliable, many potential improvements could be made. This work used data collected between 2009 and 2011, but the radar data collected since 2010 have the finest vertical resolution, so future studies should focus on the higher-quality data. Along similar lines, OIB to this point has collected radar data over 6 years (2009–14), which means that future studies can investigate compaction rates over longer time intervals, providing higher-quality compaction rate measurements. The work would greatly benefit from implementation of an automated horizon-picking scheme, which not only would save time but also would provide objective horizon picks. The method presented could be further improved by implementing a transient densification model, but considering we are measuring multi-year firn, this might not provide substantial improvement overall. The study design could be improved by selecting more appropriate horizons to measure: compaction is greatest near the surface and rapidly decays with depth and, as a result, more horizons should be measured near the surface and fewer at depth. Thus, measuring compaction within a thicker firn layer (i.e. age intervals >5 years), especially deeper in the firn column, would produce more precise results. Finally, measurements over a larger range of temperatures would provide better insight into controls on the spatio-temporal variability in the compaction rate.
Conclusion
By providing depth measurements to horizons of constant age, the CReSIS snow radar delivers the data necessary to remotely measure firn compaction rates where repeat surveys with identifiable annual horizons exist. Because the CReSIS radar is flown as part of NASA’s OIB mission, a unique opportunity now exists where the data required to measure accumulation and firn compaction rates such as those presented here are collected simultaneously with the change in surface elevation. Compaction rates were estimated along hundreds of kilometers of the flight paths. Locations where the repeat horizon is incorrectly identified show non-physical expansion of the firn column; these non-physical results, however, make up only a small portion of the measurements and were largely eliminated through robust regression analysis (see Appendix). The measurements indicate that the spatial variations in the compaction and strain rates are partly controlled by the accumulation rate at the local and regional scale. The influence of spatial variations in temperature is less clear, but at the regional scale higher temperatures are associated with larger compaction rates. Interestingly, the 2009–10 average accumulation rate was larger and the compaction rate was smaller than in 2010–11. Because the majority of the accumulation in this region typically occurs in the month(s) prior to the survey dates (Reference Nicolas and BromwichNicolas and Bromwich, 2011), we surmise the enhanced 2009–10 accumulation likely affected the 2010–11 compaction rates more than the 2009–10 rates.
Our results indicate that accumulation rates, and thus compaction rates, vary substantially in space and time. As a result, measuring surface elevation change, the accumulation rate and firn compaction rate simultaneously would improve the precision in determining mass change from elevation change. Using the OIB snow radar and ATM data over the dry-snow zone, in conjunction with a densification model as presented here, it is now possible to measure the surface elevation change due to surface processes and total surface elevation change at the same time and location, providing a precise determination of mass change from volume change. The potential exists for investigating compaction over different climate regimes since several repeat OIB surveys exist over the Greenland ice sheet and future repeat surveys are possible over both Greenland and Antarctica.
Acknowledgements
We thank C. Miège and an anonymous reviewer for constructive comments. B. Medley was supported by an appointment to the NASA Postdoctoral Program at the Goddard Space Flight Center, administered by Oak Ridge Associated Universities through a contract with NASA. The research at the University of Washington (I. Joughin, B. Medley) was supported by US National Science Foundation (NSF) Office of Polar Programs (OPP) grants ANT-0631973 and ANT-0424589. S.R.M. Ligtenberg and M.R. van den Broeke acknowledge support from Utrecht University and the Netherlands Polar Programme of the Earth and Life Sciences division of the Netherlands Organization for Scientific Research (ALW/NWO). S. Nowicki acknowledges support from the NASA Cryospheric Sciences Program. Radar development, data collection and processing are partially supported by NSF OPP grant ANT-0424589 and NASA under grants NNX09AR77G, NNG10HP19C and NNX10AT68G. We also acknowledge the generous contribution of faculty, staff and students at CReSIS in collecting and processing the data. Most of the data used in this work were acquired by NASA’s Operation IceBridge Project.
Appendix
Error estimation
The error in horizon depth depends on the uncertainty introduced in the conversion between d and τ which originates from the uncertainty in the density profile as well as the digitization error of the radar horizons. Here we assign a ±5% error to the estimated density profiles and a ±1 range bin digitization error (2009: 5.8 cm and 2010/11: 2.7 cm at a density of 0.55 g cm−3). Their respective contributions to depth error are displayed in Figure 4b for the average density profile estimated over the surveyed area (Fig. 4a). Error estimates vary spatially, due to the use of spatially varying density profiles, and by survey year, due to different radar system properties. Because any error in the density profile results in a depth-cumulative error (i.e. the error increases with depth), this component dominates depth errors except in the upper 5 m of the firn column (Fig. 4b). While a density error of 5% is reasonable based on the RMSE of modeled versus measured density profiles, we note that the bounds incorporated by this error for the average density profile (Fig. 4a) exceed the actual bounds of all the estimated density profiles, suggesting this assigned error potentially overestimates the actual error, especially at depths below 10 m. Positional errors can also generate errors in our compaction measurements, especially considering we allow comparison between measurements up to 20 m apart. We do not directly account for positional error, but note that this error could be substantial in areas with extreme gradients in accumulation.
While we do not consider the temporal variability in the density profile, because collection of the radar data occurred at the same time of the year (they were all collected within a 1 month window), the impact of any intra-annual variations is minimized (Reference Morris and WinghamMorris and Wingham, 2014). At the same time, the densification rate and thus density profile will vary between survey years; use of a steady-state density profile to measure horizon depths is adequate, however, because we are evaluating changes to multi-year firn. Finally, it is important to consider the time interval over which the measurements were taken, which in our study is either 1 or 2 years. The longer the time interval between measurements, the larger the total compaction, which means the changes are more easily resolved. Therefore, the compaction estimates between 2009 and 2011 are the most precise.
Another potential source of uncertainty is our assumption that we have correctly determined the annual stratigraphy in each survey and are thus comparing horizons of the same age. Any misidentification of annual layers could result in largely incorrect and unphysical results (i.e. negative compaction rates or expansion). To remove any of these potential outliers, we determined a robust linear fit between the radar-measured accumulation and compaction rates for each of the survey periods, and we removed points that had residuals greater than three times the standard deviation. This process removes extreme outliers, such as those derived by horizon misidentification; however, only 2% of the data points were excluded, suggesting horizon picks were mostly valid. Errors assigned to individual points can be large, but averaging the measurements substantially reduces the noise; therefore, the standard deviation (see Table 1) provides a good metric for the spatial variability in firn compaction rates.
Age versus depth horizons
One important consideration is whether surveying horizons of constant age, rather than depth, will complicate the comparison of measured compaction rates for different accumulation rates. Specifically, surveying to a constant age horizon implies that the depths and thicknesses considered vary based on the accumulation rate: in areas of high accumulation, the depth of a given age horizon will be much greater than in lower-accumulation areas, and the thicknesses considered are greater. As a result, the areas of high accumulation will have additional dependence on the accumulation rate outside of the influence on the densification rate. At the same time, consideration of the depth-normalized compaction rates (i.e. strain rates) should have the opposite effect: strain rates will be biased high for low-accumulation sites because the survey is shallower, encompassing the region of enhanced compaction rates. Even when the strain rates are biased high (low) in low (high-)accumulation areas, a strong relationship between accumulation and the strain rates is observed (Table 2). Correlation of the interval accumulation and compaction rates, rather than strain rates, shows the enhanced dependence (r = 0.63–0.78): for each time interval, the coefficient increased relative to the coefficient estimated between accumulation and strain rate. Interestingly, the correlation between strain rates and the 30 year average accumulation rate is greatly reduced relative to the correlation with the interval accumulation rate (Table 2). These results suggest the spatial variability in firn compaction rates is controlled by the recent patterns in accumulation rather than the long-term mean, so any firn corrections derived from a static long-term map will not generate the proper spatial patterns in compaction.
A realistic assessment of the relationship between the accumulation and compaction rates would employ compaction rates that sampled the same fraction of the total firn column compaction rates. To investigate the approximate fraction of total firn column compaction rates at multiple horizons of constant age (Fig. 7a) and depth (Fig. 7b), we use the Reference Herron and LangwayHerron and Langway (1980) steady-state densification model with a constant temperature and surface density and variable accumulation rates. Rather than plotting absolute compaction rates, we instead plot the fraction of total column compaction as determined by Sorge’s law (i.e. ḃ[1/ρ0 − 1/ρ i , where ḃ is the water-equivalent accumulation rate, ρ 0 is the initial density of the snow and ρ i is the density of ice; Reference BaderBader, 1954). Obviously and in both instances, the percentage of total column compaction increases with surveys to greater depths or ages. We are most interested, however, in the differences under various accumulation rates. Considering horizons of constant age (Fig. 7a) means that under all the accumulation rates, the firn has undergone compaction for the same amount of time. The firn in the higher- (lower-)accumulation regime, however, has accumulated more (less) snow and experienced larger (smaller) overburden pressure and compaction rates. Not surprisingly, the inverse is true when surveying to a horizon of constant depth (Fig. 7b): at greater depths, the firn in the lower- (higher-)accumulation regimes has spent more (less) time undergoing compaction and therefore, is more (less) dense.
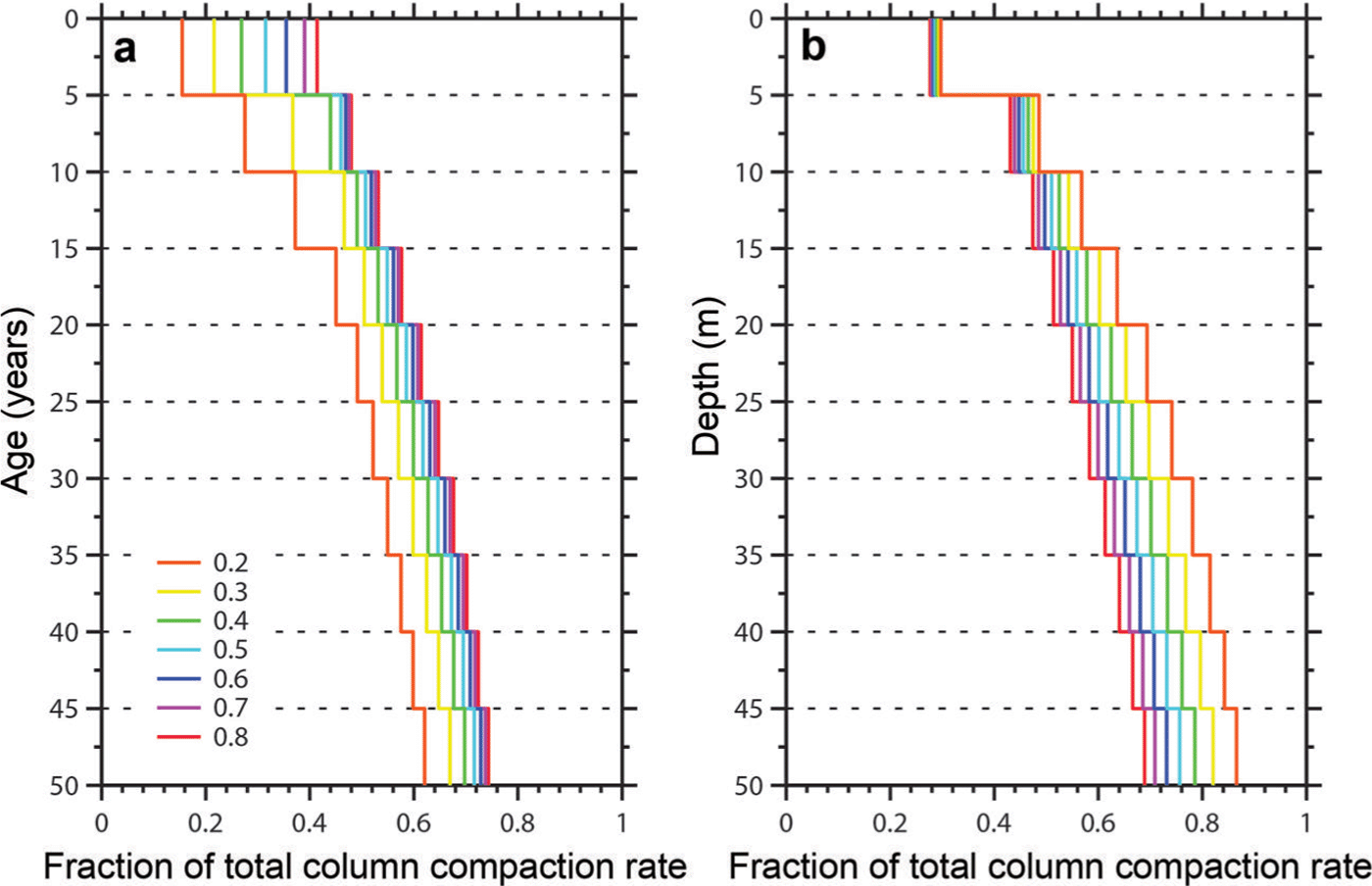
Fig. 7. Comparison of the fraction of the total column compaction rate relative to constant (a) age and (b) depth horizons. Each profile represents a different accumulation rate (see legend), ranging between 0.2 and 0.8 m w.e. a−1. The total column compaction rate was estimated using Sorge’s law (Reference BaderBader, 1954).
From Figure 7a, we see that surveying to greater ages, the range of the fraction of total column compaction under different accumulation regimes is reduced, whereas the opposite is true for surveys of constant depth. This result is due to the fact that the densification rate with depth is independent of the accumulation rate in the first stage of densification in the Reference Herron and LangwayHerron and Langway (1980) model, whereas in the second stage, the densification rate is dependent on the accumulation rate. At the same time, the densification rate with time during the first stage of densification is more dependent on the accumulation rate than in the second stage. For firn aged 30 years (i.e. the age of the oldest horizon used in this study) and accumulation rates equivalent to those measured (0.3–0.6 m w.e. a−1), the fraction of total column compaction ranges from 0.57 to 0.63. While this range suggests that compaction measurements from high-accumulation areas sample 6% more of the total column compaction, according to Sorge’s law total column compaction at an accumulation rate of 0.3 m w.e. a−1 is 50% of the compaction at 0.6 m w.e. a−1. Therefore, when sampling to 30-year-old firn, the impact of sampling to different depths resulting from variable accumulation rates is likely overshadowed by the actual variability in the compaction rate due to differing accumulation rates. Sampling to a constant depth of 30 m generates similar results: at an accumulation rate of 0.3 m w.e. a−1, the fraction of total column compaction surveyed is 0.70 as opposed to 0.62 for an accumulation rate of 0.6 m w.e. a−1. The main difference is that surveying to a constant depth results in a greater fraction of total column compaction rates for lower accumulation rates, the opposite of which is true for surveys to a constant age. Therefore, measuring to horizons of constant age does not greatly impact our interpretations, especially to older horizons, and surveys to constant depths have interpretation issues similar to those of surveys to constant ages, but the biases increase with depth.











