Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T17:52:55.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Bargaining in a Three-Person Game*

Published online by Cambridge University Press:  01 August 2014

William H. Riker
William H. Riker*
Affiliation:
University of Rochester
Get access Rights & Permissions [Opens in a new window]

Extract

Games are paradigms of many political events, especially those that involve partial or complete conflicts of interest among the participants. As paradigms, they display in relatively simple social interaction the same fundamental forces found in the more complex interactions of the grander political events whose structure they share. This is the feature of games that makes them attractive vehicles for both theorizing and experimentation in the social sciences. The scientific expectation is that, by studying the quasi-political interaction of games—where the variations among institutional, psychological, and ideological components of behavior are minimized—one will be able to understand more profoundly the basic political activities of bargaining, forming coalitions, and choosing strategies. This more profound understanding is a consequence of obtaining answers to the following questions:

(1) What is the mathematical solution, that is, what amount of utility can players be expected to obtain, when it is assumed that players are rational and wish to maximize utility?

(2) What is the strategy (or method of playing) that will ensure players of achieving the solution?

An answer to the first question indicates what may be anticipated as the outcome of political events. If we know it, then, if also we can assume players are rational maximizers of utility, we can predict the political future with some confidence. An answer to the second question (about strategies) permits political engineers to give advice to politicians about how to behave successfully.

Type
Research Article
Information
American Political Science Review , Volume 61 , Issue 3 , September 1967 , pp. 642 - 656
Copyright
Copyright © American Political Science Association 1967 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

The work reported in this essay was done under a grant from the National Science Foundation. It was originally reported at the American Political Science Association meeting, September, 1966. I am indebted to Professors William Gamson and Michael Maschler for advice and to several assistants for much faithful work, Robert Samberg, Robert Weber, and Peter Vivona.

References

1 See, especially, Neumann, John von and Morgenstern, Oskar, The Theory of Games and Economic Behavior (Princeton: Princeton University Press, 1947, 2nd edition)Google Scholar and the several volumes of Annals of Mathematics Studies devoted to the theory of games, Vola. 24, 28, 37, 39, 40, and 52.

2 Some exceptions that do aim at verifying and extending theory are Fouraker, L. E., “Level of Aspiration and Group Decision Making” in Messick, S. and Brayfield, A. H. (eds.), Decisions and Choice (New York: McGraw-Hill, 1964)Google Scholar; Gamson, W. A., “An Experimental Test of a Theory of Coalition Formation,” American Sociological Review, 26 (1961), 565–573 CrossRefGoogle Scholar; Maschler, Michael, Playing an n-Person Game: An Experiment (Princeton University: Econometric Research Program, Research Memorandum No. 73, 1 February 1965)Google Scholar; Rapoport, A. and Chammah, Albert M., Prisoners' Dilemma (Ann Arbor: University of Michigan Press, 1965)CrossRefGoogle Scholar; Schelling, Thomas, The Strategy of Conflict (Cambridge; Harvard University Press, 1960)Google Scholar; Leiserson, Michael, Coalitions in Politics (unpublished doctoral dissertation, Yale University, 1966).Google Scholar

3 Riker, William H., The Theory of Political Coalitions (New Haven: Yale University Press, 1963)Google Scholar, Chapter 1 and passim.

4 An example of a game in which some coalitions are not formable is: v(1) =v(2) =v(3) =v(1, 2, 3) =0; v(1, 2) =3.00; v(1, 3) =5.00; and v(2, 3) =20.00, in which 3 can always offer 2 more than 1 can so that (1, 2) can not be expected to form and in which 3 has no motive to form with 1 so that (1, 3) can not be expected to form either.

5 There are a number of other theories that offer other kinds of solutions to n-person games. They are not useful in the present context, however, so I will not discuss them here.

6 The points in addition to T in the von Neumann-Morgenstern solution are those which increase the payments of (1, 2) and (1, 3) continuously from $4.00 and $5.00 to $6.00. Since these additional points could not occur under the institutional arrangement of the game reported here, it is reasonable to limit the solution of this particular game to the set T.

7 Aumann, Robert J. and Maschler, Michael, “The Bargaining Set for Cooperative Games,” in Dresher, M., Shapley, L. S., and Tucker, A. W. (eds.), Advances in Game Theory (Princeton, N. J.: Princeton University Press, Annals of Mathematical Studies #52, 1964).Google Scholar This paper defines a bargaining set, M; a simpler (and here equivalent) set is M1(i), which is discussed in Davis, M. and Maschler, M., “Existence of Stable Payoff Configurations for Cooperative Games,” Bulletin of the American Mathematical Society, 69 (1963), 106–108.CrossRefGoogle Scholar See also Maschler, Michael, The Inequalities that Determine the Bargaining Set M1(i), (Jerusalem: Hebrew University, Research Program in Game Theory and Mathematical Economics, Research Memorandum #17, January, 1966, mimeographed).Google Scholar

8 Both the von Neumann-Morgenstern solution and the Aumann-Maschler bargaining set each differ from T by the inclusion of certain formal possibilities. As previously noted, the solution contains an infinity of additional and here institutionally impossible imputations. The bargaining set contains the i.r.p.c, x = (0, 0, 0), which arises when three single member coalitions or one three member coalition occur. It is included in the bargaining set only because the formal requirements of the definition of objections and stability require it. Since the additional imputations in the solution and the additional i.r.p.c. in the bargaining set are there for relisons of formal completeness rather than because they express some concept of stability, T may be regarded as the solution to this game with its particular institutional setting.

9 Riker, William H. and Niemi, Richard, “Anonymity and Rationality in the Essential Three-Person Game,” Human Relations, 17 (1964), 131–141 CrossRefGoogle Scholar.

10 Maschler, Michael, Playing an n-Person Game: An Experiment (Princeton University, Econometric Research Program, Research Memorandum No. 73, 1 February 1965).Google Scholar

11 Lieberman, Bernhardt, “Experimental Studies of Conflict in Some Two and Three Person Games,” in Criswell, J. H., et al. (eds.), Mathematical Methods in Small Group Processes (Stanford: Stanford University Press, 1962)Google Scholar and “i-Trust: A Notion of Trust in Three Person Games and International Affairs,” Research Memorandum SP-105-R (State University of New York at Stony Brook, October, 1963).

12 Incidentally, equal divisions never occurred in trials with Group III subjects, who were our most sophisticated players.

13 In Lieberman's experiments divisions comparable to x and y both occur well over half the time that the coalitions (1, 2) and (2, 3) occurred, while the division comparable to z occurs much less than half the time (1, 3) occurs. Presumably his subjects also sensed the inadequacy of U′ when it arose for them in its most extreme form.

14 The strategy of shaving the quota should not be confused with what Siegel and Fouraker have called the “level of aspiration.” See Fouraker, op. cit.; and Siegel, Sidney, “Levels of Aspiration and Decision-Making” Psychological Review, 64 (1957), 253–262.CrossRefGoogle ScholarPubMed The level of aspiration is a combination of individual utilities and available rewards. The notion of shaving the quota saya nothing about individual utilities for outcomes inasmuch as I assume, correctly in most trials of this game, that subjects have an overriding utility for winning (disregarding particular amounts) as against losing. Rather, the strategy of shaving is a purely instrumental device for winning.

15 χ 2 = 4.42.

16 χ 2 = 5.83.

17 The mechanism of producing a contretemps is as follows: If player 1 offers both 2 and 3 amounts greater than their quota or even if he offers just one other player his quota and the third more than his quota, he builds up their expectations so that when 2 and 3 face each other in the final conversation they each demand so much they cannot agree. Such disagreement is well illustrated by the course of negotiations in trial III-23 among sophisticated subjects. Proposed divisions are indicated by entries in each player's column.

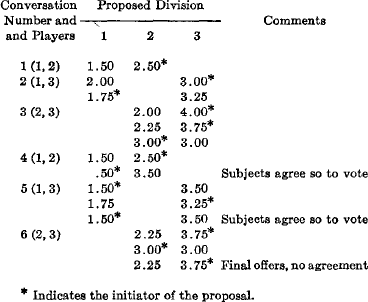
As this sequence displays, player 1's dramatic offer in the fourth conversation (which was accompanied by a fervent protestation that, playing in the institutionally weak position 1, he did not want to be left out altogether) simply confirmed player 2 in his attempt (displayed originally in conversation 3) to exact $3.00 from player 3 in the last conversation. On the other hand, player 1's firm insistence on the quota for player 3 encouraged 3 in his attempt to exact more than $3.50 from player 2. So 2 and 3 were unable to agree. They wanted in sum $6.75, while their coalition was worth only $6.00. Hence 1 and 3 voted for each other at x = (1.50, 0, 3.50) and 2 rather sulkily voted y = (0, 3.00, 3.00), which he knew 3 had not agreed to.

18 χ 2 = 16.41.

19 χ = 3.81.

20 χ 2 = 4.00.

21 The difference from expectation is χ 2 = 1.00, which few would regard as significant.

Submit a response

Comments

No Comments have been published for this article.