The expression for the induced velocity of a vortex element,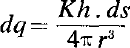 in Glauert's notation (where K is the strength of the vortex, h the length of the normal, and r the distance from the field point to the element, of length ds) which is often known as the Biot-Savart law, and is of fundamental importance in aerodynamics, is frequently left unproved in textbooks. Sometimes reference is made to the electro-magnetic analogy, or to a standard treatise such as Lamb. One well-known work implies that the law is the solution of an integral equation derived from the known induced velocity of an infinite straight-line vortex, but this is misleading, since there is an infinite number of solutions, of which only one is correct. Another textbook gives a lengthy argument starting from the replacement of a line vortex by a sheet of sources and sinks, which is probably not too convincing to the average student. Lamb himself gives a long and rather involved proof based on Helmholtz and Stokes, with appeals to the Theory of Attractions, with which few are likely to be familiar. A simple and direct proof from fluid mechanics seems therefore worth while.
in Glauert's notation (where K is the strength of the vortex, h the length of the normal, and r the distance from the field point to the element, of length ds) which is often known as the Biot-Savart law, and is of fundamental importance in aerodynamics, is frequently left unproved in textbooks. Sometimes reference is made to the electro-magnetic analogy, or to a standard treatise such as Lamb. One well-known work implies that the law is the solution of an integral equation derived from the known induced velocity of an infinite straight-line vortex, but this is misleading, since there is an infinite number of solutions, of which only one is correct. Another textbook gives a lengthy argument starting from the replacement of a line vortex by a sheet of sources and sinks, which is probably not too convincing to the average student. Lamb himself gives a long and rather involved proof based on Helmholtz and Stokes, with appeals to the Theory of Attractions, with which few are likely to be familiar. A simple and direct proof from fluid mechanics seems therefore worth while.