No CrossRef data available.
Published online by Cambridge University Press: 04 July 2016
Ghosh’s large-deflection hypersonic similitude and consequent plane and conico-annular piston theories have been applied to obtain unsteady pressure and the pitching moment derivatives for oscillating non-slender wedges, cones and ogives. The plane piston theory for a wedge is extended from a quasi-steady analysis, which gives the moment derivative due to pitch rate Cmq, to an unsteady analysis; the two analyses combine to give the moment derivative due to incidence rate 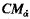 , which is shown here to be the same for wedges and quasi-wedges. The present theory can separately give Cmq and
, which is shown here to be the same for wedges and quasi-wedges. The present theory can separately give Cmq and 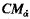 for a quasiwedge of arbitrary shape; this principle is illustrated for a particular quasi-wedge namely the parabolic arc plane ogive. In comparison, a previous theory by Hui gave only the sum of Cmq and
for a quasiwedge of arbitrary shape; this principle is illustrated for a particular quasi-wedge namely the parabolic arc plane ogive. In comparison, a previous theory by Hui gave only the sum of Cmq and 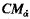 , only for wedges. The conico-annular piston theory is employed to obtain Cmθ, which is the moment derivative due to a steady pitch angle, and Cmq for non-slender cones and axisymmetric ogives in closed form for the first time.
, only for wedges. The conico-annular piston theory is employed to obtain Cmθ, which is the moment derivative due to a steady pitch angle, and Cmq for non-slender cones and axisymmetric ogives in closed form for the first time.