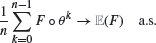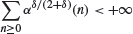Papers
Interdependence of directional quantities of planar tessellations
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 286-287
-
- Article
- Export citation
The distribution of volume reduction induced by isotropic projections
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 287-288
-
- Article
- Export citation
On stereological estimation of particle size distributions
-
- Published online by Cambridge University Press:
- 01 July 2016, p. 288
-
- Article
- Export citation
Determination of spherical area measures by means of dilation volumes
-
- Published online by Cambridge University Press:
- 01 July 2016, p. 289
-
- Article
- Export citation
Estimating parameters of point process models using the L-function
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 289-290
-
- Article
- Export citation
A third order point process characteristic
-
- Published online by Cambridge University Press:
- 01 July 2016, p. 290
-
- Article
- Export citation
Markov models in image analysis. An ophthalmic application
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 290-291
-
- Article
- Export citation
Random tessellation network and some inference problems
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 291-292
-
- Article
- Export citation
Gaussian measure and convex bodies
-
- Published online by Cambridge University Press:
- 01 July 2016, p. 292
-
- Article
- Export citation
Integral formulas for support functions and their use in the analysis of Boolean models
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 292-293
-
- Article
- Export citation
Methods for the analysis of replicated spatial point patterns in clinical neuro-anatomy
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-294
-
- Article
- Export citation
Statistics of windowed line segment processes
-
- Published online by Cambridge University Press:
- 01 July 2016, p. 294
-
- Article
- Export citation
Stochastic Geometry and Statistical Applications
On the Hausdorff distance between a convex set and an interior random convex hull
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 295-316
-
- Article
- Export citation
A diffusion model for bookstein triangle shape
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 317-334
-
- Article
- Export citation
On a random variable related to a system of convex bodies in the Euclidean space En
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 335-341
-
- Article
- Export citation
General Applied Probability
On the current enhancement at the edge of a crack in a lattice of resistors
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 342-364
-
- Article
- Export citation
Infinite block-structured transition matrices and their properties
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 365-384
-
- Article
- Export citation
Domain of attraction of quasi-stationary distributions for the brownian motion with drift
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 385-408
-
- Article
- Export citation
Trees with random conductivities and the (reciprocal) inverse Gaussian distribution
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 409-424
-
- Article
- Export citation
Rate of convergence for computing expectations of stopping functionals of an α-mixing process
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 425-448
-
- Article
- Export citation