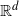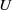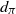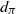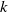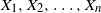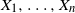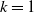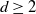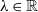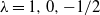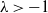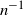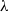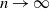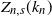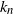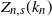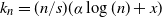April 2025: Stein's Method
Stein’s method is a powerful technique for assessing how closely one probability distribution approximates another. Introduced by Charles Stein in the 1970s for normal approximations to sums of random variables, it has since been successfully generalised to numerous distributions and applied across a broad spectrum of problems. The core idea is to identify an operator that characterises the target distribution, and then assess probabilistically how well the quantity of interest aligns with the properties encoded in this operator, typically through coupling constructions or Malliavin calculus. Using this operator to compare the two distributions yields quantifiable error bounds and rates of convergence, distinguishing Stein’s method from approaches that offer only qualitative statements or struggle with dependence.
Stein’s method has proved to be remarkably versatile. It has been applied in combinatorial problems, random graph theory, stochastic geometry, probabilistic number theory, concentration of measure, queueing theory, computational biology, and statistical mechanics, among many other areas. The method has also been extended to multivariate distributions, point processes, and process-level approximations. Its robustness in handling diverse forms of dependence makes it indispensable where independence assumptions fail. Today, Stein’s method is routinely used in many applications and has become a cornerstone of modern probability theory.
Collection created by Adrian Röllin (National University of Singapore)
Original Article
Normal approximation in total variation for statistics in geometric probability
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 03 July 2023, pp. 106-155
-
- Article
-
- You have access
- HTML
- Export citation
Multivariate Poisson and Poisson process approximations with applications to Bernoulli sums and
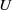 $U$
-statistics
$U$
-statistics
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 223-240
-
- Article
-
- You have access
- HTML
- Export citation
Normal Approximation for Functions of Hidden Markov Models
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 536-569
-
- Article
-
- You have access
- HTML
- Export citation
Arcsine laws for random walks generated from random permutations with applications to genomics
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 851-867
-
- Article
-
- You have access
- HTML
- Export citation
Stein’s method and approximating the multidimensional quantum harmonic oscillator
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 855-873
-
- Article
-
- You have access
- HTML
- Export citation
Limit laws for large
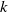 $k$
th-nearest neighbor balls
$k$
th-nearest neighbor balls
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / 2022
- Published online by Cambridge University Press:
- 06 July 2022, pp. 880-894
-
- Article
-
- You have access
- HTML
- Export citation
Research Papers
Trees grown under young-age preferential attachment
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 911-927
-
- Article
-
- You have access
- HTML
- Export citation
Original Article
Sub-tree counts on hyperbolic random geometric graphs
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1032-1069
-
- Article
-
- You have access
- HTML
- Export citation
Bounds for the chi-square approximation of the power divergence family of statistics
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 09 August 2022, pp. 1059-1080
-
- Article
-
- You have access
- HTML
- Export citation
Approaching the coupon collector’s problem with group drawings via Stein’s method
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1352-1366
-
- Article
-
- You have access
- HTML
- Export citation