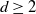1. Introduction
In this article, we study random geometric graphs on the d-dimensional Poincaré ball, a canonical model for negatively curved spaces in geometry [Reference Cannon, Floyd, Kenyon, Parry and Levy15, Reference Ratcliffe41]. Random geometric graphs were first studied in the 1960s, beginning with [Reference Gilbert24], as a model of radio communications. Since then, they have been a thriving topic of research in probability, statistical physics, and wireless networks (see [Reference Meester and Roy35, Reference Penrose38, Reference Yukich42, Reference Baccelli and Blaszczyszyn3, Reference Baccelli and Blaszczyszyn4, Reference Haenggi26]). In its simplest form, the random geometric graph can be constructed by taking a set of independent and identically distributed (i.i.d.) points
![]() ${\mathcal{X}}_n = \{X_1,\ldots,X_n\}$
on a metric space as its vertex set, and placing an edge between any two distinct points within a distance
${\mathcal{X}}_n = \{X_1,\ldots,X_n\}$
on a metric space as its vertex set, and placing an edge between any two distinct points within a distance
![]() $r_n$
. Most of the studies on such graphs assume that the underlying metric space is Euclidean or a compact and convex Euclidean subset. However, various applications, especially those in topological data analysis, necessitate more general metric spaces. For example, the extension to a compact manifold without boundary has recently been investigated in [Reference Bobrowski and Mukherjee8, Reference Bobrowski and Oliveira9, Reference De Kergorlay, Tillmann and Vipond18]. A crude one-line summary of these studies is that the behaviour of the graph on a ‘nice’ d-dimensional manifold is similar to that on a d-dimensional Euclidean space, though the proofs are technically more challenging and boundary effects need to be accounted for carefully.
$r_n$
. Most of the studies on such graphs assume that the underlying metric space is Euclidean or a compact and convex Euclidean subset. However, various applications, especially those in topological data analysis, necessitate more general metric spaces. For example, the extension to a compact manifold without boundary has recently been investigated in [Reference Bobrowski and Mukherjee8, Reference Bobrowski and Oliveira9, Reference De Kergorlay, Tillmann and Vipond18]. A crude one-line summary of these studies is that the behaviour of the graph on a ‘nice’ d-dimensional manifold is similar to that on a d-dimensional Euclidean space, though the proofs are technically more challenging and boundary effects need to be accounted for carefully.
Going beyond the class of nice d-dimensional manifolds with positive curvature and the Euclidean space with zero curvature, we focus on ‘negatively’ curved spaces in this paper. Such an investigation on hyperbolic spaces was initiated in [Reference Krioukov30]. Among many equivalent models for the hyperbolic space, we focus our attention on the widely used d-dimensional Poincaré ball. Apart from mathematical curiosity, a good reason for investigating hyperbolic geometric graphs lies in their properties such as sparsity, power-law degree distribution, small-world phenomena, and clustering. Such properties are often observed in complex networks. For more details, see the introductions in [Reference Krioukov30, Reference Gugelmann, Panagiotou and Peter25, Reference Fountoulakis20], where the graph is often referred to as the disk model or the KPKVB model after the authors of [Reference Krioukov30]. However, we always call it the hyperbolic random geometric graph. In a broader sense, our work is an addition to the developing literature on random structures of hyperbolic spaces (see [Reference Brooks and Makover12, Reference Benjamini and Schramm6, Reference Benjamini5, Reference Lyons and Peres34, Reference Lalley31, Reference Petri and Thaele40, Reference Cunningham, Zuev and Krioukov17, Reference Fountoulakis, van der Hoorn, Müller and Schepers21]).
The rest of the article is organized as follows. Sections 1.1 and 1.2 provide simulations on hyperbolic geometric graphs, and a preview of our results and their implications. In Section 2, we introduce our setup in detail and state all our results. We compare our results with those in the existing literature in Section 2.4, and Section 2.5 sketches results for analogous models in the Euclidean case. This is followed by the proofs in Section 3, where we introduce basic lemmas on the hyperbolic metric and measure and also the abstract normal approximation bound or second-order Poincaré inequality from [Reference Last, Peccati and Schulte32] needed for our central limit theorem (CLT).
1.1. Simulations on hyperbolic geometric graphs
We begin by introducing the Poincaré ball and the hyperbolic random geometric graph. Though there are other models of hyperbolic spaces, they are all isometric to the Poincaré ball (see [Reference Cannon, Floyd, Kenyon, Parry and Levy15, Section 7]); therefore, our results are essentially independent of the model selection. The d-dimensional Poincaré ball, denoted by
with negative curvature
![]() $-\zeta^2$
, is a d-dimensional open unit ball equipped with the Riemannian metric
$-\zeta^2$
, is a d-dimensional open unit ball equipped with the Riemannian metric
 \begin{equation} ds^2\,{:\!=}\, \frac{4}{\zeta^2} \frac{|dx|^2}{\big(1-|x|^2\big)^2} = \frac{4}{\zeta^2} \frac{dx_1^2 + \cdots + dx_d^2}{\big(1-x_1^2 - \cdots - x_d^2\big)^2} ,\end{equation}
\begin{equation} ds^2\,{:\!=}\, \frac{4}{\zeta^2} \frac{|dx|^2}{\big(1-|x|^2\big)^2} = \frac{4}{\zeta^2} \frac{dx_1^2 + \cdots + dx_d^2}{\big(1-x_1^2 - \cdots - x_d^2\big)^2} ,\end{equation}
where
![]() $|\cdot|$
denotes the Euclidean norm. Then, the hyperbolic distance between the origin (the same as the origin in the Euclidean plane) and
$|\cdot|$
denotes the Euclidean norm. Then, the hyperbolic distance between the origin (the same as the origin in the Euclidean plane) and
![]() $x\in B_d^{(\zeta)}$
is given by
$x\in B_d^{(\zeta)}$
is given by
![]() $d_\zeta(0,x) = \zeta^{-1} \log \big( (1+|x|)/(1-|x|) \big)$
, where
$d_\zeta(0,x) = \zeta^{-1} \log \big( (1+|x|)/(1-|x|) \big)$
, where
![]() $d_\zeta$
is the hyperbolic distance induced by (2). Though
$d_\zeta$
is the hyperbolic distance induced by (2). Though
![]() $B_d^{(\zeta)}$
is topologically the same as any open Euclidean ball, what matters to us is the metric itself. In the notation of (2), the Euclidean metric can be specified as
$B_d^{(\zeta)}$
is topologically the same as any open Euclidean ball, what matters to us is the metric itself. In the notation of (2), the Euclidean metric can be specified as
![]() $ds^2 = dx_1^2 + \cdots + dx_d^2$
, and so, on compact sets of the unit ball, the two metric elements differ only by a constant. This ensures that various geometric ingredients in the Euclidean case can be carried over to the Poincaré disk when restricted to a compact set of the unit ball. However, as
$ds^2 = dx_1^2 + \cdots + dx_d^2$
, and so, on compact sets of the unit ball, the two metric elements differ only by a constant. This ensures that various geometric ingredients in the Euclidean case can be carried over to the Poincaré disk when restricted to a compact set of the unit ball. However, as
![]() $|x| \uparrow 1$
in (2), one would expect that the geometry of the Poincaré disk significantly differs from that of the Euclidean disk; see Figure 1 for hyperbolic lines and circles on the Poincaré disk with
$|x| \uparrow 1$
in (2), one would expect that the geometry of the Poincaré disk significantly differs from that of the Euclidean disk; see Figure 1 for hyperbolic lines and circles on the Poincaré disk with
![]() $d=2$
. The reader may refer to [Reference Ratcliffe41] for a rigorous discussion of basic features of hyperbolic spaces and geometry.
$d=2$
. The reader may refer to [Reference Ratcliffe41] for a rigorous discussion of basic features of hyperbolic spaces and geometry.

Figure 1. Geodesic line segments and triangles (red lines), geodesic line segments of unit length (violet lines), and unit circles with centres on the Poincaré disk (green circles) with
![]() $\zeta = 1$
. These figures were drawn using the applet NonEuclid [Reference Castellanos and Darnell16].
$\zeta = 1$
. These figures were drawn using the applet NonEuclid [Reference Castellanos and Darnell16].
Let B(0, R) denote the hyperbolic ball of radius R centred at the origin. In addition to the curvature parameter
![]() $-\zeta^2$
in (2), our model involves a second curvature parameter
$-\zeta^2$
in (2), our model involves a second curvature parameter
![]() $-\alpha^2$
of another d-dimensional Poincaré ball
$-\alpha^2$
of another d-dimensional Poincaré ball
![]() $B_d^{(\alpha)}$
. We first choose a sequence of radii
$B_d^{(\alpha)}$
. We first choose a sequence of radii
![]() $R_n \to \infty$
as
$R_n \to \infty$
as
![]() $n \to \infty$
and select
$n \to \infty$
and select
![]() $N_n \stackrel{d}{=}$
Poisson(n) i.i.d. ‘uniform’ points
$N_n \stackrel{d}{=}$
Poisson(n) i.i.d. ‘uniform’ points
![]() $X_1,\ldots,X_{N_n}$
in
$X_1,\ldots,X_{N_n}$
in
![]() $B(0,R_n) \subset B_d^{(\alpha)}$
. Here, we mean ‘uniform’ with respect to the hyperbolic volume measure with curvature
$B(0,R_n) \subset B_d^{(\alpha)}$
. Here, we mean ‘uniform’ with respect to the hyperbolic volume measure with curvature
![]() $-\alpha^2$
. We then represent
$-\alpha^2$
. We then represent
![]() $X_i$
in the hyperbolic polar coordinates as
$X_i$
in the hyperbolic polar coordinates as
![]() $(r_i,\Theta_i)$
, where
$(r_i,\Theta_i)$
, where
![]() $r_i$
is the hyperbolic distance with respect to the curvature
$r_i$
is the hyperbolic distance with respect to the curvature
![]() $-\alpha^2$
, and
$-\alpha^2$
, and
![]() $\Theta_i \in [0,\pi]^{d-2} \times [0,2\pi)$
is a uniform random vector specifying angles. Next, we consider
$\Theta_i \in [0,\pi]^{d-2} \times [0,2\pi)$
is a uniform random vector specifying angles. Next, we consider
![]() $X_i = (r_i,\Theta_i)$
as the points of
$X_i = (r_i,\Theta_i)$
as the points of
![]() $B_d^{(\zeta)}$
by keeping their polar coordinates fixed, and connect any two points
$B_d^{(\zeta)}$
by keeping their polar coordinates fixed, and connect any two points
![]() $X_i,X_j$
if
$X_i,X_j$
if
![]() $0 < d_{\zeta}(X_i,X_j) < R_n$
. In other words, we sample points uniformly in a growing ball in
$0 < d_{\zeta}(X_i,X_j) < R_n$
. In other words, we sample points uniformly in a growing ball in
![]() $B_d^{(\alpha)}$
with respect to the hyperbolic volume measure with curvature
$B_d^{(\alpha)}$
with respect to the hyperbolic volume measure with curvature
![]() $-\alpha^2$
, and form a geometric graph on
$-\alpha^2$
, and form a geometric graph on
![]() $B_d^{(\zeta)}$
with respect to the hyperbolic metric with curvature
$B_d^{(\zeta)}$
with respect to the hyperbolic metric with curvature
![]() $-\zeta^2$
. We denote the resulting graph by
$-\zeta^2$
. We denote the resulting graph by
![]() $HG_n(R_n ;\ \alpha,\zeta)$
, for which four parameters are involved: the dimension d, two curvature paramaters
$HG_n(R_n ;\ \alpha,\zeta)$
, for which four parameters are involved: the dimension d, two curvature paramaters
![]() $\alpha$
and
$\alpha$
and
![]() $\zeta$
, and the radii regime
$\zeta$
, and the radii regime
![]() $R_n$
. As will be clarified in our later analyses, by choosing two distinct curvature parameters, one can construct a larger parametric family of random graphs with a richer set of features. We refer the reader to Remark 1 for a discussion about the dependence of our results on the individual parameters, not just their ratio, unlike many earlier results. After Definition 1, we briefly remark on the relationship of this model to the random geometric graph on a stationary Poisson process.
$R_n$
. As will be clarified in our later analyses, by choosing two distinct curvature parameters, one can construct a larger parametric family of random graphs with a richer set of features. We refer the reader to Remark 1 for a discussion about the dependence of our results on the individual parameters, not just their ratio, unlike many earlier results. After Definition 1, we briefly remark on the relationship of this model to the random geometric graph on a stationary Poisson process.
Figure 2 presents five simulation results with
![]() $d = 2$
,
$d = 2$
,
![]() $n = 1000$
,
$n = 1000$
,
![]() $\zeta = 1$
,
$\zeta = 1$
,
![]() $R_n = 2\log 1000 = 13.82$
, and different choices of
$R_n = 2\log 1000 = 13.82$
, and different choices of
![]() $\alpha$
. It is useful to keep in mind that for a small
$\alpha$
. It is useful to keep in mind that for a small
![]() $\alpha$
, the space is closer to the Euclidean space, in the sense that more points are scattered near the centre. For a large
$\alpha$
, the space is closer to the Euclidean space, in the sense that more points are scattered near the centre. For a large
![]() $\alpha$
, the points near the boundary mainly dominate the asymptotics. Furthermore, by the geometry of a hyperbolic space, the points near the centre easily connect to many other points, and so the presence of such points will change the connectivity structure. Additionally, we may notice a phase transition in the connectivity at
$\alpha$
, the points near the boundary mainly dominate the asymptotics. Furthermore, by the geometry of a hyperbolic space, the points near the centre easily connect to many other points, and so the presence of such points will change the connectivity structure. Additionally, we may notice a phase transition in the connectivity at
![]() $\alpha = 1$
, due to the appearance of points closer to the centre. Some of the above observations will be crystallized later as rigorous theorems, while many more still await exploration in future works. We now preview some of our results and place them in the context of the growing literature on hyperbolic random geometric graphs.
$\alpha = 1$
, due to the appearance of points closer to the centre. Some of the above observations will be crystallized later as rigorous theorems, while many more still await exploration in future works. We now preview some of our results and place them in the context of the growing literature on hyperbolic random geometric graphs.

Figure 2. Simulations of
![]() $HG_{1000}(R_{1000} ;\ \alpha, 1)$
for
$HG_{1000}(R_{1000} ;\ \alpha, 1)$
for
![]() $d = 2$
with
$d = 2$
with
![]() $R_{1000}=2\log 1000 = 13.82$
and different values of
$R_{1000}=2\log 1000 = 13.82$
and different values of
![]() $\alpha$
. Isolated vertices have been omitted.
$\alpha$
. Isolated vertices have been omitted.
1.2. Tree-like hierarchical structures: a preview of our results and some implications
One of the main characteristics of hyperbolic random geometric graphs is the presence of tree-like hierarchical structures, implying that the vertices on
![]() $B_d^{(\zeta)}$
are classified into large groups of smaller subgroups, which themselves consist of further smaller subgroups (see [Reference Krioukov30]). This is reflected in our simulations, illustrating that, as compared to the Euclidean spaces, the non-amenability of a negatively curved space enables one to embed many more trees in the space.
$B_d^{(\zeta)}$
are classified into large groups of smaller subgroups, which themselves consist of further smaller subgroups (see [Reference Krioukov30]). This is reflected in our simulations, illustrating that, as compared to the Euclidean spaces, the non-amenability of a negatively curved space enables one to embed many more trees in the space.
The study of the hyperbolic random geometric graph started with [Reference Krioukov30]. Since then, various features of the resulting graph have been investigated intensively by many authors. Indeed, there are a number of publications on the subject, in areas including the structure of large components [Reference Bode, Fountoulakis and Müller10, Reference Fountoulakis and Müller22, Reference Kiwi and Mitsche29], the probability of connectivity [Reference Bode, Fountoulakis and Müller11], clique-counts [Reference Bläsius, Friedrich and Krohmer7], the degree sequence and clustering [Reference Candellero and Fountoulakis14, Reference Gugelmann, Panagiotou and Peter25, Reference Fountoulakis, van der Hoorn, Müller and Schepers21], the bootstrap percolation process [Reference Candellero and Fountoulakis13], the typical distances and diameter of components [Reference Abdullah, Bode and Fountoulakis1, Reference Kiwi and Mitsche27, Reference Müller and Staps36], and the spectral properties of the graph [Reference Kiwi and Mitsche28]. More recently, [Reference Fountoulakis and Yukich23] has proved expectation and variance asymptotics as well as CLTs for the number of isolated and extreme points for the hyperbolic random geometric graph.
The earlier studies cited above, however, treat only a special case, namely,
for some
![]() $\nu\in (0,\infty)$
, or similar variants. In contrast, the current study assumes a set of conditions more general than (3). For example, we allow for a general dimension d, and we do not put any restrictive conditions on
$\nu\in (0,\infty)$
, or similar variants. In contrast, the current study assumes a set of conditions more general than (3). For example, we allow for a general dimension d, and we do not put any restrictive conditions on
![]() $R_n$
as in (3). Under this general setup, the primary objective of this paper is to uncover the spatial distribution of the tree-like structure via sub-tree counts, i.e., the number of copies of a given tree in
$R_n$
as in (3). Under this general setup, the primary objective of this paper is to uncover the spatial distribution of the tree-like structure via sub-tree counts, i.e., the number of copies of a given tree in
![]() $HG_n(R_n ;\ \alpha, \zeta)$
. In graph-theoretic language, we count the number of injective graph homomorphisms from a fixed sub-tree to
$HG_n(R_n ;\ \alpha, \zeta)$
. In graph-theoretic language, we count the number of injective graph homomorphisms from a fixed sub-tree to
![]() $HG_n(R_n ;\ \alpha, \zeta)$
. Our main results in Theorems 1, 2, and 3 establish expectation asymptotics, variance asymptotics, and the normal approximation bounds for the sub-tree counts. All of our asymptotic results crucially depend on a degree sequence of the tree under consideration as well as the two curvature parameters
$HG_n(R_n ;\ \alpha, \zeta)$
. Our main results in Theorems 1, 2, and 3 establish expectation asymptotics, variance asymptotics, and the normal approximation bounds for the sub-tree counts. All of our asymptotic results crucially depend on a degree sequence of the tree under consideration as well as the two curvature parameters
![]() $-\zeta^2$
and
$-\zeta^2$
and
![]() $-\alpha^2$
.
$-\alpha^2$
.
More specifically, the present paper studies a more general sub-tree count, denoted by
![]() $S_n^{(\gamma)}$
,
$S_n^{(\gamma)}$
,
![]() $\gamma\in (0,1]$
, which counts sub-trees only on the space
$\gamma\in (0,1]$
, which counts sub-trees only on the space
![]() $B(0,R_n)\setminus \mathring{B}(0, (1-\gamma)R_n)$
. In other words,
$B(0,R_n)\setminus \mathring{B}(0, (1-\gamma)R_n)$
. In other words,
![]() $S_n^{(\gamma)}$
counts sub-trees in an annulus with inner radius
$S_n^{(\gamma)}$
counts sub-trees in an annulus with inner radius
![]() $(1-\gamma)R_n$
and outer radius
$(1-\gamma)R_n$
and outer radius
![]() $R_n$
. In particular,
$R_n$
. In particular,
![]() $S_n\,{:\!=}\,S_n^{(1)}$
denotes the sub-tree counts for the ‘entire’ space
$S_n\,{:\!=}\,S_n^{(1)}$
denotes the sub-tree counts for the ‘entire’ space
![]() $B(0,R_n)$
. Our results will reveal that if
$B(0,R_n)$
. Our results will reveal that if
![]() $\alpha$
is sufficiently large, i.e., the space
$\alpha$
is sufficiently large, i.e., the space
![]() $B_d^{(\alpha)}$
is sufficiently hyperbolic (for example,
$B_d^{(\alpha)}$
is sufficiently hyperbolic (for example,
![]() $\alpha=1.2$
in Figure 2), then the asymptotics of
$\alpha=1.2$
in Figure 2), then the asymptotics of
![]() $S_n^{(\gamma)}$
does not depend on
$S_n^{(\gamma)}$
does not depend on
![]() $\gamma$
. In other words, the spatial distribution of sub-trees is mostly determined by those near the boundary of
$\gamma$
. In other words, the spatial distribution of sub-trees is mostly determined by those near the boundary of
![]() $B(0,R_n)$
. In this case,
$B(0,R_n)$
. In this case,
![]() $S_n$
is well approximated by
$S_n$
is well approximated by
![]() $S_n^{(\gamma)}$
for any
$S_n^{(\gamma)}$
for any
![]() $\gamma \in (0,1)$
. On the other hand, if
$\gamma \in (0,1)$
. On the other hand, if
![]() $\alpha$
is small, as in Figure 2 with
$\alpha$
is small, as in Figure 2 with
![]() $\alpha=0.8$
, the distribution of sub-trees will be affected by those near the centre of the space, and
$\alpha=0.8$
, the distribution of sub-trees will be affected by those near the centre of the space, and
![]() $S_n^{(\gamma)}$
no longer approximates
$S_n^{(\gamma)}$
no longer approximates
![]() $S_n$
. To relate the above phenomena to the context of previous studies, Corollary 2 restates our results in the special case when
$S_n$
. To relate the above phenomena to the context of previous studies, Corollary 2 restates our results in the special case when
![]() $R_n = 2(\zeta (d-1))^{-1} \log (n/\nu)$
. If
$R_n = 2(\zeta (d-1))^{-1} \log (n/\nu)$
. If
![]() $d = 2$
, this clearly reduces to (3). Interested readers wishing to understand this special case can proceed directly to Section 2.4. In particular, Table 1 compares a part of our results with those of earlier works on connectivity, percolation, and clique counts. If we take the tree to be a single edge, then
$d = 2$
, this clearly reduces to (3). Interested readers wishing to understand this special case can proceed directly to Section 2.4. In particular, Table 1 compares a part of our results with those of earlier works on connectivity, percolation, and clique counts. If we take the tree to be a single edge, then
![]() $S_n$
denotes the number of edges. Our results restricted to this case are consistent with the power-law behaviour for degree distributions. Our results also indicate a similar power-law behaviour for more general sub-tree counts, revealing the dependence of the exponents on the degree sequence of the tree under consideration and the parameters
$S_n$
denotes the number of edges. Our results restricted to this case are consistent with the power-law behaviour for degree distributions. Our results also indicate a similar power-law behaviour for more general sub-tree counts, revealing the dependence of the exponents on the degree sequence of the tree under consideration and the parameters
![]() $\alpha,\zeta$
. This is also explained in detail in Section 2.4.
$\alpha,\zeta$
. This is also explained in detail in Section 2.4.
Table 1. Summary of related results for
![]() $d = 2$
,
$d = 2$
,
![]() $\zeta = 1$
,
$\zeta = 1$
,
![]() $R_n = 2 \log (n/\nu)$
,
$R_n = 2 \log (n/\nu)$
,
![]() $\nu \in (0,\infty)$
. Here
$\nu \in (0,\infty)$
. Here
![]() $K_k$
denotes the number of k-cliques in
$K_k$
denotes the number of k-cliques in
![]() $HG_n(R_n ; \alpha, 1)$
,
$HG_n(R_n ; \alpha, 1)$
,
![]() $\mathbb{P}_{conn} = \mathbb{P}(HG_n(R_n ; \alpha, 1)\ \mathrm{is connected})$
, and
$\mathbb{P}_{conn} = \mathbb{P}(HG_n(R_n ; \alpha, 1)\ \mathrm{is connected})$
, and
![]() $\mathbb{P}_{perc} = \mathbb{P}(HG_n(R_n ; \alpha, 1)\ \mathrm{percolates})$
, where, by percolation, we mean the existence of a giant component, i.e., a component of size
$\mathbb{P}_{perc} = \mathbb{P}(HG_n(R_n ; \alpha, 1)\ \mathrm{percolates})$
, where, by percolation, we mean the existence of a giant component, i.e., a component of size
![]() $\Theta(n)$
.
$\Theta(n)$
.

Let us now add a few words on our proofs. The expectation and variance asymptotics for sub-tree counts involve the Mecke formula for Poisson point processes and various estimates for the measure and metric on the Poincaré ball. By virtue of the tree assumption, the relative angles between points will exhibit sufficient independence (see Lemma 2). For the CLT, we use the abstract normal approximation result (see [Reference Last, Peccati and Schulte32]) based on the Malliavin–Stein method. To use this result, we derive detailed bounds on the first- (add-one cost) and second-order difference operators of the sub-tree counts. In many applications to Euclidean stochastic geometric functionals, the first- and second-order difference operators are bounded by a constant, but in our setup, the bounds for these operators are unbounded in n. Nevertheless, we manage to apply [Reference Last, Peccati and Schulte32] by carefully bounding the difference operators, so that their growth is dominated by our variance lower bounds (see Remark 3(iii)).
2. Our setup and results
2.1. The Poincaré ball
Our underlying metric space is the d-dimensional Poincaré ball
![]() $B_d^{(\zeta)}$
in (1), which is equipped with the Riemannian metric (2), where
$B_d^{(\zeta)}$
in (1), which is equipped with the Riemannian metric (2), where
![]() $-\zeta^2$
represents the negative (Gaussian) curvature with
$-\zeta^2$
represents the negative (Gaussian) curvature with
![]() $\zeta > 0$
. This is a standard model in the literature, but earlier studies (e.g. [Reference Bode, Fountoulakis and Müller10, Reference Fountoulakis and Müller22, Reference Kiwi and Mitsche29, Reference Bode, Fountoulakis and Müller11, Reference Bläsius, Friedrich and Krohmer7, Reference Candellero and Fountoulakis14, Reference Gugelmann, Panagiotou and Peter25, Reference Candellero and Fountoulakis13, Reference Kiwi and Mitsche27, Reference Müller and Staps36, Reference Kiwi and Mitsche28, Reference Fountoulakis and Yukich23, Reference Abdullah, Bode and Fountoulakis1, Reference Fountoulakis19, Reference Fountoulakis20]) treated only the special case
$\zeta > 0$
. This is a standard model in the literature, but earlier studies (e.g. [Reference Bode, Fountoulakis and Müller10, Reference Fountoulakis and Müller22, Reference Kiwi and Mitsche29, Reference Bode, Fountoulakis and Müller11, Reference Bläsius, Friedrich and Krohmer7, Reference Candellero and Fountoulakis14, Reference Gugelmann, Panagiotou and Peter25, Reference Candellero and Fountoulakis13, Reference Kiwi and Mitsche27, Reference Müller and Staps36, Reference Kiwi and Mitsche28, Reference Fountoulakis and Yukich23, Reference Abdullah, Bode and Fountoulakis1, Reference Fountoulakis19, Reference Fountoulakis20]) treated only the special case
![]() $d=2$
, whereas we allow for higher dimensions as well. We mention some of the basic properties of this metric space, and some more will be stated in Section 3.1. For more details on the Poincaré ball, we refer the reader to [Reference Ratcliffe41, Reference Anderson2], while [Reference Cannon, Floyd, Kenyon, Parry and Levy15] is a good resource for a quick reading. In what follows, we often represent the point
$d=2$
, whereas we allow for higher dimensions as well. We mention some of the basic properties of this metric space, and some more will be stated in Section 3.1. For more details on the Poincaré ball, we refer the reader to [Reference Ratcliffe41, Reference Anderson2], while [Reference Cannon, Floyd, Kenyon, Parry and Levy15] is a good resource for a quick reading. In what follows, we often represent the point
![]() $x \in B_d^{(\zeta)}$
in terms of ‘hyperbolic’ polar coordinates: for
$x \in B_d^{(\zeta)}$
in terms of ‘hyperbolic’ polar coordinates: for
![]() $x \in B_d^{(\zeta)}$
, we write
$x \in B_d^{(\zeta)}$
, we write
![]() $x = (r,\theta_1,\dots, \theta_{d-1})$
, where
$x = (r,\theta_1,\dots, \theta_{d-1})$
, where
![]() $r\geq 0$
is the radial part of x, defined by
$r\geq 0$
is the radial part of x, defined by
and
![]() $(\theta_1, \dots, \theta_{d-1}) \in C_d \,{:\!=}\, [0,\pi]^{d-2} \times [0,2\pi)$
is the angular part of x. Let
$(\theta_1, \dots, \theta_{d-1}) \in C_d \,{:\!=}\, [0,\pi]^{d-2} \times [0,2\pi)$
is the angular part of x. Let
![]() $d_\zeta$
denote the hyperbolic distance induced by (2); then it satisfies
$d_\zeta$
denote the hyperbolic distance induced by (2); then it satisfies
![]() $d_\zeta(0,x)= r$
.
$d_\zeta(0,x)= r$
.
Using the hyperbolic polar coordinates
![]() $(r,\theta_1,\dots,\theta_{d-1})$
, the metric (2) can be rewritten as
$(r,\theta_1,\dots,\theta_{d-1})$
, the metric (2) can be rewritten as
 \begin{equation}ds^2 = dr^2 + \Bigg( \frac{\sinh (\zeta r)}{\zeta} \Bigg)^2 \bigg( d\theta_1^2 + \sum_{k=2}^{d-1} \prod_{i=1}^{k-1} \sin^2 \theta_i \, d\theta_k^2 \bigg),\end{equation}
\begin{equation}ds^2 = dr^2 + \Bigg( \frac{\sinh (\zeta r)}{\zeta} \Bigg)^2 \bigg( d\theta_1^2 + \sum_{k=2}^{d-1} \prod_{i=1}^{k-1} \sin^2 \theta_i \, d\theta_k^2 \bigg),\end{equation}
from which we obtain the volume element,
 \begin{align*}dV = \left( \frac{\sinh (\zeta r)}{\zeta} \right)^{d-1}\prod_{i=1}^{d-2} \sin^{d-i-1} \theta_i\, dr\, d\theta_1 \dots d\theta_{d-1}.\end{align*}
\begin{align*}dV = \left( \frac{\sinh (\zeta r)}{\zeta} \right)^{d-1}\prod_{i=1}^{d-2} \sin^{d-i-1} \theta_i\, dr\, d\theta_1 \dots d\theta_{d-1}.\end{align*}
We now generate ‘quasi-uniform’ random points on a sequence of growing compact subsets of the Poincaré ball. First, we choose a deterministic sequence
![]() $R_n$
,
$R_n$
,
![]() $n\geq1$
, which grows to infinity as
$n\geq1$
, which grows to infinity as
![]() $n\to\infty$
. We assume that the angular part of the random points is uniformly chosen from the density,
$n\to\infty$
. We assume that the angular part of the random points is uniformly chosen from the density,
where we have set
![]() $\kappa_m= \int_0^{\pi} \sin^m \theta\, d\theta$
, and trivially,
$\kappa_m= \int_0^{\pi} \sin^m \theta\, d\theta$
, and trivially,
![]() $\kappa_0 = \pi$
. We use the symbol
$\kappa_0 = \pi$
. We use the symbol
![]() $\pi$
to denote the angular density as well as the famed constant, but the context makes it clear which of them we refer to. Given another curvature parameter
$\pi$
to denote the angular density as well as the famed constant, but the context makes it clear which of them we refer to. Given another curvature parameter
![]() $\alpha > 0$
, we assume that the density of the radial part is
$\alpha > 0$
, we assume that the density of the radial part is
This density is described as the ratio of the surface area of B(0, r) to the volume of
![]() $B(0,R_n)$
, where B(0, r) and
$B(0,R_n)$
, where B(0, r) and
![]() $B(0,R_n)$
are both defined on
$B(0,R_n)$
are both defined on
![]() $B_d^{(\alpha)}$
. So the density (6) can be regarded as a uniform density (for the radial part) on
$B_d^{(\alpha)}$
. So the density (6) can be regarded as a uniform density (for the radial part) on
![]() $B_d^{(\alpha)}$
. Combining (5) and (6), we can generate uniform random points on
$B_d^{(\alpha)}$
. Combining (5) and (6), we can generate uniform random points on
![]() $B_d^{(\alpha)}$
. Since their radial coordinates are bounded by
$B_d^{(\alpha)}$
. Since their radial coordinates are bounded by
![]() $R_n$
, we can also consider them as points in
$R_n$
, we can also consider them as points in
![]() $B(0,R_n) \subset B_d^{(\alpha)}$
. By using the same hyperbolic polar coordinates, i.e., the same radial and angular coordinates, we now represent these points in
$B(0,R_n) \subset B_d^{(\alpha)}$
. By using the same hyperbolic polar coordinates, i.e., the same radial and angular coordinates, we now represent these points in
![]() $B_d^{(\zeta)}$
as well, and construct the hyperbolic geometric graph in
$B_d^{(\zeta)}$
as well, and construct the hyperbolic geometric graph in
![]() $B_d^{(\zeta)}$
. Specifically, we connect any two distinct points
$B_d^{(\zeta)}$
. Specifically, we connect any two distinct points
![]() $X_i$
,
$X_i$
,
![]() $X_j$
if
$X_j$
if
![]() $0< d_\zeta(X_i,X_j)\le R_n$
. Obviously, (6) is no longer a uniform density (for the radial part) on
$0< d_\zeta(X_i,X_j)\le R_n$
. Obviously, (6) is no longer a uniform density (for the radial part) on
![]() $B_d^{(\zeta)}$
, unless
$B_d^{(\zeta)}$
, unless
![]() $\zeta = \alpha$
; it is called ‘quasi-uniform’.
$\zeta = \alpha$
; it is called ‘quasi-uniform’.
Though the probability density in (6) looks a little complicated, we shall mostly resort to the following useful approximation. Set
![]() $T\,{:\!=}\, R_n-d_\zeta(0,X)$
, where X is a random point with density
$T\,{:\!=}\, R_n-d_\zeta(0,X)$
, where X is a random point with density
![]() $\rho_{n,\alpha} \otimes \pi$
. Denote by
$\rho_{n,\alpha} \otimes \pi$
. Denote by
![]() $\bar \rho_{n,\alpha} (t)$
the density of T; i.e.,
$\bar \rho_{n,\alpha} (t)$
the density of T; i.e.,
 \begin{equation}\bar \rho_{n,\alpha} (t) = \frac{\sinh^{d-1}\bigl(\alpha (R_n-t)\bigr)}{\int_0^{R_n} \sinh^{d-1} (\alpha s) ds}, \ \ 0 \leq t \leq R_n.\end{equation}
\begin{equation}\bar \rho_{n,\alpha} (t) = \frac{\sinh^{d-1}\bigl(\alpha (R_n-t)\bigr)}{\int_0^{R_n} \sinh^{d-1} (\alpha s) ds}, \ \ 0 \leq t \leq R_n.\end{equation}
In the sequel, we often denote a random point X with density
![]() $\rho_{n,\alpha} \otimes \pi$
by its hyperbolic polar coordinates
$\rho_{n,\alpha} \otimes \pi$
by its hyperbolic polar coordinates
![]() $X=(T, \Theta)$
, where
$X=(T, \Theta)$
, where
![]() $\Theta$
is the angular part, and the radial part is described by T rather than
$\Theta$
is the angular part, and the radial part is described by T rather than
![]() $d_\zeta(0,X)$
. The approximation result below was established for
$d_\zeta(0,X)$
. The approximation result below was established for
![]() $d=2$
in [Reference Candellero and Fountoulakis14]. The proof is in Section 3.
$d=2$
in [Reference Candellero and Fountoulakis14]. The proof is in Section 3.
Lemma 1.
-
(i) As
 $n\to\infty$
, we have uniformly for
$n\to\infty$
, we have uniformly for \begin{align*}\bar \rho_{n,\alpha} (t) \leq \bigl( 1+o(1) \bigr) \alpha (d-1) e^{-\alpha (d-1)t}\end{align*}
\begin{align*}\bar \rho_{n,\alpha} (t) \leq \bigl( 1+o(1) \bigr) \alpha (d-1) e^{-\alpha (d-1)t}\end{align*}
 $0 \leq t < R_n$
.
$0 \leq t < R_n$
.
-
(ii) For every
 $0 < \lambda <1$
, we have, as
$0 < \lambda <1$
, we have, as
 $n\to \infty$
, uniformly for
$n\to \infty$
, uniformly for \begin{align*}\bar \rho_{n,\alpha} (t) =\bigl( 1+o(1) \bigr) \alpha (d-1) e^{-\alpha (d-1)t}\end{align*}
\begin{align*}\bar \rho_{n,\alpha} (t) =\bigl( 1+o(1) \bigr) \alpha (d-1) e^{-\alpha (d-1)t}\end{align*}
 $0 \leq t \leq \lambda R_n$
.
$0 \leq t \leq \lambda R_n$
.
More concretely, this lemma claims that if t is restricted to
![]() $[0,\lambda R_n]$
for some fixed
$[0,\lambda R_n]$
for some fixed
![]() $\lambda\in(0,1)$
, then
$\lambda\in(0,1)$
, then
![]() $\bar \rho_{n,\alpha} (t)$
is asymptotically and uniformly equal to
$\bar \rho_{n,\alpha} (t)$
is asymptotically and uniformly equal to
![]() $\alpha (d-1) e^{-\alpha (d-1)t}$
. If there is no such restriction on the range of t, we can only bound
$\alpha (d-1) e^{-\alpha (d-1)t}$
. If there is no such restriction on the range of t, we can only bound
![]() $\bar \rho_{n,\alpha} (t)$
, up to constant factors, by the same quantity. For the exact asymptotics of
$\bar \rho_{n,\alpha} (t)$
, up to constant factors, by the same quantity. For the exact asymptotics of
![]() $\bar \rho_{n,\alpha} (t)$
, we apply the result in Case (ii), while Case (i) is used for bounding
$\bar \rho_{n,\alpha} (t)$
, we apply the result in Case (ii), while Case (i) is used for bounding
![]() $\bar \rho_{n,\alpha} (t)$
.
$\bar \rho_{n,\alpha} (t)$
.
Now we define our main object of interest, the hyperbolic random geometric graph. The first ingredient is the Poisson point process on
![]() $B_d^{(\zeta)}$
. For every
$B_d^{(\zeta)}$
. For every
![]() $n \geq1$
, let
$n \geq1$
, let
![]() $(X_i, \, i \geq 1)$
be a sequence of i.i.d. random points on
$(X_i, \, i \geq 1)$
be a sequence of i.i.d. random points on
![]() $B_d^{(\zeta)}$
with common density
$B_d^{(\zeta)}$
with common density
![]() $\rho_{n,\alpha} \otimes \pi$
. Letting
$\rho_{n,\alpha} \otimes \pi$
. Letting
![]() $N_n$
be a Poisson random variable with mean n, independent of
$N_n$
be a Poisson random variable with mean n, independent of
![]() $(X_i)$
, one can construct the Poisson point process
$(X_i)$
, one can construct the Poisson point process
![]() $\mathcal{P}_n = \{ X_1, X_2, \dots, X_{N_n}\}$
whose intensity measure is
$\mathcal{P}_n = \{ X_1, X_2, \dots, X_{N_n}\}$
whose intensity measure is
![]() $n (\rho_{n,\alpha} \otimes \pi)$
.
$n (\rho_{n,\alpha} \otimes \pi)$
.
Definition 1. (Hyperbolic random geometric graph) Let
![]() $R_n \to \infty$
as
$R_n \to \infty$
as
![]() $n \to \infty$
. The hyperbolic random geometric graph
$n \to \infty$
. The hyperbolic random geometric graph
![]() $HG_n(R_n ;\ \alpha, \zeta)$
is a simple, undirected graph whose vertex set is the Poisson point process
$HG_n(R_n ;\ \alpha, \zeta)$
is a simple, undirected graph whose vertex set is the Poisson point process
![]() $\mathcal{P}_n$
with intensity measure
$\mathcal{P}_n$
with intensity measure
![]() $n (\rho_{n,\alpha}\otimes \pi)$
, and whose edge set is
$n (\rho_{n,\alpha}\otimes \pi)$
, and whose edge set is
![]() $\{ (X_i,X_j) : X_i,X_j \in \mathcal{P}_n, 0 < d_\zeta(X_i,X_j) \leq R_n \}$
.
$\{ (X_i,X_j) : X_i,X_j \in \mathcal{P}_n, 0 < d_\zeta(X_i,X_j) \leq R_n \}$
.
Finally, we remark that even if
![]() $\alpha = \zeta$
, the process
$\alpha = \zeta$
, the process
![]() $\mathcal{P}_n$
is not the restriction of a stationary Poisson process to
$\mathcal{P}_n$
is not the restriction of a stationary Poisson process to
![]() $B_d^{(\alpha)}$
unless
$B_d^{(\alpha)}$
unless
![]() $|B(0,R_n)| = n$
. A random geometric graph on a stationary Poisson process is a different model, which is actually beyond the scope of this article.
$|B(0,R_n)| = n$
. A random geometric graph on a stationary Poisson process is a different model, which is actually beyond the scope of this article.
2.2. Expectation and variance asymptotics for sub-tree counts
We introduce the notion of a graph homomorphism to define our sub-tree counts. Suppose H is a simple graph on
![]() $[k]\,{:\!=}\,\{ 1,\dots,k \}$
with edge set E(H). Given another simple graph
$[k]\,{:\!=}\,\{ 1,\dots,k \}$
with edge set E(H). Given another simple graph
![]() $G = (V(G),E(G))$
, a graph homomorphism from H to G refers to a function
$G = (V(G),E(G))$
, a graph homomorphism from H to G refers to a function
![]() $f : [k] \to V(G)$
such that if
$f : [k] \to V(G)$
such that if
![]() $(i,j) \in E(H)$
, then
$(i,j) \in E(H)$
, then
![]() $(f(i),f(j)) \in E(G)$
, i.e., the adjacency relation is preserved. We denote by
$(f(i),f(j)) \in E(G)$
, i.e., the adjacency relation is preserved. We denote by
![]() ${\mathcal{C}} (H,G)$
the number of injective graph homomorphisms from H to G, i.e., of functions f as above that are injective homomorphisms. Informally,
${\mathcal{C}} (H,G)$
the number of injective graph homomorphisms from H to G, i.e., of functions f as above that are injective homomorphisms. Informally,
![]() ${\mathcal{C}} (H,G)$
counts the number of copies of H in G. This can be represented easily as follows:
${\mathcal{C}} (H,G)$
counts the number of copies of H in G. This can be represented easily as follows:
 \begin{equation}{\mathcal{C}}(H,G) = \sum_{(v_1,\ldots,v_k) \in V(G)}^{\neq} \prod_{(i,j) \in E(H)} {\textbf{1}} \bigl\{ \, (v_i,v_j) \in E(G)\, \bigr\},\end{equation}
\begin{equation}{\mathcal{C}}(H,G) = \sum_{(v_1,\ldots,v_k) \in V(G)}^{\neq} \prod_{(i,j) \in E(H)} {\textbf{1}} \bigl\{ \, (v_i,v_j) \in E(G)\, \bigr\},\end{equation}
where
![]() $\sum^{\neq}$
denotes the sum over distinct k-tuples
$\sum^{\neq}$
denotes the sum over distinct k-tuples
![]() $v_1,\ldots,v_k$
and
$v_1,\ldots,v_k$
and
![]() $\textbf{1} \{ \cdot \}$
is an indicator function. Notice that the subgraphs counted by
$\textbf{1} \{ \cdot \}$
is an indicator function. Notice that the subgraphs counted by
![]() ${\mathcal{C}}(H,G)$
are not necessarily induced subgraphs in G isomorphic to H. By (8), it is easy to derive a monotonicity property: if
${\mathcal{C}}(H,G)$
are not necessarily induced subgraphs in G isomorphic to H. By (8), it is easy to derive a monotonicity property: if
![]() $H_1,H_2$
are simple graphs on [k] such that
$H_1,H_2$
are simple graphs on [k] such that
![]() $E(H_1) \subset E(H_2)$
, then
$E(H_1) \subset E(H_2)$
, then
![]() ${\mathcal{C}}(H_2,G) \leq {\mathcal{C}}(H_1,G)$
.
${\mathcal{C}}(H_2,G) \leq {\mathcal{C}}(H_1,G)$
.
Let us return to our setup in Definition 1. If
![]() $N_n \geq k$
, we denote a collection of k-tuples of distinct elements in
$N_n \geq k$
, we denote a collection of k-tuples of distinct elements in
![]() $\mathcal{P}_n$
by
$\mathcal{P}_n$
by
Set
![]() $\mathcal P_{n,\neq}^k = \emptyset$
if
$\mathcal P_{n,\neq}^k = \emptyset$
if
![]() $N_n < k$
. Define the annulus
$N_n < k$
. Define the annulus
![]() $D_\gamma(R_n) \,{:\!=}\, B(0,R_n){\setminus}\mathring{B}(0, (1-\gamma)R_n)$
for
$D_\gamma(R_n) \,{:\!=}\, B(0,R_n){\setminus}\mathring{B}(0, (1-\gamma)R_n)$
for
![]() $0 < \gamma \leq 1$
, where
$0 < \gamma \leq 1$
, where
![]() $\mathring{A}$
denotes the interior of a set A. Constructing the hyperbolic random geometric graph on
$\mathring{A}$
denotes the interior of a set A. Constructing the hyperbolic random geometric graph on
![]() $\mathcal{P}_n \cap D_\gamma(R_n)$
as in Definition 1, we denote it by
$\mathcal{P}_n \cap D_\gamma(R_n)$
as in Definition 1, we denote it by
![]() $HG_n^{(\gamma)}(R_n ;\ \alpha, \zeta)$
. For
$HG_n^{(\gamma)}(R_n ;\ \alpha, \zeta)$
. For
![]() $k\ge 2$
, let
$k\ge 2$
, let
![]() $\Gamma_k$
be a tree with nodes [k] and edge set E. Our interest lies in the sub-tree counts
$\Gamma_k$
be a tree with nodes [k] and edge set E. Our interest lies in the sub-tree counts
![]() $S_n^{(\gamma)} \,{:\!=}\, {\mathcal{C}}\bigl(\Gamma_k,HG^{(\gamma)}_n(R_n;\ \alpha, \zeta)\bigr)$
for
$S_n^{(\gamma)} \,{:\!=}\, {\mathcal{C}}\bigl(\Gamma_k,HG^{(\gamma)}_n(R_n;\ \alpha, \zeta)\bigr)$
for
![]() $\gamma \in (0,1]$
. Recalling that
$\gamma \in (0,1]$
. Recalling that
![]() $T_i = R_n-d_\zeta(0,X_i)$
and using (8), one can represent
$T_i = R_n-d_\zeta(0,X_i)$
and using (8), one can represent
![]() $S_n^{(\gamma)}$
as
$S_n^{(\gamma)}$
as
In particular, we write
![]() $S_n \,{:\!=}\, S_n^{(1)}$
. Then
$S_n \,{:\!=}\, S_n^{(1)}$
. Then
![]() $S_n = {\mathcal{C}}\bigl(\Gamma_k,HG_n(R_n;\ \alpha, \zeta)\bigr)$
. Our first result gives the asymptotic growth rate of
$S_n = {\mathcal{C}}\bigl(\Gamma_k,HG_n(R_n;\ \alpha, \zeta)\bigr)$
. Our first result gives the asymptotic growth rate of
![]() $\mathbb{E}(S_n^{(\gamma)})$
for
$\mathbb{E}(S_n^{(\gamma)})$
for
![]() $\gamma \in (0,1]$
.
$\gamma \in (0,1]$
.
Theorem 1. Let
![]() $\Gamma_k$
be a tree on k vertices (
$\Gamma_k$
be a tree on k vertices (
![]() $k \geq 2$
) with degree sequence
$k \geq 2$
) with degree sequence
![]() $d_1,\ldots,d_k$
, and let
$d_1,\ldots,d_k$
, and let
![]() $S_n^{(\gamma)}$
be the sub-tree counts in (10). For
$S_n^{(\gamma)}$
be the sub-tree counts in (10). For
![]() $ \gamma \in (0,1) \setminus \{\frac{1}{2}\}$
, we have
$ \gamma \in (0,1) \setminus \{\frac{1}{2}\}$
, we have
 \begin{equation} \mathbb{E} \Big( S_n^{(\gamma)} \Big) \sim \bigg( \frac{2^{d-1}}{\kappa_{d-2}}\bigg)^{k-1} \alpha^k (d-1) \, n^k e^{-\zeta (d-1) (k-1) R_n/2} \prod_{i=1}^k a_n^{(\gamma)}(d_i), \ \ n\to\infty,\end{equation}
\begin{equation} \mathbb{E} \Big( S_n^{(\gamma)} \Big) \sim \bigg( \frac{2^{d-1}}{\kappa_{d-2}}\bigg)^{k-1} \alpha^k (d-1) \, n^k e^{-\zeta (d-1) (k-1) R_n/2} \prod_{i=1}^k a_n^{(\gamma)}(d_i), \ \ n\to\infty,\end{equation}
where
For
![]() $\gamma = 1/2$
, we have
$\gamma = 1/2$
, we have
 \begin{equation} \mathbb{E} \bigl( S_n^{(\gamma)} \bigr) = \Theta(n^k e^{-\zeta (d-1) (k-1) R_n/2} \prod_{i=1}^k a_n^{(1/2)}(d_i)), \ \ n\to\infty.\end{equation}
\begin{equation} \mathbb{E} \bigl( S_n^{(\gamma)} \bigr) = \Theta(n^k e^{-\zeta (d-1) (k-1) R_n/2} \prod_{i=1}^k a_n^{(1/2)}(d_i)), \ \ n\to\infty.\end{equation}
Furthermore, let
![]() $d_{(1)} \leq d_{(2)} \leq \ldots \leq d_{(k)}$
be the degree sequence of
$d_{(1)} \leq d_{(2)} \leq \ldots \leq d_{(k)}$
be the degree sequence of
![]() $\Gamma_k$
arranged in ascending order. If
$\Gamma_k$
arranged in ascending order. If
![]() $2\alpha /\zeta > d_{(k)}$
, then, for all
$2\alpha /\zeta > d_{(k)}$
, then, for all
![]() $\gamma \in (0,1]$
, we have
$\gamma \in (0,1]$
, we have
 \begin{align}\mathbb{E} ( S_n ) & \sim \mathbb{E} (S_n^{(\gamma)}) \sim \Bigg( \frac{2^{d-1}}{(d-1)\kappa_{d-2}} \Bigg)^{k-1} \alpha^k \, \prod_{i=1}^k \bigg( \alpha -\frac{\zeta d_i}{2}\bigg)^{-1} n^k e^{-\zeta (d-1) (k-1)R_n/2}, \ \ n\to\infty. \end{align}
\begin{align}\mathbb{E} ( S_n ) & \sim \mathbb{E} (S_n^{(\gamma)}) \sim \Bigg( \frac{2^{d-1}}{(d-1)\kappa_{d-2}} \Bigg)^{k-1} \alpha^k \, \prod_{i=1}^k \bigg( \alpha -\frac{\zeta d_i}{2}\bigg)^{-1} n^k e^{-\zeta (d-1) (k-1)R_n/2}, \ \ n\to\infty. \end{align}
Remark 1. Many of the previous studies cited in Section 1.2 set either
![]() $\alpha$
or
$\alpha$
or
![]() $\zeta$
to be 1, because in their setup, the asymptotics of the hyperbolic random geometric graph is completely determined by the ratio
$\zeta$
to be 1, because in their setup, the asymptotics of the hyperbolic random geometric graph is completely determined by the ratio
![]() $\alpha /\zeta$
. The crucial assumption in these studies is
$\alpha /\zeta$
. The crucial assumption in these studies is
for some positive constant
![]() $\nu$
. In the current study, however, we do not put any stringent assumptions on
$\nu$
. In the current study, however, we do not put any stringent assumptions on
![]() $R_n$
as in (14). Consequently, as seen in (11)–(13),
$R_n$
as in (14). Consequently, as seen in (11)–(13),
![]() $\zeta$
contributes, as an individual parameter, to the asymptotics of sub-tree counts via the term
$\zeta$
contributes, as an individual parameter, to the asymptotics of sub-tree counts via the term
![]() $e^{-\zeta (d-1) (k-1) R_n/2}$
.
$e^{-\zeta (d-1) (k-1) R_n/2}$
.
Theorem 1 indicates that the asymptotics of
![]() $\mathbb{E} \big( S_n^{(\gamma)} \big)$
are crucially determined by the underlying curvatures
$\mathbb{E} \big( S_n^{(\gamma)} \big)$
are crucially determined by the underlying curvatures
![]() $-\zeta^2$
and
$-\zeta^2$
and
![]() $-\alpha^2$
. To make the implication of the theorem more transparent, we fix
$-\alpha^2$
. To make the implication of the theorem more transparent, we fix
![]() $\zeta$
and think of
$\zeta$
and think of
![]() $\alpha$
as a parameter. If
$\alpha$
as a parameter. If
![]() $\alpha >0$
is sufficiently large, i.e., the space
$\alpha >0$
is sufficiently large, i.e., the space
![]() $B_d^{(\alpha)}$
is sufficiently hyperbolic, sub-trees are asymptotically dominated by the contributions near the boundary of
$B_d^{(\alpha)}$
is sufficiently hyperbolic, sub-trees are asymptotically dominated by the contributions near the boundary of
![]() $B(0,R_n)$
. More specifically, if
$B(0,R_n)$
. More specifically, if
![]() $2\alpha /\zeta > d_{(k)}$
, then
$2\alpha /\zeta > d_{(k)}$
, then
![]() $a_n^{(\gamma)} (d_i)$
,
$a_n^{(\gamma)} (d_i)$
,
![]() $i=1,\dots,k$
, all converge to a positive constant, and thus the growth rate of
$i=1,\dots,k$
, all converge to a positive constant, and thus the growth rate of
![]() $\mathbb{E} \big( S_n^{(\gamma)} \big)$
does not depend on
$\mathbb{E} \big( S_n^{(\gamma)} \big)$
does not depend on
![]() $\gamma$
, implying that the spatial distribution of sub-trees is completely determined by those near the boundary of
$\gamma$
, implying that the spatial distribution of sub-trees is completely determined by those near the boundary of
![]() $B(0,R_n)$
. In fact, for each
$B(0,R_n)$
. In fact, for each
![]() $\gamma \in (0,1)$
, the growth rate of
$\gamma \in (0,1)$
, the growth rate of
![]() $\mathbb{E} \big( S_n^{(\gamma)} \big)$
coincides with that of
$\mathbb{E} \big( S_n^{(\gamma)} \big)$
coincides with that of
![]() $\mathbb{E}( S_n )$
.
$\mathbb{E}( S_n )$
.
On the other hand, if
![]() $\alpha$
becomes smaller, i.e., the space
$\alpha$
becomes smaller, i.e., the space
![]() $B_d^{(\alpha)}$
becomes flatter, then the spatial distribution of sub-trees begins to be affected by those scattered away from the boundary of
$B_d^{(\alpha)}$
becomes flatter, then the spatial distribution of sub-trees begins to be affected by those scattered away from the boundary of
![]() $B(0,R_n)$
. For example, if
$B(0,R_n)$
. For example, if
![]() $d_{(k-1)} < 2\alpha /\zeta < d_{(k)} $
, we see that as
$d_{(k-1)} < 2\alpha /\zeta < d_{(k)} $
, we see that as
![]() $n \to \infty$
,
$n \to \infty$
,
while
![]() $a_n^{(\gamma)} (d_{(i)})$
,
$a_n^{(\gamma)} (d_{(i)})$
,
![]() $i=1,\dots,k-1$
, all tend to a positive constant. In this case, the growth rate of
$i=1,\dots,k-1$
, all tend to a positive constant. In this case, the growth rate of
![]() $\mathbb{E}\big( S_n^{(\gamma)} \big)$
is no longer independent of
$\mathbb{E}\big( S_n^{(\gamma)} \big)$
is no longer independent of
![]() $\gamma$
, and the growth rate becomes faster as
$\gamma$
, and the growth rate becomes faster as
![]() $\gamma \nearrow 1$
, i.e., as the inner radius of the corresponding annulus shrinks. Moreover, if
$\gamma \nearrow 1$
, i.e., as the inner radius of the corresponding annulus shrinks. Moreover, if
![]() $\alpha$
becomes even smaller, so that
$\alpha$
becomes even smaller, so that
![]() $d_{(k-2)}< 2\alpha/\zeta < d_{(k-1)}$
, then
$d_{(k-2)}< 2\alpha/\zeta < d_{(k-1)}$
, then
![]() $a_n^{(\gamma)} (d_{(k-1)})$
also asymptotically contributes to the growth rate of
$a_n^{(\gamma)} (d_{(k-1)})$
also asymptotically contributes to the growth rate of
![]() $\mathbb{E} \big( S_n^{(\gamma)} \big)$
. Finally, if
$\mathbb{E} \big( S_n^{(\gamma)} \big)$
. Finally, if
![]() $0 < 2\alpha /\zeta < d_{(1)}$
, then all of the terms
$0 < 2\alpha /\zeta < d_{(1)}$
, then all of the terms
![]() $a_n^{(\gamma)} (d_i)$
contribute to the growth rate of
$a_n^{(\gamma)} (d_i)$
contribute to the growth rate of
![]() $\mathbb{E} \big( S_n^{(\gamma)} \big)$
.
$\mathbb{E} \big( S_n^{(\gamma)} \big)$
.
The corollary below claims that if an underlying tree
![]() $\Gamma_k$
is a k-star such that
$\Gamma_k$
is a k-star such that
![]() $d_{(k)} = k-1$
,
$d_{(k)} = k-1$
,
![]() $d_{(k-1)} = \cdots =d_{(1)} =1$
, then even more can be said about the asymptotics of
$d_{(k-1)} = \cdots =d_{(1)} =1$
, then even more can be said about the asymptotics of
![]() $\log \mathbb{E}( S_n)$
.
$\log \mathbb{E}( S_n)$
.
Corollary 1. Let
![]() $\Gamma_k$
be a k-star with
$\Gamma_k$
be a k-star with
![]() $k\ge2$
. Moreover, assume that
$k\ge2$
. Moreover, assume that
![]() $R_n$
satisfies
$R_n$
satisfies
(note that
![]() $c=0$
or
$c=0$
or
![]() $c=\infty$
is possible). Let
$c=\infty$
is possible). Let
![]() $a \vee b = \max \{a,b \}$
for
$a \vee b = \max \{a,b \}$
for
![]() $a,b\in {\mathbb R}$
.
$a,b\in {\mathbb R}$
.
-
(i) If
 $2\alpha /\zeta > k-1$
, (15)
$2\alpha /\zeta > k-1$
, (15) \begin{align}\mathbb{E} ( S_n) \sim \bigg( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\bigg)^{k-1} & \alpha^k \, \bigl( \alpha -\zeta(k-1)/2\bigr)^{-1} \nonumber\\[3pt]&\times \bigl( \alpha - \zeta/2 \bigr)^{-(k-1)} n^k e^{- \zeta (d-1)(k-1)R_n/2}, \ \ \ n\to\infty. \end{align}
\begin{align}\mathbb{E} ( S_n) \sim \bigg( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\bigg)^{k-1} & \alpha^k \, \bigl( \alpha -\zeta(k-1)/2\bigr)^{-1} \nonumber\\[3pt]&\times \bigl( \alpha - \zeta/2 \bigr)^{-(k-1)} n^k e^{- \zeta (d-1)(k-1)R_n/2}, \ \ \ n\to\infty. \end{align}
-
(ii) If
 $1 < 2\alpha/\zeta \leq k-1$
,
$1 < 2\alpha/\zeta \leq k-1$
,  \begin{align*}\frac{\log \mathbb{E}(S_n )}{R_n \vee \log n} \to k(c\vee 1)^{-1} - \alpha(d-1 ) \big(1\vee c^{-1}\big)^{-1}, \ \ \ n\to\infty.\end{align*}
\begin{align*}\frac{\log \mathbb{E}(S_n )}{R_n \vee \log n} \to k(c\vee 1)^{-1} - \alpha(d-1 ) \big(1\vee c^{-1}\big)^{-1}, \ \ \ n\to\infty.\end{align*}
-
(iii) If
 $0 < 2\alpha /\zeta \leq 1$
,
$0 < 2\alpha /\zeta \leq 1$
,  \begin{align*}\frac{\log \mathbb{E}(S_n )}{R_n\vee\log n} \to k(c\vee 1)^{-1}-(d-1)\bigl( \alpha k- \zeta(k-1)/2 \bigl) \big(1\vee c^{-1}\big)^{-1}, \ \ \ n\to\infty.\end{align*}
\begin{align*}\frac{\log \mathbb{E}(S_n )}{R_n\vee\log n} \to k(c\vee 1)^{-1}-(d-1)\bigl( \alpha k- \zeta(k-1)/2 \bigl) \big(1\vee c^{-1}\big)^{-1}, \ \ \ n\to\infty.\end{align*}
Our ultimate goal is to establish the CLT for the sub-tree counts
![]() $S_n^{(\gamma)}$
for
$S_n^{(\gamma)}$
for
![]() $0 <\gamma \leq 1$
. Before describing it, however, it is important to investigate the variance asymptotics. The theorem below provides an asymptotic lower bound for
$0 <\gamma \leq 1$
. Before describing it, however, it is important to investigate the variance asymptotics. The theorem below provides an asymptotic lower bound for
![]() $\mathbb{V}ar(S_n^{(\gamma)})$
up to a constant factor. Similarly to Theorem 1, if
$\mathbb{V}ar(S_n^{(\gamma)})$
up to a constant factor. Similarly to Theorem 1, if
![]() $\alpha /\zeta > d_{(k)}$
, the lower bound of
$\alpha /\zeta > d_{(k)}$
, the lower bound of
![]() $\mathbb{V}ar(S_n^{(\gamma)})$
is independent of
$\mathbb{V}ar(S_n^{(\gamma)})$
is independent of
![]() $\gamma$
, whereas it depends on
$\gamma$
, whereas it depends on
![]() $\gamma$
when
$\gamma$
when
![]() $\alpha /\zeta \leq d_{(k)}$
. Furthermore, if
$\alpha /\zeta \leq d_{(k)}$
. Furthermore, if
![]() $\alpha /\zeta > d_{(k)}$
, we can obtain the exact growth rate of
$\alpha /\zeta > d_{(k)}$
, we can obtain the exact growth rate of
![]() $\mathbb{V}ar(S_n)$
. For two sequences
$\mathbb{V}ar(S_n)$
. For two sequences
![]() $(a_n)$
and
$(a_n)$
and
![]() $(b_n)$
, we write
$(b_n)$
, we write
![]() $a_n=\Omega(b_n)$
if there exists a positive constant C such that
$a_n=\Omega(b_n)$
if there exists a positive constant C such that
![]() $a_n/b_n\ge C$
for all
$a_n/b_n\ge C$
for all
![]() $n\ge1$
. Furthermore,
$n\ge1$
. Furthermore,
![]() $C^*$
denotes a generic positive constant, which may vary between lines and does not depend on n.
$C^*$
denotes a generic positive constant, which may vary between lines and does not depend on n.
Theorem 2. Let
![]() $\Gamma_k$
be a tree on k vertices (
$\Gamma_k$
be a tree on k vertices (
![]() $k \geq 2$
) with degree sequence
$k \geq 2$
) with degree sequence
![]() $d_1,\ldots,d_k$
, and let
$d_1,\ldots,d_k$
, and let
![]() $S_n^{(\gamma)}$
be the sub-tree counts in (10). For
$S_n^{(\gamma)}$
be the sub-tree counts in (10). For
![]() $0 < \gamma <1$
,
$0 < \gamma <1$
,
 \begin{align}\mathbb{V}ar(S_n^{(\gamma)}) &= \Omega \biggl( n^{2k-1}e^{-\zeta(d-1)(k-1)R_n} a_n^{(\gamma)}(2d_{(k)})\, \prod_{i=1}^{k-1} a_n^{(\gamma)} (d_{(i)})^2\, \notag \\[3pt] &\qquad \qquad \qquad \qquad \qquad \qquad \qquad \vee \, n^k e^{-\zeta(d-1) (k-1)R_n/2} \prod_{i=1}^k a_n^{(\gamma)} (d_i) \biggr). \end{align}
\begin{align}\mathbb{V}ar(S_n^{(\gamma)}) &= \Omega \biggl( n^{2k-1}e^{-\zeta(d-1)(k-1)R_n} a_n^{(\gamma)}(2d_{(k)})\, \prod_{i=1}^{k-1} a_n^{(\gamma)} (d_{(i)})^2\, \notag \\[3pt] &\qquad \qquad \qquad \qquad \qquad \qquad \qquad \vee \, n^k e^{-\zeta(d-1) (k-1)R_n/2} \prod_{i=1}^k a_n^{(\gamma)} (d_i) \biggr). \end{align}
Suppose further that
![]() $\alpha /\zeta > d_{(k)}$
; then, for all
$\alpha /\zeta > d_{(k)}$
; then, for all
![]() $\gamma \in (0,1]$
, we have
$\gamma \in (0,1]$
, we have
The main point of (17) is that the growth rate of
![]() $\mathbb{V}ar(S_n)$
is determined by how rapidly
$\mathbb{V}ar(S_n)$
is determined by how rapidly
![]() $R_n$
grows to infinity. To see this in more detail, we consider a special case for which
$R_n$
grows to infinity. To see this in more detail, we consider a special case for which
![]() $R_n = c \log n$
for some
$R_n = c \log n$
for some
![]() $c \in (0,\infty)$
. Then we can observe the following phase transitions:
$c \in (0,\infty)$
. Then we can observe the following phase transitions:
 \begin{equation*}\mathbb{V}ar(S_n) \sim\begin{cases} C^* n^{2k-1 - c\zeta(d-1) (k-1)} & \text{if} \, \, 0 < c < 2 \zeta^{-1}(d-1)^{-1}, \\ \\[-9pt] C^* n & \text{if} \, \, c=2 \zeta^{-1} (d-1)^{-1},\\ \\[-9pt]C^* n^{k - c\zeta (d-1)(k-1)/2} & \text{if} \, \, c > 2 \zeta^{-1}(d-1)^{-1}.\end{cases}\end{equation*}
\begin{equation*}\mathbb{V}ar(S_n) \sim\begin{cases} C^* n^{2k-1 - c\zeta(d-1) (k-1)} & \text{if} \, \, 0 < c < 2 \zeta^{-1}(d-1)^{-1}, \\ \\[-9pt] C^* n & \text{if} \, \, c=2 \zeta^{-1} (d-1)^{-1},\\ \\[-9pt]C^* n^{k - c\zeta (d-1)(k-1)/2} & \text{if} \, \, c > 2 \zeta^{-1}(d-1)^{-1}.\end{cases}\end{equation*}
Moreover, Theorems 1 and 2 imply that, in the case of
![]() $ \alpha/\zeta < d_{(k)} < 2\alpha /\zeta$
,
$ \alpha/\zeta < d_{(k)} < 2\alpha /\zeta$
,
![]() $\mathbb{V}ar(S_n^{(\gamma)})$
grows super-linearly, while the expectation exhibits only linear growth. A similar phenomenon has been observed for isolated points in [Reference Fountoulakis and Yukich23, Theorem 1.1]. This is indicative of a power-law behaviour in the sub-tree counts.
$\mathbb{V}ar(S_n^{(\gamma)})$
grows super-linearly, while the expectation exhibits only linear growth. A similar phenomenon has been observed for isolated points in [Reference Fountoulakis and Yukich23, Theorem 1.1]. This is indicative of a power-law behaviour in the sub-tree counts.
2.3. Central limit theorem for sub-tree counts
Having derived variance bounds, we proceed to prove the CLT for
![]() $S_n^{(\gamma)}$
. Before stating the normal approximation result, we need to define the two metrics to be used: the Wasserstein distance
$S_n^{(\gamma)}$
. Before stating the normal approximation result, we need to define the two metrics to be used: the Wasserstein distance
![]() $d_W$
and the Kolmogorov distance
$d_W$
and the Kolmogorov distance
![]() $d_K$
. Let
$d_K$
. Let
![]() $Y_1,Y_2$
be two random variables, and let Lip(1) be the set of Lipschitz functions
$Y_1,Y_2$
be two random variables, and let Lip(1) be the set of Lipschitz functions
![]() $h \,{:}\, {\mathbb R} \to {\mathbb R}$
with Lipschitz constant of at most 1. Then we define the two metrics as follows:
$h \,{:}\, {\mathbb R} \to {\mathbb R}$
with Lipschitz constant of at most 1. Then we define the two metrics as follows:
 \begin{eqnarray*}d_W(Y_1,Y_2) & = & \sup_{h \in Lip(1)}\bigl|\, \mathbb{E}\bigl(h(Y_1)\bigr) - \mathbb{E}\bigl(h(Y_2)\bigr)\, \bigr|, \\[3pt] d_K(Y_1,Y_2) & = & \sup_{x \in {\mathbb R}}\, \bigl|\, \mathbb{P}(Y_1 \leq x) - \mathbb{P}(Y_2 \leq x)\, \bigr|. \nonumber\end{eqnarray*}
\begin{eqnarray*}d_W(Y_1,Y_2) & = & \sup_{h \in Lip(1)}\bigl|\, \mathbb{E}\bigl(h(Y_1)\bigr) - \mathbb{E}\bigl(h(Y_2)\bigr)\, \bigr|, \\[3pt] d_K(Y_1,Y_2) & = & \sup_{x \in {\mathbb R}}\, \bigl|\, \mathbb{P}(Y_1 \leq x) - \mathbb{P}(Y_2 \leq x)\, \bigr|. \nonumber\end{eqnarray*}
Although we have defined
![]() $d_W, d_K$
as distances between two random variables, they are actually distances between two probability distributions. Let N denote the standard normal random variable, and let
$d_W, d_K$
as distances between two random variables, they are actually distances between two probability distributions. Let N denote the standard normal random variable, and let
![]() $\Rightarrow$
denote weak convergence in
$\Rightarrow$
denote weak convergence in
![]() ${\mathbb R}$
. In our proof, we derive more detailed, albeit complicated, bounds that indicate the scope for improvement.
${\mathbb R}$
. In our proof, we derive more detailed, albeit complicated, bounds that indicate the scope for improvement.
Theorem 3. Let
![]() $\Gamma_k$
be a tree on k vertices (
$\Gamma_k$
be a tree on k vertices (
![]() $k \geq 2$
) with degree sequence
$k \geq 2$
) with degree sequence
![]() $d_1,\ldots,d_k$
, and let
$d_1,\ldots,d_k$
, and let
![]() $S_n^{(\gamma)}$
be the sub-tree counts in (10). Assume further that
$S_n^{(\gamma)}$
be the sub-tree counts in (10). Assume further that
![]() $R_n$
satisfies
$R_n$
satisfies
For every
![]() $0 < a < 1/2$
, there exists
$0 < a < 1/2$
, there exists
![]() $0 < \gamma_0 < 1/2$
such that for all
$0 < \gamma_0 < 1/2$
such that for all
![]() $0 < \gamma < \gamma_0$
, we have
$0 < \gamma < \gamma_0$
, we have
 \begin{equation}d_W\left( \frac{S_n^{(\gamma)} - \mathbb{E}(S_n^{(\gamma)})}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) = O(n^{-a}), \, \, \, \, d_K\left( \frac{S_n^{(\gamma)} - \mathbb{E}(S_n^{(\gamma)})}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) = O(n^{-a}).\end{equation}
\begin{equation}d_W\left( \frac{S_n^{(\gamma)} - \mathbb{E}(S_n^{(\gamma)})}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) = O(n^{-a}), \, \, \, \, d_K\left( \frac{S_n^{(\gamma)} - \mathbb{E}(S_n^{(\gamma)})}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) = O(n^{-a}).\end{equation}
Furthermore, if
![]() $\alpha /\zeta > d_{(k)}$
, then
$\alpha /\zeta > d_{(k)}$
, then
Here, we claim that for a small enough
![]() $\gamma$
, the CLT holds for
$\gamma$
, the CLT holds for
![]() $S_n^{(\gamma)}$
, and if
$S_n^{(\gamma)}$
, and if
![]() $\alpha / \zeta > d_{(k)}$
, the CLT holds for
$\alpha / \zeta > d_{(k)}$
, the CLT holds for
![]() $S_n$
as well. Heuristically, a larger
$S_n$
as well. Heuristically, a larger
![]() $\alpha / \zeta$
means that the space
$\alpha / \zeta$
means that the space
![]() $B_d^{(\alpha)}$
is more hyperbolic relative to
$B_d^{(\alpha)}$
is more hyperbolic relative to
![]() $B_d^{(\zeta)}$
and hence contains more points in the boundary. So in that case,
$B_d^{(\zeta)}$
and hence contains more points in the boundary. So in that case,
![]() $S_n$
is well approximated by
$S_n$
is well approximated by
![]() $S_n^{(\gamma)}$
. Note that the CLT for
$S_n^{(\gamma)}$
. Note that the CLT for
![]() $S_n^{(\gamma)}$
possibly holds even when the variance grows super-linearly in n. It is still unclear whether or not the CLT holds for
$S_n^{(\gamma)}$
possibly holds even when the variance grows super-linearly in n. It is still unclear whether or not the CLT holds for
![]() $S_n$
under super-linear growth of the variance. In [Reference Fountoulakis and Yukich23, Theorem 1.3], it is shown that the CLT for ‘isolated points’ cannot hold under super-linear growth of the variance. Finally, Remark 4 at the end of Section 3.3.3 gives a more precise quantification of the bounds in (19).
$S_n$
under super-linear growth of the variance. In [Reference Fountoulakis and Yukich23, Theorem 1.3], it is shown that the CLT for ‘isolated points’ cannot hold under super-linear growth of the variance. Finally, Remark 4 at the end of Section 3.3.3 gives a more precise quantification of the bounds in (19).
Remark 2. If the constant c in (18) is finite and
![]() $2\alpha /\zeta>d_{(k)}$
, we see from (13) that
$2\alpha /\zeta>d_{(k)}$
, we see from (13) that
![]() $\mathbb{E}(S_n)$
is asymptotically equal to n, up to constant factors. This implies that
$\mathbb{E}(S_n)$
is asymptotically equal to n, up to constant factors. This implies that
![]() $S_n$
behaves similarly to the subgraph counts in the thermodynamic regime of the Euclidean setting (more detailed arguments on this point are given in Section 2.5). If
$S_n$
behaves similarly to the subgraph counts in the thermodynamic regime of the Euclidean setting (more detailed arguments on this point are given in Section 2.5). If
![]() $c=\infty$
in (18),
$c=\infty$
in (18),
![]() $R_n$
grows more slowly, so that the spatial distribution of
$R_n$
grows more slowly, so that the spatial distribution of
![]() $\Gamma_k$
becomes denser. For the sparse phase asymptotics, the first author’s ongoing work studies the case in which
$\Gamma_k$
becomes denser. For the sparse phase asymptotics, the first author’s ongoing work studies the case in which
![]() $R_n$
diverges faster than (18), so that
$R_n$
diverges faster than (18), so that
![]() $\mathbb{E}( S_n )$
is asymptotically equal to a positive constant. In this case, the tree-like structure rarely occurs, and
$\mathbb{E}( S_n )$
is asymptotically equal to a positive constant. In this case, the tree-like structure rarely occurs, and
![]() $S_n$
will be approximated by a Poisson random variable.
$S_n$
will be approximated by a Poisson random variable.
2.4. Special case and comparison with previous studies
The objective of this section is to restate our results in the special case
for some positive constant
![]() $\nu \in (0,\infty)$
. By doing so, we can make an easy comparison with previous studies. As mentioned before, most earlier works (e.g. [Reference Bode, Fountoulakis and Müller10, Reference Fountoulakis and Müller22, Reference Kiwi and Mitsche29, Reference Bode, Fountoulakis and Müller11, Reference Bläsius, Friedrich and Krohmer7, Reference Candellero and Fountoulakis14, Reference Gugelmann, Panagiotou and Peter25, Reference Candellero and Fountoulakis13, Reference Kiwi and Mitsche27, Reference Müller and Staps36, Reference Kiwi and Mitsche28, Reference Fountoulakis and Yukich23, Reference Abdullah, Bode and Fountoulakis1, Reference Fountoulakis19, Reference Fountoulakis20]) are concerned only with the case
$\nu \in (0,\infty)$
. By doing so, we can make an easy comparison with previous studies. As mentioned before, most earlier works (e.g. [Reference Bode, Fountoulakis and Müller10, Reference Fountoulakis and Müller22, Reference Kiwi and Mitsche29, Reference Bode, Fountoulakis and Müller11, Reference Bläsius, Friedrich and Krohmer7, Reference Candellero and Fountoulakis14, Reference Gugelmann, Panagiotou and Peter25, Reference Candellero and Fountoulakis13, Reference Kiwi and Mitsche27, Reference Müller and Staps36, Reference Kiwi and Mitsche28, Reference Fountoulakis and Yukich23, Reference Abdullah, Bode and Fountoulakis1, Reference Fountoulakis19, Reference Fountoulakis20]) are concerned only with the case
or its variants; hence, (21) serves as a higher-dimensional version of (22). Assuming (21) and
![]() $2\alpha / \zeta \notin {\mathbb N}$
, it is easy to see that as
$2\alpha / \zeta \notin {\mathbb N}$
, it is easy to see that as
![]() $n \to \infty$
,
$n \to \infty$
,
where
![]() $(a)_+ = a$
if
$(a)_+ = a$
if
![]() $a>0$
and
$a>0$
and
![]() $(a)_+=0$
otherwise.
$(a)_+=0$
otherwise.
Corollary 2. Let
![]() $R_n = 2[\zeta (d-1)]^{-1} \log (n/\nu)$
, let
$R_n = 2[\zeta (d-1)]^{-1} \log (n/\nu)$
, let
![]() $\Gamma_k$
be a tree on k vertices (
$\Gamma_k$
be a tree on k vertices (
![]() $k\geq 2$
) with degree sequence
$k\geq 2$
) with degree sequence
![]() $d_1,\dots,d_k$
, and let
$d_1,\dots,d_k$
, and let
![]() $S_n^{(\gamma)}$
be a sub-tree count as in (10). Suppose that
$S_n^{(\gamma)}$
be a sub-tree count as in (10). Suppose that
![]() $2\alpha /\zeta$
is not an integer. For
$2\alpha /\zeta$
is not an integer. For
![]() $\gamma \in (0,1) \setminus \{\frac{1}{2}\}$
, we have, as
$\gamma \in (0,1) \setminus \{\frac{1}{2}\}$
, we have, as
![]() $n\to\infty$
,
$n\to\infty$
,
 \begin{align*}\mathbb{E}(S_n^{(\gamma)}) \sim \biggl( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\biggr)^{k-1} \alpha^k &\prod_{j=1}^k\, \Bigl|\, \alpha - \frac{\zeta}{2} d_j \, \Bigr|^{-1} \nu^{k-1-\gamma \sum_{i=1}^k (d_i - 2\alpha /\zeta)_+} n^{1 + \gamma\sum_{i=1}^k (d_i - 2\alpha /\zeta)_+},\end{align*}
\begin{align*}\mathbb{E}(S_n^{(\gamma)}) \sim \biggl( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\biggr)^{k-1} \alpha^k &\prod_{j=1}^k\, \Bigl|\, \alpha - \frac{\zeta}{2} d_j \, \Bigr|^{-1} \nu^{k-1-\gamma \sum_{i=1}^k (d_i - 2\alpha /\zeta)_+} n^{1 + \gamma\sum_{i=1}^k (d_i - 2\alpha /\zeta)_+},\end{align*}
and for
![]() $\gamma = 1/2$
, we have
$\gamma = 1/2$
, we have
Furthermore, as for the variance asymptotics, we have for
![]() $\gamma \in (0,1)$
$\gamma \in (0,1)$
If
![]() $2\alpha /\zeta > d_{(k)}$
, we have for
$2\alpha /\zeta > d_{(k)}$
, we have for
![]() $\gamma \in (0,1]$
$\gamma \in (0,1]$
 \begin{equation} \mathbb{E} (S_n) \sim \mathbb{E}(S_n^{(\gamma)}) \sim \biggl( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\biggr)^{k-1} \alpha^k \prod_{j=1}^k\, \Bigl(\, \alpha - \frac{\zeta}{2} d_j \, \Bigr)^{-1} \nu^{k-1}n, \ \ \ n\to\infty.\end{equation}
\begin{equation} \mathbb{E} (S_n) \sim \mathbb{E}(S_n^{(\gamma)}) \sim \biggl( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\biggr)^{k-1} \alpha^k \prod_{j=1}^k\, \Bigl(\, \alpha - \frac{\zeta}{2} d_j \, \Bigr)^{-1} \nu^{k-1}n, \ \ \ n\to\infty.\end{equation}
If
![]() $\alpha / \zeta > d_{(k)}$
, we have for
$\alpha / \zeta > d_{(k)}$
, we have for
![]() $\gamma \in (0,1]$
$\gamma \in (0,1]$
To avoid repetition, we do not state the corresponding CLT. However, it holds under the assumptions of Corollary 2. Note that (24) is a partial generalization of [Reference Candellero and Fountoulakis14, Claim 5.2] to higher dimensions.
Now we compare the results in Corollary 2 with those in the existing literature. If we choose
![]() $k =2$
in (25), then
$k =2$
in (25), then
![]() $S_n$
represents the number of edges with
$S_n$
represents the number of edges with
![]() $d_{(2)}=1$
. Moreover,
$d_{(2)}=1$
. Moreover,
![]() $S_n/2n$
denotes the empirical degree distribution. Then (25) asserts that
$S_n/2n$
denotes the empirical degree distribution. Then (25) asserts that
![]() $\mathbb{E}(S_n/2n) \to C^*$
if
$\mathbb{E}(S_n/2n) \to C^*$
if
![]() $\alpha /\zeta > 1/2$
. The convergence of the expected typical degree to a constant indicates that this regime is, in nature, the thermodynamic regime. Furthermore, when
$\alpha /\zeta > 1/2$
. The convergence of the expected typical degree to a constant indicates that this regime is, in nature, the thermodynamic regime. Furthermore, when
![]() $1/2 < \alpha / \zeta < 1$
, the expected degree distribution converges to a constant, but the variance diverges. This is consistent with the power-law behaviour for degree distributions with exponent
$1/2 < \alpha / \zeta < 1$
, the expected degree distribution converges to a constant, but the variance diverges. This is consistent with the power-law behaviour for degree distributions with exponent
![]() $2\alpha /\zeta +1$
, which itself was predicted in [Reference Krioukov30]. Such a power-law behaviour for degree distributions was proven in [Reference Gugelmann, Panagiotou and Peter25, Reference Fountoulakis19] for
$2\alpha /\zeta +1$
, which itself was predicted in [Reference Krioukov30]. Such a power-law behaviour for degree distributions was proven in [Reference Gugelmann, Panagiotou and Peter25, Reference Fountoulakis19] for
![]() $d = 2$
. For
$d = 2$
. For
![]() $2\alpha /\zeta \leq 1$
, the expected average degree grows to infinity, which is again consistent with the conjecture that the degree distribution has a power-law behaviour with exponent 2 (see [Reference Krioukov30]).
$2\alpha /\zeta \leq 1$
, the expected average degree grows to infinity, which is again consistent with the conjecture that the degree distribution has a power-law behaviour with exponent 2 (see [Reference Krioukov30]).
In Table 1, we summarize some of the results in the existing literature and those in this paper in the case
![]() $d = 2$
,
$d = 2$
,
![]() $\zeta = 1$
,
$\zeta = 1$
,
![]() $R_n = 2 \log (n / \nu)$
,
$R_n = 2 \log (n / \nu)$
,
![]() $\nu \in (0,\infty)$
. As seen in Table 1, our results demonstrate various phase transitions. For example, for
$\nu \in (0,\infty)$
. As seen in Table 1, our results demonstrate various phase transitions. For example, for
![]() $1 < \alpha < d_{(k)}/2$
, the expected sub-tree counts grow super-linearly in n, whereas the expected number of k-cliques is linear, and there is no ‘giant component’. This justifies our observation in Section 1.2 that hyperbolic random geometric graphs contain many tree-like hierarchical structures, as compared to their Euclidean counterparts.
$1 < \alpha < d_{(k)}/2$
, the expected sub-tree counts grow super-linearly in n, whereas the expected number of k-cliques is linear, and there is no ‘giant component’. This justifies our observation in Section 1.2 that hyperbolic random geometric graphs contain many tree-like hierarchical structures, as compared to their Euclidean counterparts.
2.5. Comparison to subgraph counts of Euclidean random geometric graphs
In this section, we sketch asymptotic results for subgraph counts of analogous random geometric graph models in the Euclidean space. We claim that the behaviour of the subgraph counts of the Euclidean analogues is significantly different from that of the counts in the previous sections. For example, in contrast to Theorem 1, the growth rates for the subgraph counts in the Euclidean case do not depend on the degree sequence of the subgraph under consideration.
For simplicity, we restrict ourselves to the case
![]() $\alpha = \zeta = 1$
and
$\alpha = \zeta = 1$
and
![]() $R_n = 2(d-1)^{-1}\log(n/\nu)$
for some
$R_n = 2(d-1)^{-1}\log(n/\nu)$
for some
![]() $\nu > 0$
as in Section 2.4. Then, by Corollary 2, we have that
$\nu > 0$
as in Section 2.4. Then, by Corollary 2, we have that
![]() $\mathbb{E}(E_n) = \Theta(n)$
, where
$\mathbb{E}(E_n) = \Theta(n)$
, where
![]() $E_n$
denotes the number of edges in
$E_n$
denotes the number of edges in
![]() $HG_n(R_n;\ 1,1)$
. We now consider two possible Euclidean analogues in the setting of Corollary 2. One of them is defined by following the construction of
$HG_n(R_n;\ 1,1)$
. We now consider two possible Euclidean analogues in the setting of Corollary 2. One of them is defined by following the construction of
![]() $HG_n(R_n;\ 1,1)$
, and the other is defined to ensure that the expected degree is of the same order as
$HG_n(R_n;\ 1,1)$
, and the other is defined to ensure that the expected degree is of the same order as
![]() $HG_n(R_n;\ 1,1)$
. It is a moot point as to which is the right analogue, and hence we make comparisons to both. See Figure 3 for the simulations of these Euclidean graphs.
$HG_n(R_n;\ 1,1)$
. It is a moot point as to which is the right analogue, and hence we make comparisons to both. See Figure 3 for the simulations of these Euclidean graphs.

Figure 3. Simulations of
![]() $EG_{1,100}$
with
$EG_{1,100}$
with
![]() $\pi r^2_{100} = 100$
and
$\pi r^2_{100} = 100$
and
![]() $EG_{2,500}$
with
$EG_{2,500}$
with
![]() $\pi r^2_{500} = 500, s_{500} =1$
for
$\pi r^2_{500} = 500, s_{500} =1$
for
![]() $d = 2$
.
$d = 2$
.
The two analogues are constructed as follows:
-
1. Consider Poisson(n) points distributed uniformly in a sequence of growing Euclidean balls of radius
 $r_n\to \infty$
, and connect any two points within a distance of
$r_n\to \infty$
, and connect any two points within a distance of
 $r_n$
(this is the dense regime). We call this graph
$r_n$
(this is the dense regime). We call this graph
 $EG_{1,n}$
. It has been defined by mimicking the construction of
$EG_{1,n}$
. It has been defined by mimicking the construction of
 $HG_n(R_n ;\ 1,1)$
.
$HG_n(R_n ;\ 1,1)$
. -
2. Consider Poisson(n) points distributed uniformly in a sequence of Euclidean balls of radius
 $r_n$
, and connect points within a distance
$r_n$
, and connect points within a distance
 $s_n$
such that the expected number of edges grows linearly in n (this is the thermodynamic regime). We call this graph
$s_n$
such that the expected number of edges grows linearly in n (this is the thermodynamic regime). We call this graph
 $EG_{2,n}$
. The expected degree of this graph is of the same order as
$EG_{2,n}$
. The expected degree of this graph is of the same order as
 $HG_n(R_n ;\ 1,1)$
.
$HG_n(R_n ;\ 1,1)$
.
We now give a sketch of the calculations for the subgraph counts in the above two models, referring the reader to [Reference Penrose38, Chapter 3] for details. Denote by
![]() ${\mathcal{X}}_n$
the collection of Poisson(n) points distributed uniformly in
${\mathcal{X}}_n$
the collection of Poisson(n) points distributed uniformly in
![]() $B_{r_n}(0) \subset {\mathbb R}^d$
, where
$B_{r_n}(0) \subset {\mathbb R}^d$
, where
![]() $B_{r_n}(0)$
is the d-dimensional ball of radius
$B_{r_n}(0)$
is the d-dimensional ball of radius
![]() $r_n$
centred at the origin. Then
$r_n$
centred at the origin. Then
![]() $EG_n(r_n,s_n)$
denotes the graph with vertex set
$EG_n(r_n,s_n)$
denotes the graph with vertex set
![]() ${\mathcal{X}}_n$
and edges between
${\mathcal{X}}_n$
and edges between
![]() $X_i,X_j \in {\mathcal{X}}_n$
such that
$X_i,X_j \in {\mathcal{X}}_n$
such that
![]() $|X_i - X_j| \leq s_n$
, where
$|X_i - X_j| \leq s_n$
, where
![]() $|\cdot|$
is the Euclidean metric. In this notation,
$|\cdot|$
is the Euclidean metric. In this notation,
![]() $EG_{1,n} = EG_n(r_n,r_n)$
and
$EG_{1,n} = EG_n(r_n,r_n)$
and
![]() $EG_{2,n} = EG_n(r_n,s_n)$
, where
$EG_{2,n} = EG_n(r_n,s_n)$
, where
![]() $s_n$
is chosen such that the expected number of edges grows linearly in n. Let
$s_n$
is chosen such that the expected number of edges grows linearly in n. Let
![]() $\Gamma$
be a connected graph on k vertices, and let
$\Gamma$
be a connected graph on k vertices, and let
![]() $J_{i,n}(\Gamma)$
,
$J_{i,n}(\Gamma)$
,
![]() $i=1,2$
, denote the number of copies of
$i=1,2$
, denote the number of copies of
![]() $\Gamma$
in
$\Gamma$
in
![]() $EG_{i,n}$
,
$EG_{i,n}$
,
![]() $i=1,2$
. By the Mecke formula, we have that
$i=1,2$
. By the Mecke formula, we have that
Since the order of
![]() $\mathbb{E}(J_{1,n}(\Gamma))$
is the same as that of the complete subgraph on
$\mathbb{E}(J_{1,n}(\Gamma))$
is the same as that of the complete subgraph on
![]() ${\mathcal{X}}_n$
, we call it the dense regime. We observe that the choice of
${\mathcal{X}}_n$
, we call it the dense regime. We observe that the choice of
![]() $r_n$
and the degree sequence of
$r_n$
and the degree sequence of
![]() $\Gamma$
do not contribute to the growth rate of
$\Gamma$
do not contribute to the growth rate of
![]() $\mathbb{E}(J_{1,n}(\Gamma))$
. This shows a striking contrast to the asymptotics for hyperbolic random geometric graphs in Corollary 2.
$\mathbb{E}(J_{1,n}(\Gamma))$
. This shows a striking contrast to the asymptotics for hyperbolic random geometric graphs in Corollary 2.
As in the above case, assuming
![]() $s_n = o(r_n)$
, we can also derive that
$s_n = o(r_n)$
, we can also derive that
![]() $\mathbb{E}(J_{2,n}(\Gamma)) = \Theta\bigl(n^k (\frac{s_n}{r_n})^{d(k-1)}\bigr)$
. In the special case of
$\mathbb{E}(J_{2,n}(\Gamma)) = \Theta\bigl(n^k (\frac{s_n}{r_n})^{d(k-1)}\bigr)$
. In the special case of
![]() $k=2$
and
$k=2$
and
![]() $s_n= n^{-1/d}r_n$
, this implies that the expected number of edges is asymptotically equal to n, up to a constant factor. The resulting regime is called the thermodynamic regime (see [Reference Penrose38, Chapter 3]), since the expected average degree (or empirical count of neighbours) is asymptotically constant. In contrast to the hyperbolic random geometric graph, the above calculation indicates that the asymptotics of
$s_n= n^{-1/d}r_n$
, this implies that the expected number of edges is asymptotically equal to n, up to a constant factor. The resulting regime is called the thermodynamic regime (see [Reference Penrose38, Chapter 3]), since the expected average degree (or empirical count of neighbours) is asymptotically constant. In contrast to the hyperbolic random geometric graph, the above calculation indicates that the asymptotics of
![]() $\mathbb{E}(J_{2,n}(\Gamma))$
is again independent of the degree sequence of
$\mathbb{E}(J_{2,n}(\Gamma))$
is again independent of the degree sequence of
![]() $\Gamma$
and the choice of
$\Gamma$
and the choice of
![]() $r_n$
. Finally, we wish to emphasize that the broad message remains unchanged even for the second-order results; see [Reference Penrose and Yukich39, Reference Bobrowski and Mukherjee8] for more detailed computations.
$r_n$
. Finally, we wish to emphasize that the broad message remains unchanged even for the second-order results; see [Reference Penrose and Yukich39, Reference Bobrowski and Mukherjee8] for more detailed computations.
3. Proofs
We first prove the basic lemma on an approximation of the hyperbolic probability density. Subsequently, Section 3.1 presents a few more lemmas concerned with hyperbolic distance. Utilizing these lemmas, we prove expectation and variance results for the sub-tree counts in Section 3.2. Finally, Section 3.3 establishes the required CLT. Throughout this section,
![]() $C^*$
denotes a generic positive constant, which may vary between lines and does not depend on n.
$C^*$
denotes a generic positive constant, which may vary between lines and does not depend on n.
Proof of Lemma 1. We see that
 \begin{equation} \bar \rho_{n,\alpha} (t) = \frac{e^{\alpha (d-1)(R_n-t)} \bigl( 1-e^{-2\alpha (R_n-t)} \bigr)^{d-1} }{\int_0^{R_n} e^{\alpha (d-1)s} \bigl( 1-e^{-2\alpha s} \bigr)^{d-1} ds}.\end{equation}
\begin{equation} \bar \rho_{n,\alpha} (t) = \frac{e^{\alpha (d-1)(R_n-t)} \bigl( 1-e^{-2\alpha (R_n-t)} \bigr)^{d-1} }{\int_0^{R_n} e^{\alpha (d-1)s} \bigl( 1-e^{-2\alpha s} \bigr)^{d-1} ds}.\end{equation}
Applying the binomial expansion
 \begin{align*}\bigl( 1-e^{-2\alpha s} \bigr)^{d-1} = \sum_{k=0}^{d-1} \begin{pmatrix} d-1 \\ k \end{pmatrix} (\!-1)^k e^{-2\alpha ks}, \, \, s > 0,\end{align*}
\begin{align*}\bigl( 1-e^{-2\alpha s} \bigr)^{d-1} = \sum_{k=0}^{d-1} \begin{pmatrix} d-1 \\ k \end{pmatrix} (\!-1)^k e^{-2\alpha ks}, \, \, s > 0,\end{align*}
we find that
![]() $\int_0^{R_n} e^{\alpha (d-1)s}ds$
is asymptotically the leading term in the denominator in (26). Using the obvious inequality
$\int_0^{R_n} e^{\alpha (d-1)s}ds$
is asymptotically the leading term in the denominator in (26). Using the obvious inequality
![]() $ \bigl( 1-e^{-2\alpha (R_n-t)} \bigr)^{d-1} \leq 1$
, we complete the proof of (i).
$ \bigl( 1-e^{-2\alpha (R_n-t)} \bigr)^{d-1} \leq 1$
, we complete the proof of (i).
For the proof of (ii), we need to handle the numerator of (26) as well. By another application of the binomial expansion, we have that
 \begin{align*}e^{\alpha (d-1) (R_n-t)}\, \Bigg[ \, 1+ \sum_{k=1}^{d-1} \begin{pmatrix} d-1 \\ k \end{pmatrix} (\!-\!1)^k e^{-2\alpha k(R_n-t)} \, \Bigg] = e^{\alpha (d-1) (R_n-t)} \bigl(1+o(1) \bigr)\end{align*}
\begin{align*}e^{\alpha (d-1) (R_n-t)}\, \Bigg[ \, 1+ \sum_{k=1}^{d-1} \begin{pmatrix} d-1 \\ k \end{pmatrix} (\!-\!1)^k e^{-2\alpha k(R_n-t)} \, \Bigg] = e^{\alpha (d-1) (R_n-t)} \bigl(1+o(1) \bigr)\end{align*}
uniformly for
![]() $0 \leq t \leq \lambda R_n$
, where
$0 \leq t \leq \lambda R_n$
, where
![]() $0 < \lambda <1$
.
$0 < \lambda <1$
.
3.1. Lemmas on hyperbolic distance
We first present a crucial lemma that explains why we consider (not necessarily induced) sub-trees, which are counted as injective homomorphisms in the hyperbolic random geometric graph. In particular, the conditional independence proven in Lemma 2 below does not hold for more general subgraph counts. The asymptotics of general subgraph counts is highly non-trivial not only for ‘induced’ sub-tree counts, but also for even seemingly simple triangle counts. For the latter case, [Reference Candellero and Fountoulakis14] introduced the notion of a global clustering coefficient defined as three times the ratio of the number of triangles to the number of paths of length two.
Lemma 2. Let
![]() $\Gamma_k$
be a tree on k vertices with edge set E. Let
$\Gamma_k$
be a tree on k vertices with edge set E. Let
![]() $X_1,\dots, X_k$
be i.i.d. random points with common density
$X_1,\dots, X_k$
be i.i.d. random points with common density
![]() $\rho_{n,\alpha} \otimes \pi$
. Define
$\rho_{n,\alpha} \otimes \pi$
. Define
![]() $T_i=R_n-d_\zeta(0,X_i)$
,
$T_i=R_n-d_\zeta(0,X_i)$
,
![]() $i=1,\dots,k$
, and write
$i=1,\dots,k$
, and write
![]() ${\textbf{T}} = (T_1,\dots,T_k)$
. Then it holds that
${\textbf{T}} = (T_1,\dots,T_k)$
. Then it holds that
Proof. Let
![]() $\Theta_i$
be the angular part of
$\Theta_i$
be the angular part of
![]() $X_i$
,
$X_i$
,
![]() $i=1,\dots,k$
. For the proof, it suffices to show that
$i=1,\dots,k$
. For the proof, it suffices to show that
Let us denote by
![]() $\Theta_{12}$
the relative angle between
$\Theta_{12}$
the relative angle between
![]() $\Theta_1$
and
$\Theta_1$
and
![]() $\Theta_2$
. Then, because of the uniformity of the angular density of
$\Theta_2$
. Then, because of the uniformity of the angular density of
![]() $\Theta_i$
in (5), we can derive that the density
$\Theta_i$
in (5), we can derive that the density
![]() $\pi_{rel}$
of
$\pi_{rel}$
of
![]() $\Theta_{12}$
, which is also the same as the conditional density of
$\Theta_{12}$
, which is also the same as the conditional density of
![]() $\Theta_{12} | \Theta_1$
, is given by
$\Theta_{12} | \Theta_1$
, is given by
Note that
![]() $d_\zeta(X_1,X_2)$
depends only on
$d_\zeta(X_1,X_2)$
depends only on
![]() $T_1,T_2,\Theta_{12}$
, and so we obtain that
$T_1,T_2,\Theta_{12}$
, and so we obtain that
Suppose that
![]() $\Gamma_k$
is of depth 1 rooted at vertex 1. In this case, since
$\Gamma_k$
is of depth 1 rooted at vertex 1. In this case, since
![]() $X_2,\dots,X_k$
are i.i.d.,
$X_2,\dots,X_k$
are i.i.d.,
 \begin{align*}\mathbb{P} \bigl( \, d_\zeta(X_1,X_j) \leq R_n, \ j=2,\dots,k\, |\, \Theta_1, {\textbf{T}} \bigr) &= \prod_{j=2}^k \mathbb{P}\bigl( \, d_\zeta(X_1,X_j)\leq R_n \, | \Theta_1, {\textbf{T}}) \\[3pt]&= \prod_{j=2}^k \mathbb{P}\bigl( \, d_\zeta(X_1,X_j)\leq R_n \, | {\textbf{T}}) \ \ a.s.\end{align*}
\begin{align*}\mathbb{P} \bigl( \, d_\zeta(X_1,X_j) \leq R_n, \ j=2,\dots,k\, |\, \Theta_1, {\textbf{T}} \bigr) &= \prod_{j=2}^k \mathbb{P}\bigl( \, d_\zeta(X_1,X_j)\leq R_n \, | \Theta_1, {\textbf{T}}) \\[3pt]&= \prod_{j=2}^k \mathbb{P}\bigl( \, d_\zeta(X_1,X_j)\leq R_n \, | {\textbf{T}}) \ \ a.s.\end{align*}
Suppose, for induction, that (27) holds for any tree
![]() $\Gamma_k$
rooted at vertex 1 with depth
$\Gamma_k$
rooted at vertex 1 with depth
![]() $M \geq 1$
. Assume subsequently that
$M \geq 1$
. Assume subsequently that
![]() $\Gamma_k$
is rooted at vertex 1 with depth
$\Gamma_k$
is rooted at vertex 1 with depth
![]() $M+1$
. Let
$M+1$
. Let
![]() $2,\dots,m$
be the vertices connected to 1, and
$2,\dots,m$
be the vertices connected to 1, and
![]() $S_2,\dots,S_m$
the corresponding trees rooted at
$S_2,\dots,S_m$
the corresponding trees rooted at
![]() $2,\dots,m$
. Let
$2,\dots,m$
. Let
![]() $E(S_\ell)$
be the edge set of
$E(S_\ell)$
be the edge set of
![]() $S_\ell$
. Then, from the disjointness of the trees and independence of the points
$S_\ell$
. Then, from the disjointness of the trees and independence of the points
![]() $X_i$
, we have
$X_i$
, we have
Now, an application of conditional expectations for each
![]() $\ell=2,\dots,m$
gives us the desired result as follows:
$\ell=2,\dots,m$
gives us the desired result as follows:
 \begin{align*}&\mathbb{P}\bigl( \, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E(S_\ell)\, | \, \Theta_1, {\textbf{T}} \bigr) \\[3pt]&= \mathbb{E} \Bigl[ \, {\textbf{1}}\bigl\{ d_\zeta(X_1,X_\ell) \leq R_n \bigr\}\, \mathbb{P} \bigl( \, d_\zeta(X_i,X_j)\leq R_n, \ (i,j)\in E(S_\ell)\setminus \{(1,\ell) \}\, | \, \Theta_\ell, {\textbf{T}} \bigr) \bigl| \, \Theta_1, {\textbf{T}} \Bigr] \\[3pt]&= \mathbb{E} \Bigg[ \, {\textbf{1}}\bigl\{ d_\zeta(X_1,X_\ell) \leq R_n \bigr\} \prod_{(i,j)\in E(S_\ell)\setminus \{ (1,\ell) \}} \mathbb{P} \bigl( \, d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{T}} \bigr) \bigl| \, \Theta_1,{\textbf{T}} \Bigg] \\[3pt] &=\prod_{(i,j)\in E(S_\ell)} \mathbb{P} \bigl( \, d_\zeta(X_i,X_j)\leq R_n\, | \, {\textbf{T}} \bigr) \ \ a.s.,\end{align*}
\begin{align*}&\mathbb{P}\bigl( \, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E(S_\ell)\, | \, \Theta_1, {\textbf{T}} \bigr) \\[3pt]&= \mathbb{E} \Bigl[ \, {\textbf{1}}\bigl\{ d_\zeta(X_1,X_\ell) \leq R_n \bigr\}\, \mathbb{P} \bigl( \, d_\zeta(X_i,X_j)\leq R_n, \ (i,j)\in E(S_\ell)\setminus \{(1,\ell) \}\, | \, \Theta_\ell, {\textbf{T}} \bigr) \bigl| \, \Theta_1, {\textbf{T}} \Bigr] \\[3pt]&= \mathbb{E} \Bigg[ \, {\textbf{1}}\bigl\{ d_\zeta(X_1,X_\ell) \leq R_n \bigr\} \prod_{(i,j)\in E(S_\ell)\setminus \{ (1,\ell) \}} \mathbb{P} \bigl( \, d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{T}} \bigr) \bigl| \, \Theta_1,{\textbf{T}} \Bigg] \\[3pt] &=\prod_{(i,j)\in E(S_\ell)} \mathbb{P} \bigl( \, d_\zeta(X_i,X_j)\leq R_n\, | \, {\textbf{T}} \bigr) \ \ a.s.,\end{align*}
where the induction hypothesis is used for the second equality, and (29) for the third equality.
We now mention some lemmas that help us to approximate the Poincaré metric. Given
![]() $u_1,u_2 \in B(0,R_n)$
, let
$u_1,u_2 \in B(0,R_n)$
, let
![]() $\theta_{12} \in [0,\pi]$
be the relative angle between the two vectors
$\theta_{12} \in [0,\pi]$
be the relative angle between the two vectors
![]() $\overrightarrow {Ou_1}$
and
$\overrightarrow {Ou_1}$
and
![]() $\overrightarrow {Ou_2}$
, where O denotes the origin of
$\overrightarrow {Ou_2}$
, where O denotes the origin of
![]() $B_d^{(\zeta)}$
. We also define
$B_d^{(\zeta)}$
. We also define
![]() $t_i = R_n-d_\zeta(0,u_i)$
,
$t_i = R_n-d_\zeta(0,u_i)$
,
![]() $i=1,2$
.
$i=1,2$
.
Lemma 3. Set
![]() $\hat \theta_{12} = \bigl(e^{-2 \zeta(R_n-t_1)}+ e^{-2 \zeta(R_n-t_2)} \bigr)^{1/2}$
. If
$\hat \theta_{12} = \bigl(e^{-2 \zeta(R_n-t_1)}+ e^{-2 \zeta(R_n-t_2)} \bigr)^{1/2}$
. If
![]() $\hat \theta_{12} / \theta_{12}$
vanishes as
$\hat \theta_{12} / \theta_{12}$
vanishes as
![]() $n\to\infty$
, then
$n\to\infty$
, then
 \begin{align*}d_\zeta(u_1,u_2) = 2R_n -(t_1+t_2) + \frac{2}{\zeta}\log \sin \left( \frac{\theta_{12}}{2} \right) + O \left( \left( \frac{\hat \theta_{12}}{\theta_{12}} \right)^2 \right), \ \ \ n\to\infty,\end{align*}
\begin{align*}d_\zeta(u_1,u_2) = 2R_n -(t_1+t_2) + \frac{2}{\zeta}\log \sin \left( \frac{\theta_{12}}{2} \right) + O \left( \left( \frac{\hat \theta_{12}}{\theta_{12}} \right)^2 \right), \ \ \ n\to\infty,\end{align*}
uniformly for all
![]() $u_1,u_2$
, with
$u_1,u_2$
, with
![]() $t_1+ t_2 \leq R_n-\omega_n$
, where
$t_1+ t_2 \leq R_n-\omega_n$
, where
![]() $\omega_n=\log \log R_n$
.
$\omega_n=\log \log R_n$
.
Proof. Fix a great circle of
![]() $B(0,R_n)$
spanned by
$B(0,R_n)$
spanned by
![]() $\overrightarrow{Ou_1}$
and
$\overrightarrow{Ou_1}$
and
![]() $\overrightarrow{Ou_2}$
. Then the hyperbolic law of cosines yields
$\overrightarrow{Ou_2}$
. Then the hyperbolic law of cosines yields
Since this great circle is a two-dimensional subspace of
![]() $B(0,R_n)$
, the rest of the argument is exactly the same as that for Lemma 2.3 in [Reference Fountoulakis19].
$B(0,R_n)$
, the rest of the argument is exactly the same as that for Lemma 2.3 in [Reference Fountoulakis19].
Lemma 4. In terms of the hyperbolic polar coordinates, let
![]() $X_1 = (t_1,\Theta_1)$
,
$X_1 = (t_1,\Theta_1)$
,
![]() $X_2 = (t_2,\Theta_2)$
, where
$X_2 = (t_2,\Theta_2)$
, where
![]() $\Theta_1,\Theta_2$
are i.i.d. random vectors on
$\Theta_1,\Theta_2$
are i.i.d. random vectors on
![]() $C_d$
with density
$C_d$
with density
![]() $\pi$
, and
$\pi$
, and
![]() $t_1,t_2$
are deterministic, representing the hyperbolic distance from the boundary. With the setup in Lemma 3,
$t_1,t_2$
are deterministic, representing the hyperbolic distance from the boundary. With the setup in Lemma 3,
uniformly on
![]() $\bigl\{(t_1,t_2)\,{:}\, t_1+t_2 \leq R_n-\omega_n \bigr\}$
, where
$\bigl\{(t_1,t_2)\,{:}\, t_1+t_2 \leq R_n-\omega_n \bigr\}$
, where
![]() $\kappa_{d-2} = \int_0^\pi \sin^{d-2} \theta\, d\theta$
and
$\kappa_{d-2} = \int_0^\pi \sin^{d-2} \theta\, d\theta$
and
![]() $\omega_n=\log \log R_n$
.
$\omega_n=\log \log R_n$
.
Proof. We again denote the relative angle between
![]() $\Theta_1$
and
$\Theta_1$
and
![]() $\Theta_2$
by
$\Theta_2$
by
![]() $\Theta_{12}$
. Recall that
$\Theta_{12}$
. Recall that
![]() $\Theta_{12} \stackrel{d}{=} \Theta_{12} | \Theta_1$
. From the hyperbolic law of cosines, we know that the distance between
$\Theta_{12} \stackrel{d}{=} \Theta_{12} | \Theta_1$
. From the hyperbolic law of cosines, we know that the distance between
![]() $X_1$
and
$X_1$
and
![]() $X_2$
is determined by
$X_2$
is determined by
![]() $t_1,t_2$
and their relative angle
$t_1,t_2$
and their relative angle
![]() $\Theta_{12}$
. Since
$\Theta_{12}$
. Since
![]() $t_1,t_2$
are fixed, by (28) we can write
$t_1,t_2$
are fixed, by (28) we can write
 \begin{align*}\mathbb{P}\bigl( \, d_\zeta(X_1,X_2)\leq R_n \bigr) &= \int_{C_d^2} {\textbf{1}} \bigl\{ \, d_\zeta(u_1,u_2) \leq R_n \bigr\}\, \pi(\theta_1)\pi(\theta_2)\, d\theta_1 d\theta_2 \\[3pt] &= \frac{1}{\kappa_{d-2}}\, \int_0^\pi {\textbf{1}} \bigl\{ \, d_\zeta(u_1,u_2) \leq R_n \bigr\}\, \sin^{d-2} \theta_{12} d\theta_{12},\end{align*}
\begin{align*}\mathbb{P}\bigl( \, d_\zeta(X_1,X_2)\leq R_n \bigr) &= \int_{C_d^2} {\textbf{1}} \bigl\{ \, d_\zeta(u_1,u_2) \leq R_n \bigr\}\, \pi(\theta_1)\pi(\theta_2)\, d\theta_1 d\theta_2 \\[3pt] &= \frac{1}{\kappa_{d-2}}\, \int_0^\pi {\textbf{1}} \bigl\{ \, d_\zeta(u_1,u_2) \leq R_n \bigr\}\, \sin^{d-2} \theta_{12} d\theta_{12},\end{align*}
where we write
![]() $u_i=(t_i,\theta_i)$
,
$u_i=(t_i,\theta_i)$
,
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $\theta_{12}$
is the relative angle between
$\theta_{12}$
is the relative angle between
![]() $u_1$
and
$u_1$
and
![]() $u_2$
. Now, we shall approximate the above integral. Let
$u_2$
. Now, we shall approximate the above integral. Let
![]() $A_{12} = e^{\zeta (R_n-t_1-t_2)/2}$
. Claim 2.5 in [Reference Fountoulakis19] proves that
$A_{12} = e^{\zeta (R_n-t_1-t_2)/2}$
. Claim 2.5 in [Reference Fountoulakis19] proves that
![]() $A_{12}^{-1} / (\omega_n \hat \theta_{12}) \to \infty$
as
$A_{12}^{-1} / (\omega_n \hat \theta_{12}) \to \infty$
as
![]() $n\to\infty$
. By virtue of Lemma 3, along with
$n\to\infty$
. By virtue of Lemma 3, along with
![]() $A_{12}^{-1} \to 0$
as
$A_{12}^{-1} \to 0$
as
![]() $n\to\infty$
, we have, on the set
$n\to\infty$
, we have, on the set
![]() $\{ (t_1,t_2): t_1+t_2 \leq R_n-\omega_n \}$
,
$\{ (t_1,t_2): t_1+t_2 \leq R_n-\omega_n \}$
,
 \begin{align*}\int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \bigl\{\, d_\zeta(u_1,u_2) \leq R_n \, \bigr\}\, \sin^{d-2} \theta_{12}\, d\theta_{12} &\sim \int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \Big\{\, \sin \Big(\frac{\theta_{12}}{2}\Big) \leq A_{12}^{-1} \, \Big\}\,\sin^{d-2} \theta_{12}\, d\theta_{12} \\[3pt]\sim \int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \left\{ \theta_{12} \leq 2 A_{12}^{-1} \right\}\, (\theta_{12})^{d-2}\, d\theta_{12} \, & \sim \, \frac{(2A_{12}^{-1})^{d-1}}{d-1}.\end{align*}
\begin{align*}\int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \bigl\{\, d_\zeta(u_1,u_2) \leq R_n \, \bigr\}\, \sin^{d-2} \theta_{12}\, d\theta_{12} &\sim \int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \Big\{\, \sin \Big(\frac{\theta_{12}}{2}\Big) \leq A_{12}^{-1} \, \Big\}\,\sin^{d-2} \theta_{12}\, d\theta_{12} \\[3pt]\sim \int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \left\{ \theta_{12} \leq 2 A_{12}^{-1} \right\}\, (\theta_{12})^{d-2}\, d\theta_{12} \, & \sim \, \frac{(2A_{12}^{-1})^{d-1}}{d-1}.\end{align*}
Therefore,
 \begin{align*}&\int_{0}^\pi {\textbf{1}} \bigl\{\, d_\zeta(u_1,u_2) \leq R_n \, \bigr\}\, \sin^{d-2}\theta_{12}\, d\theta_{12} \\& \quad = o\big(A_{12}^{-(d-1)}\big) + \int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \bigl\{\, d_\zeta(u_1,u_2) \leq R_n \, \bigr\}\, \sin^{d-2}\theta_{12}\, d\theta_{12} \sim \frac{\left(2A_{12}^{-1}\right)s^{d-1}}{d-1}, \ \ \ n\to\infty,\end{align*}
\begin{align*}&\int_{0}^\pi {\textbf{1}} \bigl\{\, d_\zeta(u_1,u_2) \leq R_n \, \bigr\}\, \sin^{d-2}\theta_{12}\, d\theta_{12} \\& \quad = o\big(A_{12}^{-(d-1)}\big) + \int_{A_{12}^{-1}/\omega_n}^\pi {\textbf{1}} \bigl\{\, d_\zeta(u_1,u_2) \leq R_n \, \bigr\}\, \sin^{d-2}\theta_{12}\, d\theta_{12} \sim \frac{\left(2A_{12}^{-1}\right)s^{d-1}}{d-1}, \ \ \ n\to\infty,\end{align*}
as required.
3.2. Proofs of the expectation and variance results
In what follows, we calculate the moments of
![]() $S_n^{(\gamma)}$
. We first introduce some notation to save space. For
$S_n^{(\gamma)}$
. We first introduce some notation to save space. For
![]() $u_i \in B(0,R_n)$
,
$u_i \in B(0,R_n)$
,
![]() $i=1,\dots,k$
, we write
$i=1,\dots,k$
, we write
and
where
![]() $t_i=R_n-d_\zeta(0,u_i)$
. Note that
$t_i=R_n-d_\zeta(0,u_i)$
. Note that
![]() $g_{n,\gamma}$
represents the product of multiple indicator functions in the right-hand side of (10), while
$g_{n,\gamma}$
represents the product of multiple indicator functions in the right-hand side of (10), while
![]() $h_{n,\gamma}$
is a similar indicator for
$h_{n,\gamma}$
is a similar indicator for
![]() $S_n - S_n^{(\gamma)}$
.
$S_n - S_n^{(\gamma)}$
.
Proof of Theorem 1. Let
![]() $X_1,\ldots,X_k$
be i.i.d. random points with density
$X_1,\ldots,X_k$
be i.i.d. random points with density
![]() $\rho_{n,\alpha} \otimes \pi$
, and set
$\rho_{n,\alpha} \otimes \pi$
, and set
![]() $T_i = R_n - d_\zeta(0,X_i)$
as before. By an application of the multivariate Mecke formula for Poisson processes (see, e.g., [Reference Last and Penrose33, Chapter 4]),
$T_i = R_n - d_\zeta(0,X_i)$
as before. By an application of the multivariate Mecke formula for Poisson processes (see, e.g., [Reference Last and Penrose33, Chapter 4]),
 \begin{align}\mathbb{E} \big( S_n^{(\gamma)} \big) &= n^k \, \mathbb{E}\bigl( g_{n,\gamma}(X_1,\ldots,X_k)\bigr)\nonumber\\[3pt] &= n^k\, \mathbb{E} \bigl[ g_{n,\gamma}(X_1,\ldots,X_k) \prod_{(i,j) \in E} {\textbf{1}} \{ T_i + T_j \leq R_n - \omega_n \} \bigr] \notag \\[3pt]&\qquad + n^k\, \mathbb{E} \bigl[ g_{n,\gamma}(X_1,\ldots,X_k) {\textbf{1}}\bigl\{ \cup_{(i,j) \in E} \{T_i+T_j > R_n-\omega_n\} \bigr\} \bigr] \notag \\[3pt]& \,{=\!:}\, A_n + B_n, \end{align}
\begin{align}\mathbb{E} \big( S_n^{(\gamma)} \big) &= n^k \, \mathbb{E}\bigl( g_{n,\gamma}(X_1,\ldots,X_k)\bigr)\nonumber\\[3pt] &= n^k\, \mathbb{E} \bigl[ g_{n,\gamma}(X_1,\ldots,X_k) \prod_{(i,j) \in E} {\textbf{1}} \{ T_i + T_j \leq R_n - \omega_n \} \bigr] \notag \\[3pt]&\qquad + n^k\, \mathbb{E} \bigl[ g_{n,\gamma}(X_1,\ldots,X_k) {\textbf{1}}\bigl\{ \cup_{(i,j) \in E} \{T_i+T_j > R_n-\omega_n\} \bigr\} \bigr] \notag \\[3pt]& \,{=\!:}\, A_n + B_n, \end{align}
where
![]() $\omega_n=\log \log R_n$
. From now on, the argument aims to show that
$\omega_n=\log \log R_n$
. From now on, the argument aims to show that
![]() $A_n$
coincides asymptotically with the right-hand side of (11). It follows from the conditioning on the radial distances of
$A_n$
coincides asymptotically with the right-hand side of (11). It follows from the conditioning on the radial distances of
![]() $X_1,\dots,X_k$
from the boundary and Lemma 2 that
$X_1,\dots,X_k$
from the boundary and Lemma 2 that
 \begin{align*}A_n &= n^k \mathbb{E} \Bigg[\ {\textbf{1}} \bigl\{ T_i +T_j \leq R_n-\omega_n, \ (i,j)\in E, \ T_i \leq \gamma R_n, \ i=1,\dots,k \bigr\} \prod_{(i,j)\in E} \\&\quad \times \mathbb{P}\bigl( \, d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{T}}\bigr) \Bigg],\end{align*}
\begin{align*}A_n &= n^k \mathbb{E} \Bigg[\ {\textbf{1}} \bigl\{ T_i +T_j \leq R_n-\omega_n, \ (i,j)\in E, \ T_i \leq \gamma R_n, \ i=1,\dots,k \bigr\} \prod_{(i,j)\in E} \\&\quad \times \mathbb{P}\bigl( \, d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{T}}\bigr) \Bigg],\end{align*}
where
![]() ${\textbf{T}}=(T_1,\dots,T_k)$
. Setting
${\textbf{T}}=(T_1,\dots,T_k)$
. Setting
![]() ${\textbf{t}} = (t_1,\dots,t_k)$
, we may write
${\textbf{t}} = (t_1,\dots,t_k)$
, we may write
 \begin{align}A_n &= n^k\, \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_k\, {\textbf{1}} \bigl\{ t_i + t_j \leq R_n-\omega_n, \ (i,j)\in E\, \bigr\} \nonumber\\[3pt]&\qquad \qquad \qquad \qquad \qquad \qquad \times \prod_{(i,j)\in E} \mathbb{P}\bigl( d_\zeta(X_i,X_j) \leq R_n\, |\, {\textbf{t}} \bigr) \, \bar \rho_{n,\alpha} ({\textbf{t}}), \end{align}
\begin{align}A_n &= n^k\, \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_k\, {\textbf{1}} \bigl\{ t_i + t_j \leq R_n-\omega_n, \ (i,j)\in E\, \bigr\} \nonumber\\[3pt]&\qquad \qquad \qquad \qquad \qquad \qquad \times \prod_{(i,j)\in E} \mathbb{P}\bigl( d_\zeta(X_i,X_j) \leq R_n\, |\, {\textbf{t}} \bigr) \, \bar \rho_{n,\alpha} ({\textbf{t}}), \end{align}
where
![]() $\bar \rho_{n,\alpha} ({\textbf{t}})$
denotes the product of densities in (7):
$\bar \rho_{n,\alpha} ({\textbf{t}})$
denotes the product of densities in (7):
 \begin{align*}\bar \rho_{n,\alpha} ({\textbf{t}}) \,{:\!=}\, \prod_{i=1}^k \bar \rho_{n,\alpha} (t_i). \end{align*}
\begin{align*}\bar \rho_{n,\alpha} ({\textbf{t}}) \,{:\!=}\, \prod_{i=1}^k \bar \rho_{n,\alpha} (t_i). \end{align*}
Applying Lemma 4 on the set
![]() $\bigl\{ t_i+t_j \leq R_n -\omega_n, \ (i,j)\in E \bigr\}$
, we have, as
$\bigl\{ t_i+t_j \leq R_n -\omega_n, \ (i,j)\in E \bigr\}$
, we have, as
![]() $n\to\infty$
,
$n\to\infty$
,
 \begin{align*}\prod_{(i,j)\in E} \mathbb{P}(d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}}) &\sim \prod_{(i,j)\in E} \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\, e^{-\zeta (d-1) (R_n-t_i-t_j)/2} \\[3pt]&= \Bigg( \frac{2^{d-1}}{(d-1)\kappa_{d-2}} \Bigg)^{k-1} e^{-[(k-1)R_n - \sum_{i=1}^k d_it_i]\zeta (d-1)/2}.\end{align*}
\begin{align*}\prod_{(i,j)\in E} \mathbb{P}(d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}}) &\sim \prod_{(i,j)\in E} \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\, e^{-\zeta (d-1) (R_n-t_i-t_j)/2} \\[3pt]&= \Bigg( \frac{2^{d-1}}{(d-1)\kappa_{d-2}} \Bigg)^{k-1} e^{-[(k-1)R_n - \sum_{i=1}^k d_it_i]\zeta (d-1)/2}.\end{align*}
Furthermore, it follows from Lemma 1(ii) that
uniformly for
![]() $t_i \leq \gamma R_n$
,
$t_i \leq \gamma R_n$
,
![]() $i=1,\dots,k$
. Substituting these results into (33), we obtain
$i=1,\dots,k$
. Substituting these results into (33), we obtain
 \begin{equation}A_n \sim \Bigg( \frac{2^{d-1}}{\kappa_{d-2}} \Bigg)^{k-1} \alpha^k (d-1) \, n^k e^{-\zeta(d-1)(k-1) R_n/2} \prod_{i=1}^k a_n^{(\gamma)}(d_i).\end{equation}
\begin{equation}A_n \sim \Bigg( \frac{2^{d-1}}{\kappa_{d-2}} \Bigg)^{k-1} \alpha^k (d-1) \, n^k e^{-\zeta(d-1)(k-1) R_n/2} \prod_{i=1}^k a_n^{(\gamma)}(d_i).\end{equation}
We now show that
![]() $B_n = o(A_n)$
as
$B_n = o(A_n)$
as
![]() $n\to\infty$
, unless
$n\to\infty$
, unless
![]() $\gamma =1/2$
. We check only the case in which there is an edge joining
$\gamma =1/2$
. We check only the case in which there is an edge joining
![]() $X_1$
and
$X_1$
and
![]() $X_2$
such that
$X_2$
such that
![]() $T_1+T_2 > R_n-\omega_n$
, while all the other edges satisfy
$T_1+T_2 > R_n-\omega_n$
, while all the other edges satisfy
![]() $T_i+T_j \leq R_n-\omega_n$
. However, the argument below can be applied in an obvious way even when multiple edges satisfy
$T_i+T_j \leq R_n-\omega_n$
. However, the argument below can be applied in an obvious way even when multiple edges satisfy
![]() $T_i + T_j >R_n-\omega_n$
. Specifically, we shall verify
$T_i + T_j >R_n-\omega_n$
. Specifically, we shall verify
 \begin{align}C_n &\,{:\!=}\, n^k\mathbb{P} \bigl( d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E, \ T_i \leq \gamma R_n, \ i=1,\dots,k, \nonumber\\[3pt] &\qquad \qquad \qquad T_1+T_2 > R_n-\omega_n, \ T_i + T_j \leq R_n-\omega_n, \ (i,j)\in E\setminus \{ (1,2)\} \bigr) = o(A_n). \end{align}
\begin{align}C_n &\,{:\!=}\, n^k\mathbb{P} \bigl( d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E, \ T_i \leq \gamma R_n, \ i=1,\dots,k, \nonumber\\[3pt] &\qquad \qquad \qquad T_1+T_2 > R_n-\omega_n, \ T_i + T_j \leq R_n-\omega_n, \ (i,j)\in E\setminus \{ (1,2)\} \bigr) = o(A_n). \end{align}
Proceeding in the same way as in the computation for
![]() $A_n$
, while applying the obvious bound
$A_n$
, while applying the obvious bound
we see that
 \begin{align*}C_n &\leq C^* n^k e^{-\zeta(d-1)(k-2)R_n/2} \prod_{i=3}^n a_n^{(\gamma)} (d_i) \\[3pt] &\quad \times \int_0^{\gamma R_n} \int_0^{\gamma R_n} e^{2^{-1}\zeta (d-1)\sum_{i=1}^2 (d_i - 1-2\alpha/ \zeta)t_i } {\textbf{1}} \bigl\{ t_1+t_2 >R_n-\omega_n \bigr\}dt_1 dt_2.\end{align*}
\begin{align*}C_n &\leq C^* n^k e^{-\zeta(d-1)(k-2)R_n/2} \prod_{i=3}^n a_n^{(\gamma)} (d_i) \\[3pt] &\quad \times \int_0^{\gamma R_n} \int_0^{\gamma R_n} e^{2^{-1}\zeta (d-1)\sum_{i=1}^2 (d_i - 1-2\alpha/ \zeta)t_i } {\textbf{1}} \bigl\{ t_1+t_2 >R_n-\omega_n \bigr\}dt_1 dt_2.\end{align*}
By comparing this upper bound with the right-hand side of (11), we see that it suffices to show that
 \begin{align}D_n &\,{:\!=}\, e^{\zeta(d-1) R_n/2}\int_0^{\gamma R_n} \int_0^{\gamma R_n} e^{2^{-1} \zeta(d-1) \sum_{i=1}^2 (d_i - 1-2\alpha /\zeta)t_i } {\textbf{1}} \bigl\{ t_1+t_2 >R_n-\omega_n \bigr\}dt_1 dt_2 \nonumber\\[3pt]&= o \bigl( a_n^{(\gamma)} (d_1)a_n^{(\gamma)} (d_2) \bigr), \ \ n\to\infty. \end{align}
\begin{align}D_n &\,{:\!=}\, e^{\zeta(d-1) R_n/2}\int_0^{\gamma R_n} \int_0^{\gamma R_n} e^{2^{-1} \zeta(d-1) \sum_{i=1}^2 (d_i - 1-2\alpha /\zeta)t_i } {\textbf{1}} \bigl\{ t_1+t_2 >R_n-\omega_n \bigr\}dt_1 dt_2 \nonumber\\[3pt]&= o \bigl( a_n^{(\gamma)} (d_1)a_n^{(\gamma)} (d_2) \bigr), \ \ n\to\infty. \end{align}
If
![]() $0<\gamma<1/2$
, then
$0<\gamma<1/2$
, then
![]() $D_n$
is identically 0; hence, we may restrict ourselves to the case
$D_n$
is identically 0; hence, we may restrict ourselves to the case
![]() $1/2 < \gamma <1$
. Without loss of generality, we may assume that
$1/2 < \gamma <1$
. Without loss of generality, we may assume that
![]() $d_1 \geq d_2$
and rewrite
$d_1 \geq d_2$
and rewrite
![]() $D_n$
as
$D_n$
as
If
![]() $0 < 2 \alpha/\zeta< d_2-1$
, then
$0 < 2 \alpha/\zeta< d_2-1$
, then
 \begin{align*}D_n & \leq C^* e^{ \zeta (d-1) [R_n + \sum_{i=1}^2 (d_i-1 -2\alpha /\zeta)\gamma R_n]/2} \\[3pt] & = e^{ (1/2-\gamma)\zeta (d-1)R_n} O\bigl( a_n^{(\gamma)} (d_1)a_n^{(\gamma)} (d_2) \bigr) = o \bigl( a_n^{(\gamma)} (d_1)a_n^{(\gamma)} (d_2) \bigr).\end{align*}
\begin{align*}D_n & \leq C^* e^{ \zeta (d-1) [R_n + \sum_{i=1}^2 (d_i-1 -2\alpha /\zeta)\gamma R_n]/2} \\[3pt] & = e^{ (1/2-\gamma)\zeta (d-1)R_n} O\bigl( a_n^{(\gamma)} (d_1)a_n^{(\gamma)} (d_2) \bigr) = o \bigl( a_n^{(\gamma)} (d_1)a_n^{(\gamma)} (d_2) \bigr).\end{align*}
On the other hand, let
![]() $2 \alpha /\zeta> d_2-1$
. Then
$2 \alpha /\zeta> d_2-1$
. Then
The same result can also be obtained in the boundary case
![]() $2\alpha /\zeta= d_2-1$
, and thus we have proven (36). Finally, if
$2\alpha /\zeta= d_2-1$
, and thus we have proven (36). Finally, if
![]() $\gamma=1/2$
, the above calculations imply
$\gamma=1/2$
, the above calculations imply
and thus (12) follows.
We now proceed to proving (13). For
![]() $0<\gamma<1$
, define
$0<\gamma<1$
, define
![]() $U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
. Suppose
$U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
. Suppose
![]() $2 \alpha/\zeta > d_{(k)}$
. Appealing to (11), we obtain
$2 \alpha/\zeta > d_{(k)}$
. Appealing to (11), we obtain
 \begin{align*}\mathbb{E} \big( S_n^{(\gamma)} \big) \sim \biggl( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\biggr)^{k-1} \alpha^k \, \prod_{i=1}^k \bigl( \alpha - \zeta d_i/2 \bigr)^{-1} n^k e^{- \zeta(d-1) (k-1)R_n/2},\end{align*}
\begin{align*}\mathbb{E} \big( S_n^{(\gamma)} \big) \sim \biggl( \frac{2^{d-1}}{(d-1)\kappa_{d-2}}\biggr)^{k-1} \alpha^k \, \prod_{i=1}^k \bigl( \alpha - \zeta d_i/2 \bigr)^{-1} n^k e^{- \zeta(d-1) (k-1)R_n/2},\end{align*}
because, for every
![]() $i=1,\dots,k$
,
$i=1,\dots,k$
,
![]() $a_n^{(\gamma)} (d_i)$
converges to
$a_n^{(\gamma)} (d_i)$
converges to
![]() $(d-1)^{-1}\bigl( \alpha - \zeta d_i/2 \bigr)^{-1}$
. Therefore, to complete our proof, it suffices to verify that
$(d-1)^{-1}\bigl( \alpha - \zeta d_i/2 \bigr)^{-1}$
. Therefore, to complete our proof, it suffices to verify that
Recalling the notation (31), we apply the Mecke formula to obtain that
 \begin{align*}\mathbb{E} \left( U_n^{(\gamma)} \right) &= n^k\, \mathbb{E} \bigl( h_{n,\gamma} (X_1,\dots,X_k) \bigr) \\[3pt]&= n^k\, \mathbb{E} \bigl[ h_{n,\gamma} (X_1,\dots,X_k) \prod_{(i,j)\in E}{\textbf{1}} \{ T_i + T_j \leq R_n - \omega_n \} \bigr] \\[3pt]&\qquad + n^k\, \mathbb{E} \bigl[ h_{n,\gamma}(X_1,\ldots,X_k) {\textbf{1}} \bigl\{ \cup_{(i,j) \in E} \{T_i+T_j > R_n-\omega_n\} \bigr\} \bigr] \,{=\!:}\, A_n^{\prime} + B_n^{\prime}.\end{align*}
\begin{align*}\mathbb{E} \left( U_n^{(\gamma)} \right) &= n^k\, \mathbb{E} \bigl( h_{n,\gamma} (X_1,\dots,X_k) \bigr) \\[3pt]&= n^k\, \mathbb{E} \bigl[ h_{n,\gamma} (X_1,\dots,X_k) \prod_{(i,j)\in E}{\textbf{1}} \{ T_i + T_j \leq R_n - \omega_n \} \bigr] \\[3pt]&\qquad + n^k\, \mathbb{E} \bigl[ h_{n,\gamma}(X_1,\ldots,X_k) {\textbf{1}} \bigl\{ \cup_{(i,j) \in E} \{T_i+T_j > R_n-\omega_n\} \bigr\} \bigr] \,{=\!:}\, A_n^{\prime} + B_n^{\prime}.\end{align*}
We can calculate
![]() $A_n^\prime$
in almost the same manner as
$A_n^\prime$
in almost the same manner as
![]() $A_n$
; the only difference is that when handling
$A_n$
; the only difference is that when handling
![]() $\bar \rho_{n,\alpha} ({\textbf{t}})$
, we apply the inequality in Lemma 1(i) instead of Lemma 1(ii). We then obtain
$\bar \rho_{n,\alpha} ({\textbf{t}})$
, we apply the inequality in Lemma 1(i) instead of Lemma 1(ii). We then obtain
 \begin{align*}A_n^\prime &\leq C^* n^k e^{- \zeta(d-1)(k-1)R_n/2} \int_0^{R_n} dt_1 \cdots \int_0^{R_n} dt_k \\[3pt]& \qquad \qquad \times {\textbf{1}} \{ \, t_i > \gamma R_n \ \text{for some } i=1,\dots,k\, \}\, e^{2^{-1} \zeta (d-1)\sum_{i=1}^k (d_i - 2\alpha/ \zeta)t_i} \\[3pt]&= o\bigl( n^k e^{- \zeta(d-1)(k-1)R_n/2} \bigr).\end{align*}
\begin{align*}A_n^\prime &\leq C^* n^k e^{- \zeta(d-1)(k-1)R_n/2} \int_0^{R_n} dt_1 \cdots \int_0^{R_n} dt_k \\[3pt]& \qquad \qquad \times {\textbf{1}} \{ \, t_i > \gamma R_n \ \text{for some } i=1,\dots,k\, \}\, e^{2^{-1} \zeta (d-1)\sum_{i=1}^k (d_i - 2\alpha/ \zeta)t_i} \\[3pt]&= o\bigl( n^k e^{- \zeta(d-1)(k-1)R_n/2} \bigr).\end{align*}
Here, the second equality follows from the assumption that
![]() $d_i - 2\alpha /\zeta < 0$
for all
$d_i - 2\alpha /\zeta < 0$
for all
![]() $i=1,\dots,k$
. Furthermore, we can show that
$i=1,\dots,k$
. Furthermore, we can show that
![]() $B_n^{\prime} = o \bigl( n^k e^{-\zeta(d-1)(k-1)R_n/2} \bigr)$
; the proof of this is similar to that of the corresponding result for the derivation of (35) and (36), so we omit it. Thus, we have (37) as needed to complete the proof of the theorem.
$B_n^{\prime} = o \bigl( n^k e^{-\zeta(d-1)(k-1)R_n/2} \bigr)$
; the proof of this is similar to that of the corresponding result for the derivation of (35) and (36), so we omit it. Thus, we have (37) as needed to complete the proof of the theorem.
Proof of Corollary 1. Define
![]() $S_n^{(\gamma)}$
as the sub-tree counts relating to a k-star with
$S_n^{(\gamma)}$
as the sub-tree counts relating to a k-star with
![]() $d_{(k)} = k-1$
,
$d_{(k)} = k-1$
,
![]() $d_{(k-1)} = \cdots = d_{(1)} = 1$
:
$d_{(k-1)} = \cdots = d_{(1)} = 1$
:
We also define
![]() $U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
. First, (15) is a direct consequence of (13), so we shall prove only (ii) and (iii).
$U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
. First, (15) is a direct consequence of (13), so we shall prove only (ii) and (iii).
For the proof of (ii), we start by deriving a suitable upper bound for
![]() $\mathbb{E} \big( U_n^{(\gamma)}\big)$
. By the Mecke formula and Lemma 1(i),
$\mathbb{E} \big( U_n^{(\gamma)}\big)$
. By the Mecke formula and Lemma 1(i),
 \begin{align*}\mathbb{E}(U_n^{(\gamma)} ) &= n^k \, \mathbb{P} \bigl( d_\zeta(X_1,X_i) \leq R_n, \ i=2,\dots,k, \ T_i > \gamma R_n \ \text{for some } i=1,\dots,k\, \bigr)\\[3pt]&\leq n^k k \, \mathbb{P} ( T_1 > \gamma R_n\, ) \leq C^* n^k e^{-\alpha (d-1) \gamma R_n}R_n.\end{align*}
\begin{align*}\mathbb{E}(U_n^{(\gamma)} ) &= n^k \, \mathbb{P} \bigl( d_\zeta(X_1,X_i) \leq R_n, \ i=2,\dots,k, \ T_i > \gamma R_n \ \text{for some } i=1,\dots,k\, \bigr)\\[3pt]&\leq n^k k \, \mathbb{P} ( T_1 > \gamma R_n\, ) \leq C^* n^k e^{-\alpha (d-1) \gamma R_n}R_n.\end{align*}
Taking the logarithm on both sides, we get
On the other hand, it follows from Theorem 1 that
which implies that, as
![]() $n\to\infty$
,
$n\to\infty$
,
Moreover, if
![]() $\limsup_{n\to\infty} \mathbb{E}\left(U_n^{(\gamma)}\right) / \mathbb{E}\left(S_n^{(\gamma)}\right) < \infty$
,
$\limsup_{n\to\infty} \mathbb{E}\left(U_n^{(\gamma)}\right) / \mathbb{E}\left(S_n^{(\gamma)}\right) < \infty$
,
 \begin{align*}\limsup_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n \vee \log n} = \limsup_{n\to\infty} \frac{\log E\left(S_n^{(\gamma)}\right)}{R_n \vee \log n},\end{align*}
\begin{align*}\limsup_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n \vee \log n} = \limsup_{n\to\infty} \frac{\log E\left(S_n^{(\gamma)}\right)}{R_n \vee \log n},\end{align*}
and if
![]() $\limsup_{n\to\infty} \mathbb{E}\left(U_n^{(\gamma)}\right) / \mathbb{E}\left(S_n^{(\gamma)}\right) = \infty$
,
$\limsup_{n\to\infty} \mathbb{E}\left(U_n^{(\gamma)}\right) / \mathbb{E}\left(S_n^{(\gamma)}\right) = \infty$
,
 \begin{align*}\limsup_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n \vee \log n} = \limsup_{n\to\infty} \frac{\log E\left(U_n^{(\gamma)}\right)}{R_n \vee \log n}.\end{align*}
\begin{align*}\limsup_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n \vee \log n} = \limsup_{n\to\infty} \frac{\log E\left(U_n^{(\gamma)}\right)}{R_n \vee \log n}.\end{align*}
Therefore, using the obvious inequalities
 \begin{align*}\liminf_{n\to \infty} \frac{\log \mathbb{E} \left( S_n^{(\gamma)} \right)}{R_n\vee \log n} &\leq \liminf_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n \vee \log n} \leq \limsup_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n\vee \log n}\\[3pt]& \leq \limsup_{n\to\infty} \frac{\log \mathbb{E} \left( S_n^{(\gamma)} \right)}{R_n\vee \log n} \vee \limsup_{n\to\infty} \frac{\log \mathbb{E} \left(U_n^{(\gamma)} \right)}{R_n\vee \log n},\end{align*}
\begin{align*}\liminf_{n\to \infty} \frac{\log \mathbb{E} \left( S_n^{(\gamma)} \right)}{R_n\vee \log n} &\leq \liminf_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n \vee \log n} \leq \limsup_{n\to\infty} \frac{\log \mathbb{E} (S_n)}{R_n\vee \log n}\\[3pt]& \leq \limsup_{n\to\infty} \frac{\log \mathbb{E} \left( S_n^{(\gamma)} \right)}{R_n\vee \log n} \vee \limsup_{n\to\infty} \frac{\log \mathbb{E} \left(U_n^{(\gamma)} \right)}{R_n\vee \log n},\end{align*}
and letting
![]() $\gamma \nearrow 1$
, we obtain
$\gamma \nearrow 1$
, we obtain
The proof of (iii) is very similar to that of (ii), so we omit it.
Proof of Theorem 2. We start by writing
 \begin{align*}\mathbb{E} \bigl[ (S_n^{(\gamma)})^2 \bigr]&= \sum_{\ell =0}^k \mathbb{E} \Bigg[ \sum_{(X_1,\dots,X_{2k-\ell}) \in \mathcal P_{n,\neq}^{2k-\ell}} g_{n,\gamma} (X_1,\dots,X_k)\,\\&\qquad \qquad \qquad\qquad \times g_{n,\gamma}(X_1,\dots,X_\ell,X_{k+1},\dots,X_{2k-\ell}) \Bigg] \,{=\!:}\, \sum_{\ell = 0}^k \mathbb{E} ( I_\ell ),\end{align*}
\begin{align*}\mathbb{E} \bigl[ (S_n^{(\gamma)})^2 \bigr]&= \sum_{\ell =0}^k \mathbb{E} \Bigg[ \sum_{(X_1,\dots,X_{2k-\ell}) \in \mathcal P_{n,\neq}^{2k-\ell}} g_{n,\gamma} (X_1,\dots,X_k)\,\\&\qquad \qquad \qquad\qquad \times g_{n,\gamma}(X_1,\dots,X_\ell,X_{k+1},\dots,X_{2k-\ell}) \Bigg] \,{=\!:}\, \sum_{\ell = 0}^k \mathbb{E} ( I_\ell ),\end{align*}
where
![]() $g_{n,\gamma}$
is defined at (30). For
$g_{n,\gamma}$
is defined at (30). For
![]() $\ell = 0$
, the Mecke formula yields
$\ell = 0$
, the Mecke formula yields
Let
![]() $\Gamma^{(i,j)}_{2k-1}$
be a tree on
$\Gamma^{(i,j)}_{2k-1}$
be a tree on
![]() $[2k-1]$
(meaning
$[2k-1]$
(meaning
![]() $|E| = 2k-2$
) formed by taking two copies of
$|E| = 2k-2$
) formed by taking two copies of
![]() $\Gamma_k$
and identifying the vertex of degree
$\Gamma_k$
and identifying the vertex of degree
![]() $d_i$
in one copy with the vertex of degree
$d_i$
in one copy with the vertex of degree
![]() $d_j$
in the other copy. In other words, the degree sequence of
$d_j$
in the other copy. In other words, the degree sequence of
![]() $\Gamma^{(i,j)}_{2k-1}$
is
$\Gamma^{(i,j)}_{2k-1}$
is
![]() $d_i + d_j, d_i, d_j$
and a pair of
$d_i + d_j, d_i, d_j$
and a pair of
![]() $d_\ell$
’s for
$d_\ell$
’s for
![]() $\ell \in [k] \setminus \{i,j\}$
; see Figure 4(a)–(b).
$\ell \in [k] \setminus \{i,j\}$
; see Figure 4(a)–(b).

Figure 4. (a) Let
![]() $k=5$
,
$k=5$
,
![]() $i=1$
, and
$i=1$
, and
![]() $j=3$
. Take two copies of
$j=3$
. Take two copies of
![]() $\Gamma_5$
. (b) Identify vertex 1 in one copy and vertex 3 in the other copy, and glue them together. The vertex ‘a’ denotes the glued vertex. The degree sequence of
$\Gamma_5$
. (b) Identify vertex 1 in one copy and vertex 3 in the other copy, and glue them together. The vertex ‘a’ denotes the glued vertex. The degree sequence of
![]() $\Gamma_9^{(1,3)}$
is
$\Gamma_9^{(1,3)}$
is
![]() $\{5, 2, 3, 1, 1, 1, 1, 1, 1\}$
. (c) Consider the same
$\{5, 2, 3, 1, 1, 1, 1, 1, 1\}$
. (c) Consider the same
![]() $\Gamma_5$
as in (a) and set
$\Gamma_5$
as in (a) and set
![]() $\ell=2$
. Glue vertex 2 in one copy of
$\ell=2$
. Glue vertex 2 in one copy of
![]() $\Gamma_5$
to vertex 2 in the other copy. Do the same for vertex 3 for the two copies of
$\Gamma_5$
to vertex 2 in the other copy. Do the same for vertex 3 for the two copies of
![]() $\Gamma_5$
; this yields the subgraph H shown here. (d) Removing an edge (a, b) from H, we get one of the corresponding spanning trees.
$\Gamma_5$
; this yields the subgraph H shown here. (d) Removing an edge (a, b) from H, we get one of the corresponding spanning trees.
We first note that
![]() $I_1 = \sum_{i,j=1}^k {\mathcal{C}}\Big(\Gamma^{(i,j)}_{2k-1},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\Big)$
, and so, from the identity for
$I_1 = \sum_{i,j=1}^k {\mathcal{C}}\Big(\Gamma^{(i,j)}_{2k-1},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\Big)$
, and so, from the identity for
![]() $\mathbb{E}(I_0)$
above, we have that
$\mathbb{E}(I_0)$
above, we have that
 \begin{align}\mathbb{V}ar(S_n^{(\gamma)}) &= \sum_{\ell =1}^k \mathbb{E}( I_\ell ) \geq \mathbb{E} ( I_1 ) \geq E\Bigl[\, {\mathcal{C}}\bigl(\Gamma^{(i^\prime, j^\prime)}_{2k-1},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr], \end{align}
\begin{align}\mathbb{V}ar(S_n^{(\gamma)}) &= \sum_{\ell =1}^k \mathbb{E}( I_\ell ) \geq \mathbb{E} ( I_1 ) \geq E\Bigl[\, {\mathcal{C}}\bigl(\Gamma^{(i^\prime, j^\prime)}_{2k-1},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr], \end{align}
where
![]() $i^\prime = j^\prime = (k)$
, that is,
$i^\prime = j^\prime = (k)$
, that is,
![]() $d_{i^\prime} = d_{j^\prime} = d_{(k)}$
. Therefore, applying Theorem 1 to (38), we derive that
$d_{i^\prime} = d_{j^\prime} = d_{(k)}$
. Therefore, applying Theorem 1 to (38), we derive that
 \begin{equation} \mathbb{V}ar(S_n^{(\gamma)}) = \Omega \Bigg(n^{2k-1} e^{-\zeta(d-1) (k-1)R_n} a_n^{(\gamma)} (2 d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)} (d_{(i)})^2\Bigg).\end{equation}
\begin{equation} \mathbb{V}ar(S_n^{(\gamma)}) = \Omega \Bigg(n^{2k-1} e^{-\zeta(d-1) (k-1)R_n} a_n^{(\gamma)} (2 d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)} (d_{(i)})^2\Bigg).\end{equation}
Note that owing to (32) and (34), the assumption
![]() $\gamma \neq 1/2$
is not required for the lower bound. Similarly, by using the bound
$\gamma \neq 1/2$
is not required for the lower bound. Similarly, by using the bound
![]() $I_k \geq {\mathcal{C}}\bigl(\Gamma_k,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)$
and Theorem 1, we get
$I_k \geq {\mathcal{C}}\bigl(\Gamma_k,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)$
and Theorem 1, we get
 \begin{equation} \mathbb{V}ar(S_n^{(\gamma)}) \geq \mathbb{E} ( I_k ) \geq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(\Gamma_k,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr] = O\Bigg( n^k e^{-\zeta(d-1) (k-1)R_n/2} \prod_{i=1}^k a_n^{(\gamma)} (d_i)\Bigg).\end{equation}
\begin{equation} \mathbb{V}ar(S_n^{(\gamma)}) \geq \mathbb{E} ( I_k ) \geq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(\Gamma_k,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr] = O\Bigg( n^k e^{-\zeta(d-1) (k-1)R_n/2} \prod_{i=1}^k a_n^{(\gamma)} (d_i)\Bigg).\end{equation}
Finally, combining (39) and (40) establishes (16).
We now proceed to showing (17). Assume that
![]() $\alpha /\zeta > d_{(k)}$
, and for
$\alpha /\zeta > d_{(k)}$
, and for
![]() $0<\gamma <1$
, write
$0<\gamma <1$
, write
![]() $\mathbb{V}ar(S_n^{(\gamma)}) = \sum_{\ell = 1}^k \mathbb{E}( I_\ell )$
as in (38). To derive exact asymptotics for
$\mathbb{V}ar(S_n^{(\gamma)}) = \sum_{\ell = 1}^k \mathbb{E}( I_\ell )$
as in (38). To derive exact asymptotics for
![]() $\mathbb{V}ar(S_n^{(\gamma)})$
, we need to derive exact asymptotics for
$\mathbb{V}ar(S_n^{(\gamma)})$
, we need to derive exact asymptotics for
![]() $\mathbb{E}( I_1)$
and
$\mathbb{E}( I_1)$
and
![]() $\mathbb{E}( I_k)$
and also show that
$\mathbb{E}( I_k)$
and also show that
![]() $\mathbb{E}(I_{\ell}) = o\bigl(\mathbb{E}( I_1) \vee \mathbb{E}( I_k)\bigr)$
for
$\mathbb{E}(I_{\ell}) = o\bigl(\mathbb{E}( I_1) \vee \mathbb{E}( I_k)\bigr)$
for
![]() $2 \leq \ell \leq k-1$
.
$2 \leq \ell \leq k-1$
.
From the representation of
![]() $I_1$
before (38) and Theorem 1, we have that
$I_1$
before (38) and Theorem 1, we have that
 \begin{align*}\mathbb{E} ( I_1 ) &= \sum_{i,j=1}^k \, \mathbb{E} \Bigl[ \, {\mathcal{C}}\bigl(\Gamma^{(i,j)}_{2k-1},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr) \Bigr] \\&\sim C^* n^{2k-1} e^{-\zeta(d-1) (k-1)R_n} \sum_{i,j=1}^k \prod_{\ell = 1, \, \ell \neq i,j}^k a_n^{(\gamma)} (d_\ell)^2 a_n^{(\gamma)} (d_i+d_j) a_n^{(\gamma)}(d_i) a_n^{(\gamma)} (d_j).\end{align*}
\begin{align*}\mathbb{E} ( I_1 ) &= \sum_{i,j=1}^k \, \mathbb{E} \Bigl[ \, {\mathcal{C}}\bigl(\Gamma^{(i,j)}_{2k-1},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr) \Bigr] \\&\sim C^* n^{2k-1} e^{-\zeta(d-1) (k-1)R_n} \sum_{i,j=1}^k \prod_{\ell = 1, \, \ell \neq i,j}^k a_n^{(\gamma)} (d_\ell)^2 a_n^{(\gamma)} (d_i+d_j) a_n^{(\gamma)}(d_i) a_n^{(\gamma)} (d_j).\end{align*}
However, because of the constraint
![]() $\alpha /\zeta > d_{(k)} $
, we see that
$\alpha /\zeta > d_{(k)} $
, we see that
 \begin{align*}\prod_{\ell = 1, \, \ell \neq i,j}^k a_n^{(\gamma)} (d_\ell)^2 a_n^{(\gamma)} (d_i+d_j) a_n^{(\gamma)}(d_i) a_n^{(\gamma)} (d_j)\end{align*}
\begin{align*}\prod_{\ell = 1, \, \ell \neq i,j}^k a_n^{(\gamma)} (d_\ell)^2 a_n^{(\gamma)} (d_i+d_j) a_n^{(\gamma)}(d_i) a_n^{(\gamma)} (d_j)\end{align*}
tends to a positive constant for all
![]() $i,j = 1,\dots,k$
. Thus, we conclude that
$i,j = 1,\dots,k$
. Thus, we conclude that
Similarly, we can verify that
![]() $\mathbb{E}(I_k) \sim C^* n^{k} e^{-\zeta (d-1) (k-1)R_n/2} \ \ \text{as } n\to\infty$
.
$\mathbb{E}(I_k) \sim C^* n^{k} e^{-\zeta (d-1) (k-1)R_n/2} \ \ \text{as } n\to\infty$
.
Next we investigate the rate of
![]() $\mathbb{E}(I_\ell)$
for
$\mathbb{E}(I_\ell)$
for
![]() $\ell =2,\ldots,k-1$
. Similarly to
$\ell =2,\ldots,k-1$
. Similarly to
![]() $I_1$
, we can express
$I_1$
, we can express
![]() $I_\ell$
as a sum of
$I_\ell$
as a sum of
![]() ${\mathcal{C}}\bigl(H,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)$
over subgraphs H on
${\mathcal{C}}\bigl(H,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)$
over subgraphs H on
![]() $[2k-\ell]$
formed by identifying
$[2k-\ell]$
formed by identifying
![]() $\ell$
vertices on two copies of
$\ell$
vertices on two copies of
![]() $\Gamma_k$
. Choosing a spanning tree
$\Gamma_k$
. Choosing a spanning tree
![]() $\Gamma_H$
of H, and using the monotonicity of
$\Gamma_H$
of H, and using the monotonicity of
![]() ${\mathcal{C}}$
, we get
${\mathcal{C}}$
, we get
![]() ${\mathcal{C}}\bigl(H,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr) \leq {\mathcal{C}}\bigl(\Gamma_H,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)$
; see Figure 4(c)–(d). By the choice of H and
${\mathcal{C}}\bigl(H,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr) \leq {\mathcal{C}}\bigl(\Gamma_H,HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)$
; see Figure 4(c)–(d). By the choice of H and
![]() $\Gamma_H$
, the vertex degrees are necessarily smaller than
$\Gamma_H$
, the vertex degrees are necessarily smaller than
![]() $\alpha / \zeta$
. Thus, from Theorem 1, we get that for every
$\alpha / \zeta$
. Thus, from Theorem 1, we get that for every
![]() $\Gamma_H$
,
$\Gamma_H$
,
Now, we derive that
Note that for every
![]() $n\geq1$
,
$n\geq1$
,
![]() $g(m) = n^m e^{-\zeta(d-1)(m-1)R_n/2}$
is monotonic in
$g(m) = n^m e^{-\zeta(d-1)(m-1)R_n/2}$
is monotonic in
![]() $m \in {\mathbb N}_+$
, so either
$m \in {\mathbb N}_+$
, so either
![]() $\mathbb{E}( I_1 )$
or
$\mathbb{E}( I_1 )$
or
![]() $\mathbb{E} ( I_k )$
determines the actual growth rate of
$\mathbb{E} ( I_k )$
determines the actual growth rate of
![]() $\mathbb{V}ar(S_n^{(\gamma)})$
. Thus, we have that
$\mathbb{V}ar(S_n^{(\gamma)})$
. Thus, we have that
![]() $\mathbb{E}(I_\ell) = o\bigl(\mathbb{E}( I_1) \vee \mathbb{E}( I_k)\bigr)$
for all
$\mathbb{E}(I_\ell) = o\bigl(\mathbb{E}( I_1) \vee \mathbb{E}( I_k)\bigr)$
for all
![]() $2 \leq \ell \leq k-1$
, and we can conclude that
$2 \leq \ell \leq k-1$
, and we can conclude that
Next, let
![]() $U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
for
$U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
for
![]() $0 < \gamma <1$
. We can finish the proof provided that
$0 < \gamma <1$
. We can finish the proof provided that
As in the proof for
![]() $\mathbb{V}ar(S_n^{(\gamma)})$
, we write
$\mathbb{V}ar(S_n^{(\gamma)})$
, we write
 \begin{align*}\mathbb{V}ar(U_n^{(\gamma)}) &= \, \sum_{\ell=1}^k\mathbb{E} \Bigg[ \sum_{(X_1,\dots,X_{2k-\ell}) \in \mathcal P_{n,\neq}^{2k-\ell}} h_{n,\gamma} (X_1,\dots,X_k)\, \\&\qquad \qquad\qquad\qquad \times h_{n,\gamma}(X_1,\dots,X_\ell,X_{k+1},\dots,X_{2k-\ell}) \Bigg] \,{=\!:}\, \sum_{\ell=1}^k \mathbb{E}( J_\ell ).\end{align*}
\begin{align*}\mathbb{V}ar(U_n^{(\gamma)}) &= \, \sum_{\ell=1}^k\mathbb{E} \Bigg[ \sum_{(X_1,\dots,X_{2k-\ell}) \in \mathcal P_{n,\neq}^{2k-\ell}} h_{n,\gamma} (X_1,\dots,X_k)\, \\&\qquad \qquad\qquad\qquad \times h_{n,\gamma}(X_1,\dots,X_\ell,X_{k+1},\dots,X_{2k-\ell}) \Bigg] \,{=\!:}\, \sum_{\ell=1}^k \mathbb{E}( J_\ell ).\end{align*}
Repeating the same argument as in the proof of (37) in Theorem 1, we obtain that for all
![]() $\ell=1,\dots,k$
,
$\ell=1,\dots,k$
,
Thus, (41) follows. Moreover, by the Cauchy–Schwarz inequality,
from which we have
 \begin{align*}\mathbb{V}ar(S_n) &= \mathbb{V}ar(S_n^{(\gamma)}) + \mathbb{V}ar(U_n^{(\gamma)}) +2\text{Cov}(S_n^{(\gamma)},U_n^{(\gamma)}) \\&\sim C^*\Bigl[ n^{2k-1}e^{-\zeta(d-1)(k-1)R_n} \vee n^k e^{-\zeta(d-1) (k-1)R_n/2} \Bigr], \, \, \, n\to\infty.\\[-35pt]\end{align*}
\begin{align*}\mathbb{V}ar(S_n) &= \mathbb{V}ar(S_n^{(\gamma)}) + \mathbb{V}ar(U_n^{(\gamma)}) +2\text{Cov}(S_n^{(\gamma)},U_n^{(\gamma)}) \\&\sim C^*\Bigl[ n^{2k-1}e^{-\zeta(d-1)(k-1)R_n} \vee n^k e^{-\zeta(d-1) (k-1)R_n/2} \Bigr], \, \, \, n\to\infty.\\[-35pt]\end{align*}
3.3. Proof of the central limit theorem
The proof relies on the normal approximation bound derived from the Malliavin–Stein method in [Reference Last, Peccati and Schulte32] (see Theorem 4 below). The Malliavin–Stein method has emerged as a crucial tool for the approximation of Gaussian, Poisson, and Rademacher functionals. An important aspect of the method is to express the terms in Stein’s equation in terms of the Malliavin operators and derive suitable estimates for the latter. The bound in [Reference Last, Peccati and Schulte32] reduces estimates involving the Malliavin operators to those expressed in terms of more tractable difference operators. For a more detailed introduction to this subject, see [Reference Last and Penrose33, Reference Peccati and Reitzner37]. In our proof, we use only the first- and second-order difference operators. Our sub-tree counts are U-statistics, and one may express these difference operators in terms of
![]() $g_{n,\gamma}$
as defined in (30). The bulk of our work (see Lemmas 5–7) will be in deducing good estimates for these difference operators. By substituting the obtained estimates and the already derived variance estimates into the second-order Poincaré inequality, we obtain the required normal approximation.
$g_{n,\gamma}$
as defined in (30). The bulk of our work (see Lemmas 5–7) will be in deducing good estimates for these difference operators. By substituting the obtained estimates and the already derived variance estimates into the second-order Poincaré inequality, we obtain the required normal approximation.
This section is organized as follows. In Section 3.3.1 we introduce the normal approximation bound, as well as simplifications for our case. Next, in Section 3.3.2 we derive necessary estimates for difference operators, which we use in Section 3.3.3 to complete the proof of the CLT.
3.3.1. Malliavin–Stein bound for Poisson functionals
Let
![]() $\mathcal{P}$
be a Poisson point process on a finite measure space X with intensity measure
$\mathcal{P}$
be a Poisson point process on a finite measure space X with intensity measure
![]() $\lambda(\cdot)$
. For a functional F of Radon counting measures (i.e., locally finite collection of points), define the Malliavin difference operators as follows. For
$\lambda(\cdot)$
. For a functional F of Radon counting measures (i.e., locally finite collection of points), define the Malliavin difference operators as follows. For
![]() $x \in {\textbf{X}}$
, the first-order difference operator is
$x \in {\textbf{X}}$
, the first-order difference operator is
![]() $D_xF \,{:\!=}\, F(\mathcal{P} \cup \{x\}) - F(\mathcal{P})$
. The higher-order difference operators are defined inductively as
$D_xF \,{:\!=}\, F(\mathcal{P} \cup \{x\}) - F(\mathcal{P})$
. The higher-order difference operators are defined inductively as
![]() $D^\ell_{x_1,\ldots,x_\ell} F\,{:\!=}\, D_{x_\ell}(D^{\ell-1}_{x_1,\ldots,x_{\ell-1}}F)$
. We require only the first- and second-order difference operators. The latter is easily seen to be
$D^\ell_{x_1,\ldots,x_\ell} F\,{:\!=}\, D_{x_\ell}(D^{\ell-1}_{x_1,\ldots,x_{\ell-1}}F)$
. We require only the first- and second-order difference operators. The latter is easily seen to be
for
![]() $x,y \in {\textbf{X}}$
. We say that
$x,y \in {\textbf{X}}$
. We say that
![]() $F \in dom \, D$
if
$F \in dom \, D$
if
The normal approximation bounds in [Reference Last, Peccati and Schulte32, Theorems 1.1 and 1.2] are given in a compact form but involve the second moments of the product of second-order difference operators. A simplified version of [Reference Last, Peccati and Schulte32, Theorems 1.1 and 1.2] is given in [Reference Last, Peccati and Schulte32, Proposition 1.4], but it does not suffice for our purposes. Therefore, the bounds we shall use below are those obtained by combining [Reference Last, Peccati and Schulte32, Theorems 1.1 and 1.2] and [Reference Last, Peccati and Schulte32, Theorem 6.1].
Theorem 4. ([Reference Last, Peccati and Schulte32, Theorems 1.1, 1.2, and 6.1]) Let
![]() $F \in dom \, D$
and let N be a standard normal random variable. Define
$F \in dom \, D$
and let N be a standard normal random variable. Define
where these supremums are essential supremums with respect to
![]() $\lambda$
and
$\lambda$
and
![]() $\lambda^2$
, respectively. Then
$\lambda^2$
, respectively. Then
 \begin{eqnarray*}d_W\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & W_1 + W_2 + W_3, \\[3pt]d_K\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & W_1 + W_2 + W_3 + W_4 + W_5 + W_6,\end{eqnarray*}
\begin{eqnarray*}d_W\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & W_1 + W_2 + W_3, \\[3pt]d_K\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & W_1 + W_2 + W_3 + W_4 + W_5 + W_6,\end{eqnarray*}
where
![]() $W_1,\dots,W_6$
are defined as follows:
$W_1,\dots,W_6$
are defined as follows:
 \begin{align*}W_1 & = \frac{2(c_1c_2)^{1/5}}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^3} \left[ \mathbb{P}\left(D^2_{x_1,x_3}F \neq 0\right)\mathbb{P}\left(D^2_{x_2,x_3}F \neq 0\right) \right]^{1/20} \lambda^3\bigl(\mathrm{d} (x_1,x_2,x_3)\bigr) \right]^{1/2}, \\[3pt]W_2 & = \frac{c_2^{2/5}}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^3} \left[ \mathbb{P}\left(D^2_{x_1,x_3}F \neq 0\right)\mathbb{P}\left(D^2_{x_2,x_3}F \neq 0\right) \right]^{1/10} \lambda^3\bigl(\mathrm{d} (x_1,x_2,x_3)\bigr) \right]^{1/2}, \\[3pt]W_3 & = \frac{1}{\mathbb{V}ar(F)^{3/2}} \int_{\textbf{X}} \mathbb{E}\bigl(|D_xF|^3\bigr) \lambda(\mathrm{d} x), \\[3pt]W_4 & = \frac{c_1^{3/5}\lambda({\textbf{X}})}{\mathbb{V}ar(F)^{3/2}} + \frac{c_1^{4/5}\lambda({\textbf{X}})^{5/4} + 2 c_1^{4/5}\lambda({\textbf{X}})^{3/2}}{\mathbb{V}ar(F)^2}, \\[3pt]W_5 & = \frac{c_1^{2/5}\lambda({\textbf{X}})^{1/2}}{\mathbb{V}ar(F)}, \\[3pt]W_6 & = \frac{ \sqrt{6}(c_1c_2)^{1/5} + \sqrt{3}c_2^{2/5}}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^2} \mathbb{P}(D^2_{x_1,x_2}F \neq 0) ]^{1/10} \lambda^2\bigl(\mathrm{d} (x_1,x_2)\bigr) \right]^{1/2}.\end{align*}
\begin{align*}W_1 & = \frac{2(c_1c_2)^{1/5}}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^3} \left[ \mathbb{P}\left(D^2_{x_1,x_3}F \neq 0\right)\mathbb{P}\left(D^2_{x_2,x_3}F \neq 0\right) \right]^{1/20} \lambda^3\bigl(\mathrm{d} (x_1,x_2,x_3)\bigr) \right]^{1/2}, \\[3pt]W_2 & = \frac{c_2^{2/5}}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^3} \left[ \mathbb{P}\left(D^2_{x_1,x_3}F \neq 0\right)\mathbb{P}\left(D^2_{x_2,x_3}F \neq 0\right) \right]^{1/10} \lambda^3\bigl(\mathrm{d} (x_1,x_2,x_3)\bigr) \right]^{1/2}, \\[3pt]W_3 & = \frac{1}{\mathbb{V}ar(F)^{3/2}} \int_{\textbf{X}} \mathbb{E}\bigl(|D_xF|^3\bigr) \lambda(\mathrm{d} x), \\[3pt]W_4 & = \frac{c_1^{3/5}\lambda({\textbf{X}})}{\mathbb{V}ar(F)^{3/2}} + \frac{c_1^{4/5}\lambda({\textbf{X}})^{5/4} + 2 c_1^{4/5}\lambda({\textbf{X}})^{3/2}}{\mathbb{V}ar(F)^2}, \\[3pt]W_5 & = \frac{c_1^{2/5}\lambda({\textbf{X}})^{1/2}}{\mathbb{V}ar(F)}, \\[3pt]W_6 & = \frac{ \sqrt{6}(c_1c_2)^{1/5} + \sqrt{3}c_2^{2/5}}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^2} \mathbb{P}(D^2_{x_1,x_2}F \neq 0) ]^{1/10} \lambda^2\bigl(\mathrm{d} (x_1,x_2)\bigr) \right]^{1/2}.\end{align*}
For a self-contained proof, we state [Reference Last, Peccati and Schulte32, Theorems 1.1 and 1.2] in the appendix, explaining how the above theorem can be deduced using the proof strategy of [Reference Last, Peccati and Schulte32, Theorem 6.1].
In order to apply Theorem 4 to our setup, we take
where x is represented by its hyperbolic polar coordinates
![]() $(t,\theta)$
.
$(t,\theta)$
.
In what follows, we write
![]() $g = g_{n,\gamma}$
(see (30)). Observe that
$g = g_{n,\gamma}$
(see (30)). Observe that
![]() $S_n^{(\gamma)}$
is a U-statistic and its Malliavin derivatives have a neat form as follows: for two distinct points
$S_n^{(\gamma)}$
is a U-statistic and its Malliavin derivatives have a neat form as follows: for two distinct points
![]() $x, y \in B_d^{(\zeta)}$
,
$x, y \in B_d^{(\zeta)}$
,
 \begin{align}D_{x}S_n^{(\gamma)} &= \sum_{\ell =1}^k \sum_{(X_1,\ldots, X_{k-1}) \in \mathcal{P}^{k-1}_{n,\neq}}g(\underset{ \ell}{X_1,\ldots,x,\ldots, X_{k-1}}), \end{align}
\begin{align}D_{x}S_n^{(\gamma)} &= \sum_{\ell =1}^k \sum_{(X_1,\ldots, X_{k-1}) \in \mathcal{P}^{k-1}_{n,\neq}}g(\underset{ \ell}{X_1,\ldots,x,\ldots, X_{k-1}}), \end{align}
where
![]() $\ell$
and the
$\ell$
and the
![]() $\ell_i$
denote the positions of the corresponding coordinates. In particular, (42) represents the number of injective homomorphisms from
$\ell_i$
denote the positions of the corresponding coordinates. In particular, (42) represents the number of injective homomorphisms from
![]() $\Gamma_k$
to
$\Gamma_k$
to
![]() $HG_n^{(\gamma)}(R_n;\ \alpha, \zeta)$
, with one of its vertices fixed at x and the remaining
$HG_n^{(\gamma)}(R_n;\ \alpha, \zeta)$
, with one of its vertices fixed at x and the remaining
![]() $k-1$
points taken from
$k-1$
points taken from
![]() $\mathcal{P}_n$
. Similarly, (43) represents the number of injective homomorphisms, but here, two of the vertices are fixed at x and y, respectively.
$\mathcal{P}_n$
. Similarly, (43) represents the number of injective homomorphisms, but here, two of the vertices are fixed at x and y, respectively.
From (42) and (43), the constants
![]() $c_1$
,
$c_1$
,
![]() $c_2$
in Theorem 4 have become
$c_2$
in Theorem 4 have become
For notational convenience later on, we also define
where x is again represented by its hyperbolic polar coordinates
![]() $(t,\theta)$
. With this notation and the preliminary facts now available, we can rephrase
$(t,\theta)$
. With this notation and the preliminary facts now available, we can rephrase
![]() $W_i$
,
$W_i$
,
![]() $i=1,\dots,6$
, in Theorem 4 as follows:
$i=1,\dots,6$
, in Theorem 4 as follows:
 \begin{align}W_1 &= \frac{2n^{3/2}(c_{1,n}c_{2,n})^{1/5}}{\mathbb{V}ar(S_n^{(\gamma)})}\nonumber\\ &\quad \times \Bigg[ \int_{[0,\gamma R_n]^3 \times C_d^3} [\mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0) ]^{1/20} \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \Bigg]^{1/2}, \nonumber \\W_2 &= \frac{n^{3/2}(c_{2,n})^{2/5}}{\mathbb{V}ar(S_n^{(\gamma)})} \nonumber\\[3pt] &\quad \times \Bigg[ \int_{[0,\gamma R_n]^3 \times C_d^3} [\mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0) ]^{1/10} \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \Bigg]^{1/2}, \nonumber\\W_3 &= \frac{n c_{3,n}}{\mathbb{V}ar(S_n^{(\gamma)})^{3/2}}, \nonumber \\W_4 &= \frac{n(c_{1,n})^{3/5}}{\mathbb{V}ar(S_n^{(\gamma)})^{3/2}} + \frac{n^{5/4}(c_{1,n})^{4/5} + 2 n^{3/2} (c_{1,n})^{4/5}}{\mathbb{V}ar(S_n^{(\gamma)})^2}, \nonumber \\W_5 &= \frac{n^{1/2}(c_{1,n})^{2/5}}{\mathbb{V}ar(S_n^{(\gamma)})}, \nonumber \\W_6 &= \frac{ n \big\{ \sqrt{6}(c_{1,n}c_{2,n})^{1/5} + \sqrt{3}(c_{2,n})^{2/5} \big\}}{\mathbb{V}ar(S_n^{(\gamma)})}\nonumber\\[3pt] &\quad \times \Bigg[ \int_{[0,\gamma R_n]^2 \times C_d^2} [ \mathbb{P}(D^2_{x_1,x_2}S_n^{(\gamma)} \neq 0)]^{1/10} \prod_{i=1}^2\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \Bigg]^{1/2},\end{align}
\begin{align}W_1 &= \frac{2n^{3/2}(c_{1,n}c_{2,n})^{1/5}}{\mathbb{V}ar(S_n^{(\gamma)})}\nonumber\\ &\quad \times \Bigg[ \int_{[0,\gamma R_n]^3 \times C_d^3} [\mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0) ]^{1/20} \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \Bigg]^{1/2}, \nonumber \\W_2 &= \frac{n^{3/2}(c_{2,n})^{2/5}}{\mathbb{V}ar(S_n^{(\gamma)})} \nonumber\\[3pt] &\quad \times \Bigg[ \int_{[0,\gamma R_n]^3 \times C_d^3} [\mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0) ]^{1/10} \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \Bigg]^{1/2}, \nonumber\\W_3 &= \frac{n c_{3,n}}{\mathbb{V}ar(S_n^{(\gamma)})^{3/2}}, \nonumber \\W_4 &= \frac{n(c_{1,n})^{3/5}}{\mathbb{V}ar(S_n^{(\gamma)})^{3/2}} + \frac{n^{5/4}(c_{1,n})^{4/5} + 2 n^{3/2} (c_{1,n})^{4/5}}{\mathbb{V}ar(S_n^{(\gamma)})^2}, \nonumber \\W_5 &= \frac{n^{1/2}(c_{1,n})^{2/5}}{\mathbb{V}ar(S_n^{(\gamma)})}, \nonumber \\W_6 &= \frac{ n \big\{ \sqrt{6}(c_{1,n}c_{2,n})^{1/5} + \sqrt{3}(c_{2,n})^{2/5} \big\}}{\mathbb{V}ar(S_n^{(\gamma)})}\nonumber\\[3pt] &\quad \times \Bigg[ \int_{[0,\gamma R_n]^2 \times C_d^2} [ \mathbb{P}(D^2_{x_1,x_2}S_n^{(\gamma)} \neq 0)]^{1/10} \prod_{i=1}^2\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \Bigg]^{1/2},\end{align}
where we identify the terms
![]() $x_i$
with their hyperbolic polar coordinates
$x_i$
with their hyperbolic polar coordinates
![]() $(t_i, \theta_i)$
.
$(t_i, \theta_i)$
.
3.3.2. Some auxiliary lemmas for the proof of the central limit theorem
Having already derived variance bounds in Theorem 2, we now deduce necessary estimates for the
![]() $W_i$
terms in (44). More specifically, Lemmas 5 and 6 below are used to estimate
$W_i$
terms in (44). More specifically, Lemmas 5 and 6 below are used to estimate
![]() $c_{1,n}$
,
$c_{1,n}$
,
![]() $c_{2,n}$
, and
$c_{2,n}$
, and
![]() $c_{3,n}$
, while Lemma 7 calculates the rate of the remaining integral terms. These estimates are then substituted into the
$c_{3,n}$
, while Lemma 7 calculates the rate of the remaining integral terms. These estimates are then substituted into the
![]() $W_i$
terms in (44). Recall that
$W_i$
terms in (44). Recall that
![]() $C^*$
is a positive generic constant, which is independent of n.
$C^*$
is a positive generic constant, which is independent of n.
Lemma 5. Let the assumptions of Theorem 3 hold, and let
![]() $\gamma \in (0,1/2)$
. Set
$\gamma \in (0,1/2)$
. Set
![]() $\rho_n \,{:\!=}\, ne^{-\zeta(d-1) R_n/2}.$
For
$\rho_n \,{:\!=}\, ne^{-\zeta(d-1) R_n/2}.$
For
![]() $p \geq 1$
, define
$p \geq 1$
, define
![]() $\mathcal{G}_p^{(1)}$
and
$\mathcal{G}_p^{(1)}$
and
![]() $\mathcal{G}_p^{(2)}$
respectively to be the set of all trees on
$\mathcal{G}_p^{(2)}$
respectively to be the set of all trees on
![]() $\{0\} \cup [p]$
and
$\{0\} \cup [p]$
and
![]() $\{-1,0\} \cup [p]$
. For a tree
$\{-1,0\} \cup [p]$
. For a tree
![]() $T \in \mathcal{G}_p^{(1)}$
, let
$T \in \mathcal{G}_p^{(1)}$
, let
![]() $d^{\prime}_0, d^{\prime}_1,\ldots, d^{\prime}_p$
be the degree sequence, and similarly, for a tree
$d^{\prime}_0, d^{\prime}_1,\ldots, d^{\prime}_p$
be the degree sequence, and similarly, for a tree
![]() $T \in \mathcal{G}_p^{(2)}$
, let
$T \in \mathcal{G}_p^{(2)}$
, let
![]() $d^{\prime}_{-1},d^{\prime}_0,\ldots,d^{\prime}_p$
be the degree sequence. Then we have
$d^{\prime}_{-1},d^{\prime}_0,\ldots,d^{\prime}_p$
be the degree sequence. Then we have
where
 \begin{align*}c^{\prime}_{1,n}&\,{:\!=}\, \max_{\substack{p = k-1,\ldots,5(k-1), \\[3pt] T \in \mathcal{G}_p^{(1)}}} e^{\zeta (d-1) d_0^\prime \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i), \\c^{\prime}_{2,n} &\,{:\!=}\, \max_{\substack{p = k-2,\ldots,5(k-2), \\ T \in \mathcal{G}_p^{(2)}}}e^{\zeta (d-1)(d_{-1}^{\prime} + d_0^{\prime})\gamma R_n/2}\prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i).\end{align*}
\begin{align*}c^{\prime}_{1,n}&\,{:\!=}\, \max_{\substack{p = k-1,\ldots,5(k-1), \\[3pt] T \in \mathcal{G}_p^{(1)}}} e^{\zeta (d-1) d_0^\prime \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i), \\c^{\prime}_{2,n} &\,{:\!=}\, \max_{\substack{p = k-2,\ldots,5(k-2), \\ T \in \mathcal{G}_p^{(2)}}}e^{\zeta (d-1)(d_{-1}^{\prime} + d_0^{\prime})\gamma R_n/2}\prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i).\end{align*}
Lemma 6. In the notation of Lemma 5, for
![]() $0 < \gamma < 1/2$
,
$0 < \gamma < 1/2$
,
where
 \begin{align*}c^{\prime}_{3,n} \,{:\!=}\, \max_{\substack{p = k-1,\ldots,3(k-1), \\ T \in \mathcal{G}_p^{(1)}}} \prod_{i=0}^p a_n^{(\gamma)}(d^{\prime}_i).\end{align*}
\begin{align*}c^{\prime}_{3,n} \,{:\!=}\, \max_{\substack{p = k-1,\ldots,3(k-1), \\ T \in \mathcal{G}_p^{(1)}}} \prod_{i=0}^p a_n^{(\gamma)}(d^{\prime}_i).\end{align*}
Lemma 7. For
![]() $0 < \gamma < 1/2$
and
$0 < \gamma < 1/2$
and
![]() $0 < a < 1$
, we have
$0 < a < 1$
, we have
 \begin{align*}& \int_{[0,\gamma R_n]^3 \times C_d^3} \left[ \mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}\left(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0\right) \right]^a\\[3pt] &\qquad\times \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i = O\bigl( e^{-\zeta(d-1)(1-2\gamma)R_n}\bigr), \\& \int_{[0,\gamma R_n]^2 \times C_d^2} [ \mathbb{P}(D^2_{x_1,x_2}S_n^{(\gamma)} \neq 0)]^a \prod_{i=1}^2\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i = O\bigl( e^{-\zeta(d-1)(1-2\gamma)R_n/2}\bigr).\end{align*}
\begin{align*}& \int_{[0,\gamma R_n]^3 \times C_d^3} \left[ \mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}\left(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0\right) \right]^a\\[3pt] &\qquad\times \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i = O\bigl( e^{-\zeta(d-1)(1-2\gamma)R_n}\bigr), \\& \int_{[0,\gamma R_n]^2 \times C_d^2} [ \mathbb{P}(D^2_{x_1,x_2}S_n^{(\gamma)} \neq 0)]^a \prod_{i=1}^2\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i = O\bigl( e^{-\zeta(d-1)(1-2\gamma)R_n/2}\bigr).\end{align*}
Remark 3.
-
(i) One can make the growth rate of the
 $c_{i,n}^{\prime}$
as slow as one likes by choosing
$c_{i,n}^{\prime}$
as slow as one likes by choosing
 $\gamma$
small enough. To make this a little more clear, assume, for simplicity, that
$\gamma$
small enough. To make this a little more clear, assume, for simplicity, that
 $2\alpha /\zeta$
is not an integer. Then, as
$2\alpha /\zeta$
is not an integer. Then, as
 $n\to\infty$
, Note also that
$n\to\infty$
, Note also that \begin{align*}c_{1,n}^\prime \sim \max_{\substack{p = k-1,\ldots,5(k-1), \\ T \in \mathcal{G}_p^{(1)}}} \prod_{j=1}^p\, \Bigl| \, (d-1) (\alpha-\zeta d_j^{\prime}/2) \, \Bigr|^{-1} e^{\zeta (d-1)\bigl[ d_0^\prime + \sum_{i=1}^p \bigl( d_i^\prime -2\alpha /\zeta \bigr)_+ \bigr] \gamma R_n /2}.\end{align*}
\begin{align*}c_{1,n}^\prime \sim \max_{\substack{p = k-1,\ldots,5(k-1), \\ T \in \mathcal{G}_p^{(1)}}} \prod_{j=1}^p\, \Bigl| \, (d-1) (\alpha-\zeta d_j^{\prime}/2) \, \Bigr|^{-1} e^{\zeta (d-1)\bigl[ d_0^\prime + \sum_{i=1}^p \bigl( d_i^\prime -2\alpha /\zeta \bigr)_+ \bigr] \gamma R_n /2}.\end{align*}
 $\rho_n\to c \in (0,\infty]$
implies
$\rho_n\to c \in (0,\infty]$
implies
 $R_n = O (\log n)$
. Therefore, for any
$R_n = O (\log n)$
. Therefore, for any
 $\epsilon >0$
, there exists
$\epsilon >0$
, there exists
 $\gamma_0>0$
such that for all
$\gamma_0>0$
such that for all
 $0<\gamma<\gamma_0$
, we have that
$0<\gamma<\gamma_0$
, we have that
 $c_{1,n}^{\prime} = o(n^\epsilon)$
. The same claim holds for
$c_{1,n}^{\prime} = o(n^\epsilon)$
. The same claim holds for
 $c_{2,n}^{\prime}, c_{3,n}^{\prime}$
as well.
$c_{2,n}^{\prime}, c_{3,n}^{\prime}$
as well.
-
(ii) The separation of each
 $c_{i,n}$
into
$c_{i,n}$
into
 $c^{\prime}_{i,n}$
and
$c^{\prime}_{i,n}$
and
 $\rho_n$
terms is because
$\rho_n$
terms is because
 $c^{\prime}_{i,n}$
depends on
$c^{\prime}_{i,n}$
depends on
 $\gamma$
, whereas
$\gamma$
, whereas
 $\rho_n$
does not.
$\rho_n$
does not. -
(iii) In many applications to Euclidean stochastic geometric functionals (see [Reference Last, Peccati and Schulte32, Section 7]),
 $c_{1,n},c_{2.n}$
are shown to be bounded in n, whereas in our case,
$c_{1,n},c_{2.n}$
are shown to be bounded in n, whereas in our case,
 $c_{1,n},c_{2.n}$
are unbounded in n. This is why it is challenging to obtain optimal Berry–Esseen bounds in our normal approximation result.
$c_{1,n},c_{2.n}$
are unbounded in n. This is why it is challenging to obtain optimal Berry–Esseen bounds in our normal approximation result.
Proof of Lemma 5. Fix
![]() $x \in B_d^{(\zeta)}$
. For
$x \in B_d^{(\zeta)}$
. For
![]() $p=k-1,\dots,5(k-1)$
, let
$p=k-1,\dots,5(k-1)$
, let
![]() $\Sigma_{5(k-1),p}$
denote the set of all surjective maps from
$\Sigma_{5(k-1),p}$
denote the set of all surjective maps from
![]() $[5(k-1)]$
to [p]. From (42), we have that
$[5(k-1)]$
to [p]. From (42), we have that
 \begin{align*}&\bigl| D_{x}S_n^{(\gamma)}\bigr|^5 \leq C^* \sum_{\ell =1}^k \Bigg(\sum_{(X_1,\ldots, X_{k-1}) \in \mathcal{P}^{k-1}_{n,\neq}}g(\underset{\ell}{X_1,\ldots,x,\ldots, X_{k-1}})\Bigg)^5 \\&\qquad \quad = C^* \sum_{\ell =1}^k \sum_{p=k-1}^{5(k-1)} \frac{1}{p!}\sum_{\sigma \in \Sigma_{5(k-1),p}}\sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}}\\[3pt] &\qquad\quad \times \prod_{i=1}^5g\bigl(\underset{\ell}{X_{\sigma((i-1)(k-1)+1)},\ldots,x,\ldots, X_{\sigma(i(k-1))}}\bigr).\end{align*}
\begin{align*}&\bigl| D_{x}S_n^{(\gamma)}\bigr|^5 \leq C^* \sum_{\ell =1}^k \Bigg(\sum_{(X_1,\ldots, X_{k-1}) \in \mathcal{P}^{k-1}_{n,\neq}}g(\underset{\ell}{X_1,\ldots,x,\ldots, X_{k-1}})\Bigg)^5 \\&\qquad \quad = C^* \sum_{\ell =1}^k \sum_{p=k-1}^{5(k-1)} \frac{1}{p!}\sum_{\sigma \in \Sigma_{5(k-1),p}}\sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}}\\[3pt] &\qquad\quad \times \prod_{i=1}^5g\bigl(\underset{\ell}{X_{\sigma((i-1)(k-1)+1)},\ldots,x,\ldots, X_{\sigma(i(k-1))}}\bigr).\end{align*}
It is possible that under some surjections
![]() $\sigma$
, the coordinates in
$\sigma$
, the coordinates in
![]() $\bigl(\sigma((i-1)(k-1)+1),\ldots,\sigma(i(k-1))\bigr)$
may repeat for some i, but in such cases,
$\bigl(\sigma((i-1)(k-1)+1),\ldots,\sigma(i(k-1))\bigr)$
may repeat for some i, but in such cases,
![]() $g = 0$
by definition; thus,
$g = 0$
by definition; thus,
![]() $\Sigma_{5(k-1), p}$
in the last expression can be replaced with
$\Sigma_{5(k-1), p}$
in the last expression can be replaced with
 \begin{align*}\Sigma_{5(k-1),p}^* &= \bigl\{\sigma \in \Sigma_{5(k-1), p}: \sigma((i-1)(k-1)+1),\ldots,\sigma(i(k-1))\\[3pt]&\qquad \text{ are distinct for all } i=1,\dots,5 \bigr\}.\end{align*}
\begin{align*}\Sigma_{5(k-1),p}^* &= \bigl\{\sigma \in \Sigma_{5(k-1), p}: \sigma((i-1)(k-1)+1),\ldots,\sigma(i(k-1))\\[3pt]&\qquad \text{ are distinct for all } i=1,\dots,5 \bigr\}.\end{align*}
Now, let us fix
![]() $\ell = 1$
, without loss of generality, and
$\ell = 1$
, without loss of generality, and
![]() $p \in \{k-1,\ldots,5(k-1)\}$
,
$p \in \{k-1,\ldots,5(k-1)\}$
,
![]() $\sigma \in \Sigma_{5(k-1),p}^*$
; then we shall bound
$\sigma \in \Sigma_{5(k-1),p}^*$
; then we shall bound
 \begin{align}A_{n,p,\sigma} \,{:\!=}\, \mathbb{E}\Bigg[ \sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}} \prod_{i=1}^5 g\bigl(x,X_{\sigma((i-1)(k-1)+1)},\ldots, X_{\sigma(i(k-1))} \bigr) \Bigg]. \end{align}
\begin{align}A_{n,p,\sigma} \,{:\!=}\, \mathbb{E}\Bigg[ \sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}} \prod_{i=1}^5 g\bigl(x,X_{\sigma((i-1)(k-1)+1)},\ldots, X_{\sigma(i(k-1))} \bigr) \Bigg]. \end{align}
Let
![]() $G_\sigma$
be a simple graph on
$G_\sigma$
be a simple graph on
![]() $\{0\}\cup [p]$
with the edge set defined as follows: for every
$\{0\}\cup [p]$
with the edge set defined as follows: for every
![]() $i=1,\dots,5$
, define
$i=1,\dots,5$
, define
![]() $\bigl(\sigma((i-1)(k-1)+j_1),\sigma((i-1)(k-1)+j_2) \bigr) \in E_{\sigma}$
if
$\bigl(\sigma((i-1)(k-1)+j_1),\sigma((i-1)(k-1)+j_2) \bigr) \in E_{\sigma}$
if
![]() $(j_1+1,j_2+1)$
is an edge in
$(j_1+1,j_2+1)$
is an edge in
![]() $\Gamma_k$
. Similarly we say that
$\Gamma_k$
. Similarly we say that
![]() $\bigl(0,\sigma((i-1)(k-1)+j)\bigr) \in E_{\sigma}$
if
$\bigl(0,\sigma((i-1)(k-1)+j)\bigr) \in E_{\sigma}$
if
![]() $(1,j+1)$
is an edge in
$(1,j+1)$
is an edge in
![]() $\Gamma_k$
. Then, setting
$\Gamma_k$
. Then, setting
![]() $X_0 = x$
, we have that
$X_0 = x$
, we have that
![]() $G_{\sigma}$
is the graph counted by the summand in (47), i.e.,
$G_{\sigma}$
is the graph counted by the summand in (47), i.e.,
 \begin{equation}\prod_{i=1}^5 g\bigl(x,X_{\sigma((i-1)(k-1)+1)},\ldots, X_{\sigma(i(k-1))} \bigr) = \prod_{(i,j) \in G_{\sigma}}{\textbf{1}} \bigl\{ d_\zeta(X_i,X_j) \leq R_n \bigr\}.\end{equation}
\begin{equation}\prod_{i=1}^5 g\bigl(x,X_{\sigma((i-1)(k-1)+1)},\ldots, X_{\sigma(i(k-1))} \bigr) = \prod_{(i,j) \in G_{\sigma}}{\textbf{1}} \bigl\{ d_\zeta(X_i,X_j) \leq R_n \bigr\}.\end{equation}
Now, the surjectivity of
![]() $\sigma$
implies that
$\sigma$
implies that
![]() $G_\sigma$
is connected, and thus we can always find a spanning tree
$G_\sigma$
is connected, and thus we can always find a spanning tree
![]() $G_{\sigma}^{\prime}$
of
$G_{\sigma}^{\prime}$
of
![]() $G_\sigma$
on
$G_\sigma$
on
![]() $\{ 0\}\cup [p]$
. Let
$\{ 0\}\cup [p]$
. Let
![]() $d_0^{\prime}, \dots, d_p^{\prime}$
be the degree sequence of
$d_0^{\prime}, \dots, d_p^{\prime}$
be the degree sequence of
![]() $G_\sigma^{\prime}$
, and let
$G_\sigma^{\prime}$
, and let
![]() $E^{\prime}_\sigma$
be the edge set of
$E^{\prime}_\sigma$
be the edge set of
![]() $G_\sigma^{\prime}$
. By the definitions of
$G_\sigma^{\prime}$
. By the definitions of
![]() $A_{n,p,\sigma},G_{\sigma}, G^{\prime}_{\sigma}$
, together with the monotonicity of
$A_{n,p,\sigma},G_{\sigma}, G^{\prime}_{\sigma}$
, together with the monotonicity of
![]() ${\mathcal{C}}$
and the above identity, we have that
${\mathcal{C}}$
and the above identity, we have that
 \begin{align}A_{n,p,\sigma} &= \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr]\leq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma}^{\prime},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr] \nonumber\\[3pt]&= n^p \mathbb{P} \bigl(\, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E^{\prime}_\sigma, \ T_i \leq \gamma R_n, \, i=1,\dots,p, \, t_0 \leq \gamma R_n \bigr),\end{align}
\begin{align}A_{n,p,\sigma} &= \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr]\leq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma}^{\prime},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr] \nonumber\\[3pt]&= n^p \mathbb{P} \bigl(\, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E^{\prime}_\sigma, \ T_i \leq \gamma R_n, \, i=1,\dots,p, \, t_0 \leq \gamma R_n \bigr),\end{align}
where
![]() $t_0=R_n-d_\zeta(0,x)$
is deterministic, and the Mecke formula is applied at the last equality. Note that
$t_0=R_n-d_\zeta(0,x)$
is deterministic, and the Mecke formula is applied at the last equality. Note that
![]() $|E^{\prime}_\sigma|=p$
.
$|E^{\prime}_\sigma|=p$
.
Proceeding as in the derivation of (34) and noting that
![]() $T_i+T_j\leq R_n-\omega_n$
with
$T_i+T_j\leq R_n-\omega_n$
with
![]() $\omega_n=\log \log R_n$
always holds as we are taking
$\omega_n=\log \log R_n$
always holds as we are taking
![]() $\gamma<1/2$
, we derive that
$\gamma<1/2$
, we derive that
 \begin{align}A_{n,p,\sigma} &\leq n^p \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_p\, {\textbf{1}} \{ t_0\leq \gamma R_n \} \prod_{(i,j)\in E^{\prime}_\sigma} \mathbb{P} \bigl( d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}} \bigr)\bar \rho_{n,\alpha} ({\textbf{t}}) \nonumber\\&\sim \Bigl( \frac{2^{d-1}}{\kappa_{d-2}} \Bigr)^p\, \alpha^p n^p e^{-\zeta (d-1)p R_n/2} e^{\zeta (d-1) d_0^{\prime} t_0/2}{\textbf{1}} \{ t_0\leq \gamma R_n \}\prod_{i=1}^pa_n^{(\gamma)} (d_i^{\prime}) \notag \\&= O \bigl( \rho_n^p e^{\zeta (d-1) d_0^{\prime} \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \bigr). \end{align}
\begin{align}A_{n,p,\sigma} &\leq n^p \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_p\, {\textbf{1}} \{ t_0\leq \gamma R_n \} \prod_{(i,j)\in E^{\prime}_\sigma} \mathbb{P} \bigl( d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}} \bigr)\bar \rho_{n,\alpha} ({\textbf{t}}) \nonumber\\&\sim \Bigl( \frac{2^{d-1}}{\kappa_{d-2}} \Bigr)^p\, \alpha^p n^p e^{-\zeta (d-1)p R_n/2} e^{\zeta (d-1) d_0^{\prime} t_0/2}{\textbf{1}} \{ t_0\leq \gamma R_n \}\prod_{i=1}^pa_n^{(\gamma)} (d_i^{\prime}) \notag \\&= O \bigl( \rho_n^p e^{\zeta (d-1) d_0^{\prime} \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \bigr). \end{align}
Now, let us take the maximum of
![]() $A_{n,p,\sigma}$
over all
$A_{n,p,\sigma}$
over all
![]() $p\in \{ k-1, \dots, 5(k-1) \}$
,
$p\in \{ k-1, \dots, 5(k-1) \}$
,
![]() $\sigma \in \Sigma_{5(k-1), p}^*$
, and the corresponding spanning tree
$\sigma \in \Sigma_{5(k-1), p}^*$
, and the corresponding spanning tree
![]() $G_{\sigma}^\prime$
of a degree sequence
$G_{\sigma}^\prime$
of a degree sequence
![]() $d_0^{\prime}, d_1^{\prime}, \dots, d_p^{\prime}$
. Equivalently, we take the maximum of
$d_0^{\prime}, d_1^{\prime}, \dots, d_p^{\prime}$
. Equivalently, we take the maximum of
![]() $A_{n,p,\sigma}$
over all
$A_{n,p,\sigma}$
over all
![]() $p\in \{ k-1,\dots, 5(k-1) \}$
and
$p\in \{ k-1,\dots, 5(k-1) \}$
and
![]() $T\in \mathcal G_p^{(1)}$
, to conclude that
$T\in \mathcal G_p^{(1)}$
, to conclude that
 \begin{equation} c_{1,n} = O \Bigg( \max_{\substack{p=k-1,\dots,5(k-1), \\T \in \mathcal{G}_p^{(1)}}} \rho_n^p e^{\zeta (d-1) d_0^{\prime} \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \Bigg).\end{equation}
\begin{equation} c_{1,n} = O \Bigg( \max_{\substack{p=k-1,\dots,5(k-1), \\T \in \mathcal{G}_p^{(1)}}} \rho_n^p e^{\zeta (d-1) d_0^{\prime} \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \Bigg).\end{equation}
If
![]() $\rho_n \to \infty$
, then clearly
$\rho_n \to \infty$
, then clearly
![]() $\rho_n^p = O(\rho_n^{5(k-1)})$
for all
$\rho_n^p = O(\rho_n^{5(k-1)})$
for all
![]() $k-1 \leq p \leq 5(k-1)$
, and hence the bound (45) holds trivially. Otherwise,
$k-1 \leq p \leq 5(k-1)$
, and hence the bound (45) holds trivially. Otherwise,
![]() $\rho_n \to c \in (0,\infty)$
, but we can still easily get (45).
$\rho_n \to c \in (0,\infty)$
, but we can still easily get (45).
Now we shall derive the bound for
![]() $c_{2,n}$
in (46). For
$c_{2,n}$
in (46). For
![]() $p \in \{ k-2,\dots,5(k-2) \}$
, let
$p \in \{ k-2,\dots,5(k-2) \}$
, let
 \begin{align*}\Sigma_{5(k-2),p}^* &= \bigl\{\sigma \in \Sigma_{5(k-2), p}: \sigma((i-1)(k-2)+1),\ldots,\sigma(i(k-2)) \text{ are distinct for all } \nonumber\\[3pt] &\qquad i=1,\dots,5 \bigr\}.\end{align*}
\begin{align*}\Sigma_{5(k-2),p}^* &= \bigl\{\sigma \in \Sigma_{5(k-2), p}: \sigma((i-1)(k-2)+1),\ldots,\sigma(i(k-2)) \text{ are distinct for all } \nonumber\\[3pt] &\qquad i=1,\dots,5 \bigr\}.\end{align*}
Then, arguing as in the derivation of the bounds for
![]() $c_{1,n}$
, we find that the task of bounding
$c_{1,n}$
, we find that the task of bounding
![]() $\mathbb{E}\bigl[ \bigl|D_{x,y}S_n^{(\gamma)}\bigr|^5\bigr]$
is again reduced to that of bounding
$\mathbb{E}\bigl[ \bigl|D_{x,y}S_n^{(\gamma)}\bigr|^5\bigr]$
is again reduced to that of bounding
 \begin{align*}B_{n,p,\sigma} \,{:\!=}\, \mathbb{E}\Bigg[ \sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}} \prod_{i=1}^5g\bigl( x,y, X_{\sigma((i-1)(k-2)+1)},\dots, X_{\sigma(i(k-2))} \bigr) \Bigg]\end{align*}
\begin{align*}B_{n,p,\sigma} \,{:\!=}\, \mathbb{E}\Bigg[ \sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}} \prod_{i=1}^5g\bigl( x,y, X_{\sigma((i-1)(k-2)+1)},\dots, X_{\sigma(i(k-2))} \bigr) \Bigg]\end{align*}
for all
![]() $p \in \{k-2,\ldots,5(k-2)\}$
and
$p \in \{k-2,\ldots,5(k-2)\}$
and
![]() $\sigma \in \Sigma_{5(k-2),p}^*$
.
$\sigma \in \Sigma_{5(k-2),p}^*$
.
Setting
![]() $X_{-1} = x, X_0 = y$
respectively, we can define a simple graph
$X_{-1} = x, X_0 = y$
respectively, we can define a simple graph
![]() $G_\sigma$
on
$G_\sigma$
on
![]() $\{ -1,0 \} \cup [p]$
as in (48) such that
$\{ -1,0 \} \cup [p]$
as in (48) such that
 \begin{align*}\prod_{i=1}^5g\bigl( x,y, X_{\sigma((i-1)(k-2)+1)},\dots, X_{\sigma(i(k-2))} \bigr) = \prod_{(i,j) \in G_{\sigma}}{\textbf{1}} \bigl\{d_\zeta(X_i,X_j) \leq R_n\bigr\}.\end{align*}
\begin{align*}\prod_{i=1}^5g\bigl( x,y, X_{\sigma((i-1)(k-2)+1)},\dots, X_{\sigma(i(k-2))} \bigr) = \prod_{(i,j) \in G_{\sigma}}{\textbf{1}} \bigl\{d_\zeta(X_i,X_j) \leq R_n\bigr\}.\end{align*}
Let
![]() $G_\sigma^{\prime}$
be a spanning tree of
$G_\sigma^{\prime}$
be a spanning tree of
![]() $G_\sigma$
, which exists as
$G_\sigma$
, which exists as
![]() $G_\sigma$
is connected by the surjectivity of
$G_\sigma$
is connected by the surjectivity of
![]() $\sigma$
. Let
$\sigma$
. Let
![]() $d^\prime_{-1},d^\prime_0,\ldots,d^\prime_{p}$
be the respective degrees of vertices
$d^\prime_{-1},d^\prime_0,\ldots,d^\prime_{p}$
be the respective degrees of vertices
![]() $\{-1,0\} \cup [p]$
in
$\{-1,0\} \cup [p]$
in
![]() $G^{\prime}_{\sigma}$
, and let
$G^{\prime}_{\sigma}$
, and let
![]() $E^{\prime}_\sigma$
be its edge set. Note that
$E^{\prime}_\sigma$
be its edge set. Note that
![]() $|E^{\prime}_\sigma|=p+1$
.
$|E^{\prime}_\sigma|=p+1$
.
Then, setting
![]() $t_{-1} = R_n-d_\zeta(0,x)$
and
$t_{-1} = R_n-d_\zeta(0,x)$
and
![]() $t_0=R_n-d_\zeta(0,y)$
(which are deterministic), we again derive that
$t_0=R_n-d_\zeta(0,y)$
(which are deterministic), we again derive that
 \begin{align}B_{n,p,\sigma} &\leq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma}^{\prime},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr]\nonumber\\[3pt]&= n^p \mathbb{P} \bigl(\, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E^{\prime}_\sigma, \ T_i \leq \gamma R_n, \, i=1,\dots,p, \, t_{-1}, t_0 \leq \gamma R_n \bigr). \end{align}
\begin{align}B_{n,p,\sigma} &\leq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma}^{\prime},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr]\nonumber\\[3pt]&= n^p \mathbb{P} \bigl(\, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E^{\prime}_\sigma, \ T_i \leq \gamma R_n, \, i=1,\dots,p, \, t_{-1}, t_0 \leq \gamma R_n \bigr). \end{align}
We basically proceed again as in the derivation of (34) by conditioning on the
![]() $T_i$
, but here, we need to account for one extra complication, i.e., whether
$T_i$
, but here, we need to account for one extra complication, i.e., whether
![]() $(\!-1,0) \in E^{\prime}_{\sigma}$
or not. If
$(\!-1,0) \in E^{\prime}_{\sigma}$
or not. If
![]() $(\!-1,0) \in E^{\prime}_\sigma$
, then whether
$(\!-1,0) \in E^{\prime}_\sigma$
, then whether
![]() $X_{-1}=x$
and
$X_{-1}=x$
and
![]() $X_0=y$
are connected is purely deterministic and the randomness arises only in the remaining p edges. In that case, the rightmost term in (52) is bounded by
$X_0=y$
are connected is purely deterministic and the randomness arises only in the remaining p edges. In that case, the rightmost term in (52) is bounded by
 \begin{align}&n^p \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_p\, {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \} \prod_{(i,j)\in E^{\prime}_\sigma\setminus \{(\!-1,0) \}} \mathbb{P} \bigl( d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}} \bigr)\bar \rho_{n,\alpha} ({\textbf{t}})\nonumber\\[3pt]&\sim C^* n^p e^{-\zeta (d-1)p R_n/2+2^{-1} \zeta (d-1) [ (d_{-1}^{\prime} -1)t_{-1} + (d_0^{\prime} - 1)t_0 ]} {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \}\prod_{i=1}^pa_n^{(\gamma)} (d_i^{\prime}) \notag \\&= O \Bigg( \, \rho_n^p e^{\zeta (d-1) (d_{-1}^{\prime}+d_0^{\prime}) \gamma R_n/2-\zeta(d-1)\gamma R_n} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \, \Bigg). \end{align}
\begin{align}&n^p \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_p\, {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \} \prod_{(i,j)\in E^{\prime}_\sigma\setminus \{(\!-1,0) \}} \mathbb{P} \bigl( d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}} \bigr)\bar \rho_{n,\alpha} ({\textbf{t}})\nonumber\\[3pt]&\sim C^* n^p e^{-\zeta (d-1)p R_n/2+2^{-1} \zeta (d-1) [ (d_{-1}^{\prime} -1)t_{-1} + (d_0^{\prime} - 1)t_0 ]} {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \}\prod_{i=1}^pa_n^{(\gamma)} (d_i^{\prime}) \notag \\&= O \Bigg( \, \rho_n^p e^{\zeta (d-1) (d_{-1}^{\prime}+d_0^{\prime}) \gamma R_n/2-\zeta(d-1)\gamma R_n} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \, \Bigg). \end{align}
On the other hand, if
![]() $(\!-1,0)\notin E^{\prime}_\sigma$
, the randomness arises in all
$(\!-1,0)\notin E^{\prime}_\sigma$
, the randomness arises in all
![]() $p+1$
edges of
$p+1$
edges of
![]() $E^{\prime}_\sigma$
. Then the rightmost term in (52) is bounded by
$E^{\prime}_\sigma$
. Then the rightmost term in (52) is bounded by
 \begin{align}&n^p \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_p\, {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \} \prod_{(i,j)\in E^{\prime}_\sigma} \mathbb{P} \bigl( d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}} \bigr)\bar \rho_{n,\alpha} ({\textbf{t}})\nonumber\\[3pt] &\sim C^* n^p e^{-\zeta (d-1)(p+1) R_n/2 + 2^{-1} \zeta (d-1) (d_{-1}^{\prime}t_{-1}+d_0^{\prime} t_0 )} {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \}\prod_{i=1}^pa_n^{(\gamma)} (d_i^{\prime}) \notag \\&= O \Bigg( \, \rho_n^p e^{-\zeta(d-1)R_n/2+\zeta (d-1) (d_{-1}^{\prime}+d_0^{\prime}) \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \, \Bigg).\end{align}
\begin{align}&n^p \int_0^{\gamma R_n} dt_1 \cdots \int_0^{\gamma R_n} dt_p\, {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \} \prod_{(i,j)\in E^{\prime}_\sigma} \mathbb{P} \bigl( d_\zeta(X_i,X_j)\leq R_n\, |\, {\textbf{t}} \bigr)\bar \rho_{n,\alpha} ({\textbf{t}})\nonumber\\[3pt] &\sim C^* n^p e^{-\zeta (d-1)(p+1) R_n/2 + 2^{-1} \zeta (d-1) (d_{-1}^{\prime}t_{-1}+d_0^{\prime} t_0 )} {\textbf{1}} \{ t_{-1}, t_0\leq \gamma R_n \}\prod_{i=1}^pa_n^{(\gamma)} (d_i^{\prime}) \notag \\&= O \Bigg( \, \rho_n^p e^{-\zeta(d-1)R_n/2+\zeta (d-1) (d_{-1}^{\prime}+d_0^{\prime}) \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \, \Bigg).\end{align}
Combining (53) and (54), we conclude that
 \begin{align*}B_{n,p,\sigma} = O \bigl( \, \rho_n^p e^{\zeta (d-1) (d_{-1}^{\prime}+d_0^{\prime}) \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \, \bigr).\end{align*}
\begin{align*}B_{n,p,\sigma} = O \bigl( \, \rho_n^p e^{\zeta (d-1) (d_{-1}^{\prime}+d_0^{\prime}) \gamma R_n/2} \prod_{i=1}^pa_n^{(\gamma)}(d^{\prime}_i) \, \bigr).\end{align*}
Now, proceeding as in the derivation of (45) (see below (51)), we get (46).
Proof of Lemma 6. From the same reasoning as in Lemma 5, it suffices to bound
 \begin{equation*}C_{n,p,\sigma} \,{:\!=}\! \int_0^{\gamma R_n}\!\!\int_{C_d}\mathbb{E} \Bigg[ \sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}} \prod_{i=1}^3g\bigl(x,X_{\sigma((i-1)(k-1)+1)},\ldots, X_{\sigma(i(k-1))}\bigr) \!\Bigg] \bar \rho_{n,\alpha}(t) \pi(\theta) \mathrm{d} \theta \mathrm{d} t\end{equation*}
\begin{equation*}C_{n,p,\sigma} \,{:\!=}\! \int_0^{\gamma R_n}\!\!\int_{C_d}\mathbb{E} \Bigg[ \sum_{(X_1,\ldots, X_p) \in \mathcal{P}^{p}_{n,\neq}} \prod_{i=1}^3g\bigl(x,X_{\sigma((i-1)(k-1)+1)},\ldots, X_{\sigma(i(k-1))}\bigr) \!\Bigg] \bar \rho_{n,\alpha}(t) \pi(\theta) \mathrm{d} \theta \mathrm{d} t\end{equation*}
for every
![]() $p \in \{ k-1,\dots,3(k-1) \}$
and
$p \in \{ k-1,\dots,3(k-1) \}$
and
![]() $\sigma \in \Sigma_{3(k-1),p}^*$
.
$\sigma \in \Sigma_{3(k-1),p}^*$
.
Let
![]() $G_\sigma$
be the same simple graph on
$G_\sigma$
be the same simple graph on
![]() $\{0\} \cup [p]$
as that constructed in the proof of Lemma 5(i) (see (48)), for which x is identified as a vertex ‘0’. Once again, let
$\{0\} \cup [p]$
as that constructed in the proof of Lemma 5(i) (see (48)), for which x is identified as a vertex ‘0’. Once again, let
![]() $G^{\prime}_{\sigma}$
be a spanning tree of
$G^{\prime}_{\sigma}$
be a spanning tree of
![]() $G_{\sigma}$
, with
$G_{\sigma}$
, with
![]() $d_0^{\prime},\dots, d_p^{\prime}$
the degree sequence and
$d_0^{\prime},\dots, d_p^{\prime}$
the degree sequence and
![]() $E^{\prime}_\sigma$
the edge set of
$E^{\prime}_\sigma$
the edge set of
![]() $G_\sigma^{\prime}$
. It follows from the monotonicity of
$G_\sigma^{\prime}$
. It follows from the monotonicity of
![]() ${\mathcal{C}}$
and the Mecke formula that
${\mathcal{C}}$
and the Mecke formula that
 \begin{align}C_{n,p,\sigma} &\leq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma}^{\prime},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr] \nonumber\\[3pt] &= n^p \mathbb{P} \bigl(\, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E^{\prime}_\sigma, \ T_i \leq \gamma R_n, \, i=0,\dots,p \, \bigr). \end{align}
\begin{align}C_{n,p,\sigma} &\leq \mathbb{E}\Bigl[\, {\mathcal{C}}\bigl(G_{\sigma}^{\prime},HG^{(\gamma)}_n(R_n;\ \alpha,\zeta)\bigr)\Bigr] \nonumber\\[3pt] &= n^p \mathbb{P} \bigl(\, d_\zeta(X_i,X_j) \leq R_n, \ (i,j)\in E^{\prime}_\sigma, \ T_i \leq \gamma R_n, \, i=0,\dots,p \, \bigr). \end{align}
For further calculations, we note that
![]() $X_0$
in (55) is random, whereas
$X_0$
in (55) is random, whereas
![]() $X_0=x$
in (49) was purely deterministic. Taking into consideration this difference and using Theorem 1 with
$X_0=x$
in (49) was purely deterministic. Taking into consideration this difference and using Theorem 1 with
![]() $k=p+1$
, we have
$k=p+1$
, we have
 \begin{align*}C_{n,p,\sigma} \leq C^* \rho_n^p \prod_{i=0}^p a_n^{(\gamma)} (d_i^\prime) = O \Bigl( \rho_n^{3(k-1)} \prod_{i=0}^p a_n^{(\gamma)} (d_i^\prime)\Bigr).\end{align*}
\begin{align*}C_{n,p,\sigma} \leq C^* \rho_n^p \prod_{i=0}^p a_n^{(\gamma)} (d_i^\prime) = O \Bigl( \rho_n^{3(k-1)} \prod_{i=0}^p a_n^{(\gamma)} (d_i^\prime)\Bigr).\end{align*}
Finally, taking the maximum completes the proof.
Proof of Lemma 7. We first need the following fact. For
![]() $0 < \gamma <1/2$
, let
$0 < \gamma <1/2$
, let
![]() $HG({\mathcal{X}})$
be a hyperbolic geometric graph on a point set
$HG({\mathcal{X}})$
be a hyperbolic geometric graph on a point set
![]() ${\mathcal{X}} \subset D_{\gamma}(R_n)$
, connecting any two points within a distance
${\mathcal{X}} \subset D_{\gamma}(R_n)$
, connecting any two points within a distance
![]() $R_n$
. Suppose that
$R_n$
. Suppose that
![]() $y_1,y_2 \in {\mathcal{X}}$
are connected by a path of length
$y_1,y_2 \in {\mathcal{X}}$
are connected by a path of length
![]() $\ell \geq 1$
in
$\ell \geq 1$
in
![]() $HG({\mathcal{X}})$
, and their hyperbolic distances from the boundary, given by
$HG({\mathcal{X}})$
, and their hyperbolic distances from the boundary, given by
![]() $t_i = R_n-d_\zeta(0,y_i)$
,
$t_i = R_n-d_\zeta(0,y_i)$
,
![]() $i=1,2$
, satisfy
$i=1,2$
, satisfy
![]() $t_1,t_2 \leq \gamma R_n$
. For the relative angle
$t_1,t_2 \leq \gamma R_n$
. For the relative angle
![]() $\theta_{12}$
between
$\theta_{12}$
between
![]() $y_1$
and
$y_1$
and
![]() $y_2$
, we claim that
$y_2$
, we claim that
uniformly for
![]() $t_1,t_2 \leq \gamma R_n$
.
$t_1,t_2 \leq \gamma R_n$
.
The proof of (56) can be done inductively. For
![]() $\ell=1$
, set
$\ell=1$
, set
![]() $\hat \theta_{12} = \bigl( e^{-2\zeta (R_n-t_1)} + e^{-2\zeta (R_n-t_2)} \bigr)^{1/2}$
as in Lemma 3. Since
$\hat \theta_{12} = \bigl( e^{-2\zeta (R_n-t_1)} + e^{-2\zeta (R_n-t_2)} \bigr)^{1/2}$
as in Lemma 3. Since
![]() $t_1 + t_2 \leq 2\gamma R_n < R_n-\omega_n$
, we get
$t_1 + t_2 \leq 2\gamma R_n < R_n-\omega_n$
, we get
as in the proof of Lemma 4.
If
![]() $\theta_{12} \leq \hat \theta_{12}$
, then
$\theta_{12} \leq \hat \theta_{12}$
, then
![]() $\theta_{12} \leq \bigl(1+o(1)\bigr)e^{-\zeta (1-2\gamma) R_n/2}$
by (57) with
$\theta_{12} \leq \bigl(1+o(1)\bigr)e^{-\zeta (1-2\gamma) R_n/2}$
by (57) with
![]() $t_1, t_2 \le \gamma R_n$
, and so (56) holds for
$t_1, t_2 \le \gamma R_n$
, and so (56) holds for
![]() $\ell=1$
. If
$\ell=1$
. If
![]() $\theta_{12}\gg \hat \theta_{12}$
, Lemma 3 yields the following: uniformly for
$\theta_{12}\gg \hat \theta_{12}$
, Lemma 3 yields the following: uniformly for
![]() $t_i \leq \gamma R_n$
,
$t_i \leq \gamma R_n$
,
![]() $i=1,2$
, we have that
$i=1,2$
, we have that
 \begin{align*}R_n &\geq d_\zeta(y_1,y_2) = 2R_n -(t_1+t_2) + \frac{2}{\zeta} \log \sin \Bigl(\frac{\theta_{12}}{2} \Bigr) + o(1) \\[3pt] &\geq 2(1-\gamma) R_n + \frac{2}{\zeta} \log \sin \Bigl(\frac{\theta_{12}}{2} \Bigr) + o(1), \ \ \ n\to\infty.\end{align*}
\begin{align*}R_n &\geq d_\zeta(y_1,y_2) = 2R_n -(t_1+t_2) + \frac{2}{\zeta} \log \sin \Bigl(\frac{\theta_{12}}{2} \Bigr) + o(1) \\[3pt] &\geq 2(1-\gamma) R_n + \frac{2}{\zeta} \log \sin \Bigl(\frac{\theta_{12}}{2} \Bigr) + o(1), \ \ \ n\to\infty.\end{align*}
Equivalently, we get that
![]() $\sin \big(\theta_{12}/2 \big) \le \big( 1+o(1) \big) e^{-\zeta (1-2\gamma) R_n/2}$
. As the right-hand side tends to 0 as
$\sin \big(\theta_{12}/2 \big) \le \big( 1+o(1) \big) e^{-\zeta (1-2\gamma) R_n/2}$
. As the right-hand side tends to 0 as
![]() $n\to\infty$
, we have, uniformly for
$n\to\infty$
, we have, uniformly for
![]() $t_i \leq \gamma R_n$
,
$t_i \leq \gamma R_n$
,
![]() $i=1,2$
,
$i=1,2$
,
Hence, in either case, the claim for
![]() $\ell = 1$
follows.
$\ell = 1$
follows.
Now, suppose that the claim holds for
![]() $\ell-1$
. Then, if
$\ell-1$
. Then, if
![]() $y_1,y_2$
have a path of length
$y_1,y_2$
have a path of length
![]() $\ell$
, there exists a
$\ell$
, there exists a
![]() $y_0$
such that
$y_0$
such that
![]() $y_1$
and
$y_1$
and
![]() $y_0$
have a path of length
$y_0$
have a path of length
![]() $\ell-1$
, and
$\ell-1$
, and
![]() $y_0$
and
$y_0$
and
![]() $y_2$
have a path of length 1. Denoting the corresponding relative angles by
$y_2$
have a path of length 1. Denoting the corresponding relative angles by
![]() $\theta_{10}$
and
$\theta_{10}$
and
![]() $\theta_{02}$
, we see that
$\theta_{02}$
, we see that
![]() $\theta_{12} \leq \theta_{10} + \theta_{02}$
; hence, the proof of (56) can be completed by the induction hypothesis.
$\theta_{12} \leq \theta_{10} + \theta_{02}$
; hence, the proof of (56) can be completed by the induction hypothesis.
Fix
![]() $x_1,x_2,x_3$
such that
$x_1,x_2,x_3$
such that
![]() $t_i \leq \gamma R_n$
for
$t_i \leq \gamma R_n$
for
![]() $i =1,2,3$
. From (43),
$i =1,2,3$
. From (43),
![]() $D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0$
implies that there is a path of length at most
$D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0$
implies that there is a path of length at most
![]() $diam(\Gamma_k)$
(i.e., the diameter of the graph) from
$diam(\Gamma_k)$
(i.e., the diameter of the graph) from
![]() $x_1$
to
$x_1$
to
![]() $x_3$
in the hyperbolic random geometric graph on
$x_3$
in the hyperbolic random geometric graph on
![]() $\bigl( \mathcal{P}_n \cap D_{\gamma}(R_n) \bigr) \cup \{x_1,x_3\}$
with radius of connectivity
$\bigl( \mathcal{P}_n \cap D_{\gamma}(R_n) \bigr) \cup \{x_1,x_3\}$
with radius of connectivity
![]() $R_n$
. Thus, from (56) and
$R_n$
. Thus, from (56) and
![]() $diam(\Gamma_k) \leq k$
, we have that
$diam(\Gamma_k) \leq k$
, we have that
Therefore,
 \begin{align*}&\int_{[0,\gamma R_n]^3 \times C_d^3} \big[ \mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}\big(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0\big) \big]^a \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \\[3pt]&\leq C^* \int_{[0,\gamma R_n]^3 \times C_d^3} {\textbf{1}} \big\{ \theta_{j3} \leq 2ke^{-\zeta (1-2\gamma)R_n/2}, \, j=1,2 \Big\} \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \\[3pt]&= C^* \mathbb{P} \bigl( \Theta_{j3} \leq 2k e^{-\zeta (1-2\gamma)R_n/2}, \, j=1,2, \ T_i \leq \gamma R_n, \ i=1,2,3 \bigr),\end{align*}
\begin{align*}&\int_{[0,\gamma R_n]^3 \times C_d^3} \big[ \mathbb{P}(D^2_{x_1,x_3}S_n^{(\gamma)} \neq 0)\mathbb{P}\big(D^2_{x_2,x_3}S_n^{(\gamma)} \neq 0\big) \big]^a \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \\[3pt]&\leq C^* \int_{[0,\gamma R_n]^3 \times C_d^3} {\textbf{1}} \big\{ \theta_{j3} \leq 2ke^{-\zeta (1-2\gamma)R_n/2}, \, j=1,2 \Big\} \prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\pi(\theta_i) \mathrm{d} t_i \mathrm{d} \theta_i \\[3pt]&= C^* \mathbb{P} \bigl( \Theta_{j3} \leq 2k e^{-\zeta (1-2\gamma)R_n/2}, \, j=1,2, \ T_i \leq \gamma R_n, \ i=1,2,3 \bigr),\end{align*}
where
![]() $\Theta_{j3}$
denotes the relative angle between
$\Theta_{j3}$
denotes the relative angle between
![]() $X_j$
and
$X_j$
and
![]() $X_3$
,
$X_3$
,
![]() $j=1,2$
, and
$j=1,2$
, and
![]() $T_i=R_n-d_\zeta(0,X_i)$
for
$T_i=R_n-d_\zeta(0,X_i)$
for
![]() $i=1,2,3$
.
$i=1,2,3$
.
Now, the probability of the last term equals
 \begin{equation} \int_{[0,\gamma R_n]^3} \prod_{j=1}^2 \mathbb{P} \bigl( \Theta_{j3} \leq 2ke^{-\zeta (1-2\gamma)R_n/2}\, | \, t_1,t_2,t_3 \bigr)\prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\, \mathrm{d} t_i.\end{equation}
\begin{equation} \int_{[0,\gamma R_n]^3} \prod_{j=1}^2 \mathbb{P} \bigl( \Theta_{j3} \leq 2ke^{-\zeta (1-2\gamma)R_n/2}\, | \, t_1,t_2,t_3 \bigr)\prod_{i=1}^3\bar \rho_{n,\alpha}(t_i)\, \mathrm{d} t_i.\end{equation}
Using the density (28) of a relative angle, it is easy to see that
 \begin{align*}\prod_{j=1}^2 \mathbb{P} \bigl( \Theta_{j3} \leq 2ke^{-\zeta (1-2\gamma)R_n/2}\, | \, t_1,t_2,t_3 \bigr) \sim \biggl( \frac{(2k)^{d-1}}{(d-1)\kappa_{d-2}} \biggr)^2 e^{-\zeta (d-1) (1-2\gamma) R_n}, \ \ n\to\infty,\end{align*}
\begin{align*}\prod_{j=1}^2 \mathbb{P} \bigl( \Theta_{j3} \leq 2ke^{-\zeta (1-2\gamma)R_n/2}\, | \, t_1,t_2,t_3 \bigr) \sim \biggl( \frac{(2k)^{d-1}}{(d-1)\kappa_{d-2}} \biggr)^2 e^{-\zeta (d-1) (1-2\gamma) R_n}, \ \ n\to\infty,\end{align*}
uniformly for
![]() $t_i \leq \gamma R_n$
,
$t_i \leq \gamma R_n$
,
![]() $i=1,2,3$
. It now follows from Lemma 1(ii) that (58) is asymptotically equal to
$i=1,2,3$
. It now follows from Lemma 1(ii) that (58) is asymptotically equal to
This proves the first statement in the lemma. By exactly the same argument, we obtain the second statement in the lemma.
3.3.3. Proof of the central limit theorem in Theorem 3
We now put together all the bounds and prove our main CLT.
Proof of Theorem 3. From (16), we have
 \begin{align*}\mathbb{V}ar(S_n^{(\gamma)}) = \Omega \biggl( n \rho_n^{2(k-1)}a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2 \biggr).\end{align*}
\begin{align*}\mathbb{V}ar(S_n^{(\gamma)}) = \Omega \biggl( n \rho_n^{2(k-1)}a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2 \biggr).\end{align*}
Substituting the lower bound for variance above and the bounds in Lemmas 5–7 into (44), and using the definition of
![]() $\rho_n$
, we obtain
$\rho_n$
, we obtain
 \begin{align*}W_1 &\leq C^* n^{-1/2} \frac{(c^{\prime}_{1, n}c^{\prime}_{2, n})^{1/5}e^{\gamma \zeta (d-1) R_n}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} , \\[5pt]W_2 &\leq C^* n^{-1/2} \rho_n^{-1} \frac{(c^{\prime}_{2, n})^{2/5}e^{\gamma \zeta (d-1) R_n}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} , \\[5pt]W_3 &\leq C^* n^{-1/2} \frac{c^{\prime}_{3,n}}{a_n^{(\gamma)}(2d_{(k)})^{3/2} \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^3}.\end{align*}
\begin{align*}W_1 &\leq C^* n^{-1/2} \frac{(c^{\prime}_{1, n}c^{\prime}_{2, n})^{1/5}e^{\gamma \zeta (d-1) R_n}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} , \\[5pt]W_2 &\leq C^* n^{-1/2} \rho_n^{-1} \frac{(c^{\prime}_{2, n})^{2/5}e^{\gamma \zeta (d-1) R_n}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} , \\[5pt]W_3 &\leq C^* n^{-1/2} \frac{c^{\prime}_{3,n}}{a_n^{(\gamma)}(2d_{(k)})^{3/2} \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^3}.\end{align*}
From Theorem 4, we know that
 \begin{equation*}d_W\left(\frac{S_n^{(\gamma)} - \mathbb{E}\left(S_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) \leq W_1 + W_2 + W_3.\end{equation*}
\begin{equation*}d_W\left(\frac{S_n^{(\gamma)} - \mathbb{E}\left(S_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) \leq W_1 + W_2 + W_3.\end{equation*}
By the definition of
![]() $a_n^{(\gamma)}$
, one can see that
$a_n^{(\gamma)}$
, one can see that
 \begin{align*}c_{1,n}^{\prime} &\le C^* \max_{\substack{p=k-1,\dots,5(k-1), \\ T\in \mathcal G_p^{(1)}}} e^{2^{-1}\zeta(d-1) \big[ d_0^{\prime} +\sum_{i=1}^p \big( d_i^{\prime}-2\alpha/\zeta \big)_+ \big]\gamma R_n}, \\c_{2,n}^{\prime} &\le C^* \max_{\substack{p=k-2,\dots,5(k-2), \\ T\in \mathcal G_p^{(2)}}} e^{2^{-1}\zeta(d-1) \big[ d_{-1}^{\prime}+ d_0^{\prime} +\sum_{i=1}^p \big( d_i^{\prime}-2\alpha/\zeta \big)_+ \big]\gamma R_n}, \\c_{3,n}^{\prime} &\le C^* \max_{\substack{p=k-1,\dots,3(k-1), \\ T\in \mathcal G_p^{(1)}}} e^{2^{-1}\zeta(d-1) \sum_{i=0}^p \big( d_i^{\prime}-2\alpha/\zeta \big)_+ \gamma R_n}, \\a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2 &\ge C^* e^{2^{-1}\zeta(d-1) \big[ 2\big( d_{(k)}-\alpha/\zeta \big)_+ +\sum_{i=1}^{k-1} \big( d_{(i)}-2\alpha/\zeta \big)_+ \big]\gamma R_n}.\end{align*}
\begin{align*}c_{1,n}^{\prime} &\le C^* \max_{\substack{p=k-1,\dots,5(k-1), \\ T\in \mathcal G_p^{(1)}}} e^{2^{-1}\zeta(d-1) \big[ d_0^{\prime} +\sum_{i=1}^p \big( d_i^{\prime}-2\alpha/\zeta \big)_+ \big]\gamma R_n}, \\c_{2,n}^{\prime} &\le C^* \max_{\substack{p=k-2,\dots,5(k-2), \\ T\in \mathcal G_p^{(2)}}} e^{2^{-1}\zeta(d-1) \big[ d_{-1}^{\prime}+ d_0^{\prime} +\sum_{i=1}^p \big( d_i^{\prime}-2\alpha/\zeta \big)_+ \big]\gamma R_n}, \\c_{3,n}^{\prime} &\le C^* \max_{\substack{p=k-1,\dots,3(k-1), \\ T\in \mathcal G_p^{(1)}}} e^{2^{-1}\zeta(d-1) \sum_{i=0}^p \big( d_i^{\prime}-2\alpha/\zeta \big)_+ \gamma R_n}, \\a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2 &\ge C^* e^{2^{-1}\zeta(d-1) \big[ 2\big( d_{(k)}-\alpha/\zeta \big)_+ +\sum_{i=1}^{k-1} \big( d_{(i)}-2\alpha/\zeta \big)_+ \big]\gamma R_n}.\end{align*}
Note also that (18) ensures
![]() $R_n\le C^* \log n$
. Substituting all of these bounds back into
$R_n\le C^* \log n$
. Substituting all of these bounds back into
![]() $W_1, W_2$
, and
$W_1, W_2$
, and
![]() $W_3$
above, we find that
$W_3$
above, we find that
for some positive constants
![]() $c_i$
,
$c_i$
,
![]() $i=1,2,3$
. Hence, for any
$i=1,2,3$
. Hence, for any
![]() $a < 1/2$
, we can choose
$a < 1/2$
, we can choose
![]() $\gamma_0$
so small that
$\gamma_0$
so small that
![]() $W_1 + W_2 + W_3 = O(n^{-a})$
as
$W_1 + W_2 + W_3 = O(n^{-a})$
as
![]() $n \to \infty$
, for all
$n \to \infty$
, for all
![]() $0 < \gamma < \gamma_0$
. This proves the Wasserstein bound in (19).
$0 < \gamma < \gamma_0$
. This proves the Wasserstein bound in (19).
To prove the Kolmogorov bound in (19), again using the bounds in Theorem 4, along with Lemmas 5, 6, and 7 and the variance lower bound above, we derive using (44) that
 \begin{align*}W_4 &\leq C^* n^{-1/2} \biggl[ \, \frac{(c^{\prime}_{1,n})^{3/5}}{a_n^{(\gamma)}(2d_{(k)})^{3/2} \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^3} + \frac{(c^{\prime}_{1,n})^{4/5}}{a_n^{(\gamma)}(2d_{(k)})^2 \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^4} \, \biggr] , \\[5pt]W_5 &\leq C^* n^{-1/2} \frac{(c^{\prime}_{1,n})^{2/5}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} , \\[5pt]W_6 &\leq C^* (n\rho_n)^{-1/2} \frac{e^{\gamma \zeta (d-1) R_n/2}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} \bigl((c^{\prime}_{1,n}c^{\prime}_{2,n})^{1/5} + \rho_n^{-1} (c^{\prime}_{2,n})^{2/5}\bigr).\end{align*}
\begin{align*}W_4 &\leq C^* n^{-1/2} \biggl[ \, \frac{(c^{\prime}_{1,n})^{3/5}}{a_n^{(\gamma)}(2d_{(k)})^{3/2} \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^3} + \frac{(c^{\prime}_{1,n})^{4/5}}{a_n^{(\gamma)}(2d_{(k)})^2 \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^4} \, \biggr] , \\[5pt]W_5 &\leq C^* n^{-1/2} \frac{(c^{\prime}_{1,n})^{2/5}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} , \\[5pt]W_6 &\leq C^* (n\rho_n)^{-1/2} \frac{e^{\gamma \zeta (d-1) R_n/2}}{a_n^{(\gamma)}(2d_{(k)}) \prod_{i=1}^{k-1} a_n^{(\gamma)}(d_{(i)})^2} \bigl((c^{\prime}_{1,n}c^{\prime}_{2,n})^{1/5} + \rho_n^{-1} (c^{\prime}_{2,n})^{2/5}\bigr).\end{align*}
From Theorem 4, we have
 \begin{equation*}d_K\left(\frac{S_n^{(\gamma)} - \mathbb{E}(S_n^{(\gamma)})}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) \leq W_1 + W_2 + W_3 + W_4 + W_5 + W_6.\end{equation*}
\begin{equation*}d_K\left(\frac{S_n^{(\gamma)} - \mathbb{E}(S_n^{(\gamma)})}{\sqrt{\mathbb{V}ar(S_n^{(\gamma)})}},N\right) \leq W_1 + W_2 + W_3 + W_4 + W_5 + W_6.\end{equation*}
Substituting the bounds for
![]() $c_{1,n}^{\prime}$
,
$c_{1,n}^{\prime}$
,
![]() $c_{2,n}^{\prime}$
, and
$c_{2,n}^{\prime}$
, and
![]() $c_{3,n}^{\prime}$
into
$c_{3,n}^{\prime}$
into
![]() $W_4, W_5$
, and
$W_4, W_5$
, and
![]() $W_6$
, as well as
$W_6$
, as well as
![]() $R_n\le C^* \log n$
, one can see that
$R_n\le C^* \log n$
, one can see that
for some
![]() $c_i>0$
,
$c_i>0$
,
![]() $i=4,5,6$
. Now, for any
$i=4,5,6$
. Now, for any
![]() $a < 1/2$
, we can choose
$a < 1/2$
, we can choose
![]() $\gamma_0$
small enough so that the Kolmogorov bound in (19) holds for all
$\gamma_0$
small enough so that the Kolmogorov bound in (19) holds for all
![]() $0< \gamma < \gamma_0$
.
$0< \gamma < \gamma_0$
.
In order to show (20), let us assume
![]() $\alpha / \zeta > d_{(k)}$
. First, choose
$\alpha / \zeta > d_{(k)}$
. First, choose
![]() $0<\gamma<1/2$
such that
$0<\gamma<1/2$
such that
 \begin{align*}d_W\left(\frac{S_n^{(\gamma)} - \mathbb{E}\left(S_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar\left(S_n^{(\gamma)}\right)}},N\right) \to 0, \ \ \text{as } n\to\infty.\end{align*}
\begin{align*}d_W\left(\frac{S_n^{(\gamma)} - \mathbb{E}\left(S_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar\left(S_n^{(\gamma)}\right)}},N\right) \to 0, \ \ \text{as } n\to\infty.\end{align*}
Setting
![]() $U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
, we write
$U_n^{(\gamma)} = S_n - S_n^{(\gamma)}$
, we write
 \begin{align*} \frac{S_n - \mathbb{E}(S_n)}{\sqrt{\mathbb{V}ar(S_n)}} = \sqrt{\frac{\mathbb{V}ar\left(S_n^{(\gamma)}\right)}{\mathbb{V}ar(S_n)}} \times \frac{S_n^{(\gamma)} - \mathbb{E}\left(S_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar\left(S_n^{(\gamma)}\right)}} + \frac{U_n^{(\gamma)} - \mathbb{E}\left(U_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar(S_n)}}. \end{align*}
\begin{align*} \frac{S_n - \mathbb{E}(S_n)}{\sqrt{\mathbb{V}ar(S_n)}} = \sqrt{\frac{\mathbb{V}ar\left(S_n^{(\gamma)}\right)}{\mathbb{V}ar(S_n)}} \times \frac{S_n^{(\gamma)} - \mathbb{E}\left(S_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar\left(S_n^{(\gamma)}\right)}} + \frac{U_n^{(\gamma)} - \mathbb{E}\left(U_n^{(\gamma)}\right)}{\sqrt{\mathbb{V}ar(S_n)}}. \end{align*}
From (17), we have that
![]() $\mathbb{V}ar\left(S_n^{(\gamma)}\right) \sim \mathbb{V}ar(S_n)$
as
$\mathbb{V}ar\left(S_n^{(\gamma)}\right) \sim \mathbb{V}ar(S_n)$
as
![]() $n \to \infty$
. Since the CLT holds for
$n \to \infty$
. Since the CLT holds for
![]() $S_n^{(\gamma)}$
, the first term converges in distribution to N as
$S_n^{(\gamma)}$
, the first term converges in distribution to N as
![]() $n \to \infty.$
Now, from (41), we know that
$n \to \infty.$
Now, from (41), we know that
![]() $\mathbb{V}ar\left(U_n^{(\gamma)}\right) / \mathbb{V}ar(S_n) \to 0$
as
$\mathbb{V}ar\left(U_n^{(\gamma)}\right) / \mathbb{V}ar(S_n) \to 0$
as
![]() $n \to \infty$
, and hence, by Chebyshev’s inequality, the second term converges to 0 in probability. Thus, applying Slutsky’s theorem, we obtain the CLT for
$n \to \infty$
, and hence, by Chebyshev’s inequality, the second term converges to 0 in probability. Thus, applying Slutsky’s theorem, we obtain the CLT for
![]() $S_n$
as required.
$S_n$
as required.
Remark 4. If
![]() $2\alpha / \zeta > 5d_{(k)}$
, one can deduce more precise estimates for
$2\alpha / \zeta > 5d_{(k)}$
, one can deduce more precise estimates for
![]() $W_i$
,
$W_i$
,
![]() $i=1,\dots,6$
. In fact, by the choice of the
$i=1,\dots,6$
. In fact, by the choice of the
![]() $d_i$
, we have that each
$d_i$
, we have that each
![]() $a_n^{(\gamma)}(d^{\prime}_i)$
converges to a constant, and so we derive that
$a_n^{(\gamma)}(d^{\prime}_i)$
converges to a constant, and so we derive that
![]() $c^{\prime}_{i,n} \leq C^* (n/\rho_n)^{5(k-1)\gamma}$
for
$c^{\prime}_{i,n} \leq C^* (n/\rho_n)^{5(k-1)\gamma}$
for
![]() $i = 1,2$
. Thus we have that
$i = 1,2$
. Thus we have that
 \begin{align*} W_1 \leq C^* n^{-1/2 + 2k\gamma} \rho_n^{-2k\gamma}, \qquad W_2 \leq C^* n^{-1/2 + 2k\gamma} \rho_n^{-1-2k\gamma},\\[3pt]W_3 \leq C^*n^{-1/2}, \qquad W_4 \leq C^* n^{-1/2 + 4(k-1)\gamma} \rho_n^{-4(k-1)\gamma},\\[3pt]W_5 \leq C^* n^{-1/2 + 2(k-1)\gamma} \rho_n^{-2(k-1)\gamma}, \qquad W_6 \leq C^* n^{-1/2 + (2k-1)\gamma} \rho_n^{-1/2 - (2k-1)\gamma}.\end{align*}
\begin{align*} W_1 \leq C^* n^{-1/2 + 2k\gamma} \rho_n^{-2k\gamma}, \qquad W_2 \leq C^* n^{-1/2 + 2k\gamma} \rho_n^{-1-2k\gamma},\\[3pt]W_3 \leq C^*n^{-1/2}, \qquad W_4 \leq C^* n^{-1/2 + 4(k-1)\gamma} \rho_n^{-4(k-1)\gamma},\\[3pt]W_5 \leq C^* n^{-1/2 + 2(k-1)\gamma} \rho_n^{-2(k-1)\gamma}, \qquad W_6 \leq C^* n^{-1/2 + (2k-1)\gamma} \rho_n^{-1/2 - (2k-1)\gamma}.\end{align*}
In particular, the above inequalities imply that
![]() $W_i \to 0$
for
$W_i \to 0$
for
![]() $i = 1,\ldots,6$
, whenever
$i = 1,\ldots,6$
, whenever
![]() $\gamma < 1/8(k-1)$
.
$\gamma < 1/8(k-1)$
.
Appendix A
In this appendix, we state the main normal approximation result in [Reference Last, Peccati and Schulte32] and explain how Theorem 4 can be deduced from the same. Recall the notation from Section 3.3.1.
Theorem 5. ([Reference Last, Peccati and Schulte32, Theorems 1.1 and 1.2]) Let F be as in Theorem 4. Then
 \begin{eqnarray*}d_W\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & \gamma_1(F) + \gamma_2(F) + \gamma_3(F), \\[3pt]d_K\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & \gamma_1(F) + \gamma_2(F) + \gamma_3(F) + \gamma_4(F) + \gamma_5(F) + \gamma_6(F),\end{eqnarray*}
\begin{eqnarray*}d_W\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & \gamma_1(F) + \gamma_2(F) + \gamma_3(F), \\[3pt]d_K\left(\frac{F-\mathbb{E}(F)}{\sqrt{\mathbb{V}ar(F)}},N\right) & \leq & \gamma_1(F) + \gamma_2(F) + \gamma_3(F) + \gamma_4(F) + \gamma_5(F) + \gamma_6(F),\end{eqnarray*}
where
![]() $\gamma_i(F)$
,
$\gamma_i(F)$
,
![]() $i = 1,\ldots,6,$
are given by
$i = 1,\ldots,6,$
are given by
 \begin{align*}\gamma_1(F) &\,{:\!=}\, \frac{2}{\mathbb{V}ar(F)}\left[ \int_{{\textbf{X}}^3} \Big( \mathbb{E}([D_{x_1}F]^2[D_{x_2}F]^2) \mathbb{E}([D^2_{x_1,x_3}F]^2[D^2_{x_2,x_3}F]^2) \Big)^{1/2} \lambda^3(\mathrm{d}(x_1,x_2,x_3)) \right]^{1/2}, \\[3pt]\gamma_2(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^3} \mathbb{E}([D^2_{x_1,x_3}F]^2[D^2_{x_2,x_3}F]^2) \lambda^3(\mathrm{d} (x_1,x_2,x_3)) \right]^{1/2}, \\[3pt]\gamma_3(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)^{3/2}} \int_{{\textbf{X}}} \mathbb{E}(|D_xF|^3) \lambda(\mathrm{d} x), \\[3pt]\gamma_4(F) &\,{:\!=}\, \frac{1}{2\mathbb{V}ar(F)^2} \left[ \mathbb{E}([F - \mathbb{E}(F)]^4)\right]^{1/4} \int_{{\textbf{X}}} \big[\mathbb{E}([D_xF]^4)\big]^{3/4} \lambda(\mathrm{d} x), \\[3pt]\gamma_5(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}} \mathbb{E}([D_xF]^4) \lambda(\mathrm{d} x) \right]^{1/2}, \\[3pt]\gamma_6(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^2} 6 \Big( \mathbb{E}([D_{x_1}F]^4) \mathbb{E}([D^2_{x_1,x_2}F]^4) \Big)^{1/2} + 3 \mathbb{E}([D^2_{x_1,x_2}F]^4) \lambda^2(\mathrm{d}(x_1,x_2)) \right]^{1/2}.\end{align*}
\begin{align*}\gamma_1(F) &\,{:\!=}\, \frac{2}{\mathbb{V}ar(F)}\left[ \int_{{\textbf{X}}^3} \Big( \mathbb{E}([D_{x_1}F]^2[D_{x_2}F]^2) \mathbb{E}([D^2_{x_1,x_3}F]^2[D^2_{x_2,x_3}F]^2) \Big)^{1/2} \lambda^3(\mathrm{d}(x_1,x_2,x_3)) \right]^{1/2}, \\[3pt]\gamma_2(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^3} \mathbb{E}([D^2_{x_1,x_3}F]^2[D^2_{x_2,x_3}F]^2) \lambda^3(\mathrm{d} (x_1,x_2,x_3)) \right]^{1/2}, \\[3pt]\gamma_3(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)^{3/2}} \int_{{\textbf{X}}} \mathbb{E}(|D_xF|^3) \lambda(\mathrm{d} x), \\[3pt]\gamma_4(F) &\,{:\!=}\, \frac{1}{2\mathbb{V}ar(F)^2} \left[ \mathbb{E}([F - \mathbb{E}(F)]^4)\right]^{1/4} \int_{{\textbf{X}}} \big[\mathbb{E}([D_xF]^4)\big]^{3/4} \lambda(\mathrm{d} x), \\[3pt]\gamma_5(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}} \mathbb{E}([D_xF]^4) \lambda(\mathrm{d} x) \right]^{1/2}, \\[3pt]\gamma_6(F) &\,{:\!=}\, \frac{1}{\mathbb{V}ar(F)} \left[ \int_{{\textbf{X}}^2} 6 \Big( \mathbb{E}([D_{x_1}F]^4) \mathbb{E}([D^2_{x_1,x_2}F]^4) \Big)^{1/2} + 3 \mathbb{E}([D^2_{x_1,x_2}F]^4) \lambda^2(\mathrm{d}(x_1,x_2)) \right]^{1/2}.\end{align*}
Proof of Theorem 4. We aim to deduce the bounds for
![]() $\gamma_i(F)$
above via the proof strategy for [Reference Last, Peccati and Schulte32, Theorem 6.1]. Using the definitions of
$\gamma_i(F)$
above via the proof strategy for [Reference Last, Peccati and Schulte32, Theorem 6.1]. Using the definitions of
![]() $c_1,c_2$
, as well as Hölder’s inequality, we have that
$c_1,c_2$
, as well as Hölder’s inequality, we have that
Applying these bounds, together with further applications of Hölder’s inequality, gives that
![]() $\gamma_1(F) \leq W_1$
and
$\gamma_1(F) \leq W_1$
and
![]() $\gamma_2(F) \leq W_2$
. Note that
$\gamma_2(F) \leq W_2$
. Note that
![]() $\gamma_3(F)=W_3$
. This completes the proof for the Wasserstein bound in Theorem 4.
$\gamma_3(F)=W_3$
. This completes the proof for the Wasserstein bound in Theorem 4.
Subsequently, the bounds in (59) also yield that
![]() $\gamma_5(F) \leq W_5$
and
$\gamma_5(F) \leq W_5$
and
![]() $\gamma_6(F) \leq W_6$
. Using the equation at the end of the proof of [Reference Last, Peccati and Schulte32, Theorem 6.1], we obtain that
$\gamma_6(F) \leq W_6$
. Using the equation at the end of the proof of [Reference Last, Peccati and Schulte32, Theorem 6.1], we obtain that
where
Using the trivial inequality
![]() $\mathbb{P}(D_xF \neq 0) \leq 1$
, we get that
$\mathbb{P}(D_xF \neq 0) \leq 1$
, we get that
![]() $\gamma_4(F) \le W_4$
. Now the Kolmogorov bound in Theorem 4 has been obtained.
$\gamma_4(F) \le W_4$
. Now the Kolmogorov bound in Theorem 4 has been obtained.
Acknowledgements
The authors are very grateful for the detailed and useful comments received from two anonymous referees. These comments helped the authors to introduce a number of improvements to the paper. The work benefited from the visit of both the authors to Technion, Israel, and the authors are thankful to their host Robert Adler for the same. D. Y. is also thankful to the Department of Statistics at Purdue University for hosting him. D. Y. wishes to thank Subhojoy Gupta for some helpful discussions on hyperbolic geometry.
Funding information
T. O.’s research is partially supported by the NSF grant DMS-1811428. D. Y.’s research was supported in part by DST-INSPIRE Faculty fellowship and CPDA from the Indian Statistical Institute.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.