Published online by Cambridge University Press: 03 September 2019
We consider subgraph counts in general preferential attachment models with power-law degree exponent 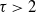 $\tau > 2$. For all subgraphs H, we find the scaling of the expected number of subgraphs as a power of the number of vertices. We prove our results on the expected number of subgraphs by defining an optimization problem that finds the optimal subgraph structure in terms of the indices of the vertices that together span it and by using the representation of the preferential attachment model as a Pólya urn model.
$\tau > 2$. For all subgraphs H, we find the scaling of the expected number of subgraphs as a power of the number of vertices. We prove our results on the expected number of subgraphs by defining an optimization problem that finds the optimal subgraph structure in terms of the indices of the vertices that together span it and by using the representation of the preferential attachment model as a Pólya urn model.