Article contents
The odds algorithm based on sequential updating and its performance
Published online by Cambridge University Press: 01 July 2016
Abstract
Let I1,I2,…,In be independent indicator functions on some probability space 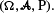 We suppose that these indicators can be observed sequentially. Furthermore, let T be the set of stopping times on (Ik), k=1,…,n, adapted to the increasing filtration
We suppose that these indicators can be observed sequentially. Furthermore, let T be the set of stopping times on (Ik), k=1,…,n, adapted to the increasing filtration 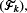 where
where 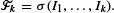 The odds algorithm solves the problem of finding a stopping time τ ∈ T which maximises the probability of stopping on the last Ik=1, if any. To apply the algorithm, we only need the odds for the events {Ik=1}, that is, rk=pk/(1-pk), where
The odds algorithm solves the problem of finding a stopping time τ ∈ T which maximises the probability of stopping on the last Ik=1, if any. To apply the algorithm, we only need the odds for the events {Ik=1}, that is, rk=pk/(1-pk), where 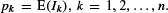 The goal of this paper is to offer tractable solutions for the case where the pk are unknown and must be sequentially estimated. The motivation is that this case is important for many real-world applications of optimal stopping. We study several approaches to incorporate sequential information. Our main result is a new version of the odds algorithm based on online observation and sequential updating. Questions of speed and performance of the different approaches are studied in detail, and the conclusiveness of the comparisons allows us to propose always using this algorithm to tackle selection problems of this kind.
The goal of this paper is to offer tractable solutions for the case where the pk are unknown and must be sequentially estimated. The motivation is that this case is important for many real-world applications of optimal stopping. We study several approaches to incorporate sequential information. Our main result is a new version of the odds algorithm based on online observation and sequential updating. Questions of speed and performance of the different approaches are studied in detail, and the conclusiveness of the comparisons allows us to propose always using this algorithm to tackle selection problems of this kind.
Keywords
MSC classification
- Type
- General Applied Probability
- Information
- Copyright
- Copyright © Applied Probability Trust 2009
References
- 8
- Cited by


