Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T04:36:17.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributions of ballot problem random variables

Published online by Cambridge University Press:  01 July 2016

Chern-Ching Chao  and
Norman C. Severo
Chern-Ching Chao*
Affiliation:
Academia Sinica
Norman C. Severo*
Affiliation:
State University of New York at Buffalo
*
∗Postal address: Institute of Statistical Science, Academia Sinica, Taipei 11529, Taiwan, Republic of China.
∗∗Postal address: Department of Statistics, State University of New York at Buffalo, Buffalo, NY 14214, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that in a ballot candidate A scores a votes and candidate B scores b votes, and that all the possible voting records are equally probable. Corresponding to the first r votes, let α r and β r be the numbers of votes registered for A and B, respectively. Let p be an arbitrary positive real number. Denote by δ (a, b, p)[δ *(a, b, ρ)] the number of values of r for which the inequality 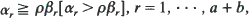, r = 1, ···, a + b, holds. Heretofore the probability distributions of δand δ* have been derived for only a restricted set of values of a, b, and ρ, although, as pointed out here, they are obtainable for all values of (a, b, ρ) by using a result of Takács (1964). In this paper we present a derivation of the distribution of δ [δ *] whose development, for any (a, b, ρ), leads to both necessary and sufficient conditions for δ [δ *] to have a discrete uniform distribution.

Keywords

DISCRETE UNIFORM DISTRIBUTIONLATTICE PATHS
Type
Research Article
Information
Advances in Applied Probability , Volume 23 , Issue 3 , September 1991 , pp. 586 - 597
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Part of this work was done while this author was at the State University of New York at Buffalo and at the University of Kentucky.

References

Aeppli, A. (1924) Zur Theorie verketteter Wahrscheinlichkeiten. Thesis, Zürich.Google Scholar
Andre, D. (1887) Solution directe du problème résolu par M. Bertrand. C. R. Acad. Sci. Paris 105, 436–437.Google Scholar
Barbier, E. (1887) Généralisation du problème résolu par M. Bertrand. C. R. Acad. Sci. Paris 105, 407.Google Scholar
Barton, D. E. and Mallows, C. L. (1965) Some aspects of the random sequence. Ann. Math. Statist. 36, 236–260.CrossRefGoogle Scholar
Bertrand, J. (1887) Solution d'un problème. C. R. Acad. Sci. Paris 105, 369.Google Scholar
Bizley, M. T. L. (1954) Derivation of a new formula for the number of minimal lattice paths from (0, 0) to (km, kn) having just t contacts with the line my = nx and having no points above this line; and a proof of Grossman's formula for the number of paths which may touch but do not rise above this line. J. Inst. Actuar. 80, 55–62.CrossRefGoogle Scholar
Bizley, M. T. L. (1967) Problem 5503. Amer. Math. Monthly 74, 728.Google Scholar
Dvoretzky, A. and Motzkin, Th. (1947) A problem of arrangements. Duke Math. J. 14, 305–313.CrossRefGoogle Scholar
Engelberg, O. (1965) Generalizations of the ballot problem. Z. Wahrscheinlichkeitsth. 3, 271–275.CrossRefGoogle Scholar
Filaseta, M. (1985) A new method for solving a class of ballot problems. J. Comb. Theory A 39, 102–111.CrossRefGoogle Scholar
Grossman, H. D. (1946) Fun with lattice points—4, 4a, 5. Scripta Math. 12, 223–225.Google Scholar
Grossman, H. D. (1950a) Fun with lattice points—21. Scripta Math. 16, 120–124.Google Scholar
Grossman, H. D. (1950b) Fun with lattice points—22, 23. Scripta Math. 16, 207–212.Google Scholar
Grossman, H. D. (1954) Fun with lattice points—25. Scripta Math. 20, 203–204.Google Scholar
Mohanty, S. G. (1979) Lattice Path Counting and Applications. Academic Press, New York.Google Scholar
Mohanty, S. G. and Narayana, T. V. (1961) Some properties of compositions and their application to probability and statistics I. Biom. Z. 3, 252–258.CrossRefGoogle Scholar
Narayana, T. V. (1979) Lattice Path Combinatorics with Statistical Applications. University of Toronto Press.CrossRefGoogle Scholar
Narayana, T. V. and Rohatgi, V. K. (1965) A refinement of ballot theorems. Skand. Aktuarietidskr. 48, 222–231.Google Scholar
Riordan, J. (1964) The enumeration of election returns by number of lead positions. Ann. Math. Statist. 35, 369–379.CrossRefGoogle Scholar
Srinivasan, R. (1979) On some results of Takács in ballot problems. Discrete Math. 28, 213–218.CrossRefGoogle Scholar
Takács, L. (1962a) A generalization of the ballot problem and its application in the theory of queues. J. Amer. Statist. Assoc. 57, 327–337.Google Scholar
Takács, L. (1962b) Ballot problems. Z. Wahrscheinlichkeitsth. 1, 154–158.CrossRefGoogle Scholar
Takács, L. (1963) The distribution of majority times in a ballot. Z. Wahrscheinlichkeitsth. 2, 118–121.CrossRefGoogle Scholar
Takács, L. (1964) Fluctuations in the ratio of scores in counting a ballot. J. Appl. Prob. 1, 393–396.CrossRefGoogle Scholar
Takács, L. (1967) Combinatorial Methods in the Theory of Stochastic Processes. Wiley, New York.Google Scholar
Takács, L. (1970) On the fluctuations of election returns. J. Appl. Prob. 7, 114–123.CrossRefGoogle Scholar
Whitworth, W. A. (1878) Arrangements of m things of one sort and n things of another sort under certain conditions of priority. Messenger of Math. 8, 105–114.Google Scholar