Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T07:22:34.854Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion approximations of Markov chains with two time scales and applications to population genetics, II

Published online by Cambridge University Press:  01 July 2016

S. N. Ethier  and
Thomas Nagylaki
S. N. Ethier*
Affiliation:
University of Utah
Thomas Nagylaki*
Affiliation:
University of Chicago
*
∗Postal address: Department of Mathematics, University of Utah, Salt Lake City, UT 84112, USA.
∗∗Postal address: Department of Molecular Genetics and Cell Biology, The University of Chicago, 920 East 58th Street, Chicago, IL 60637, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

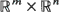For N = 1, 2, …, let {(XN (k), YN (k)), k = 0, 1, …} be a time-homogeneous Markov chain in . Suppose that, asymptotically as N → ∞, the ‘infinitesimal' covariances and means of XN([·/ε N]) are aij(x, y) and bi(x, y), and those of YN ([·/δ N]) are 0 and cl(x, y). Assume 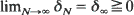and limN→∞ε N/δ N = 0. Then, under a global asymptotic stability condition on dy/dt = c(x, y) or a related difference equation (and under some technical conditions), it is shown that (i) XN([·/ε N]) converges weakly to a diffusion process with coefficients aij(x, 0) and bi(x, 0) and (ii) YN([t/ε N]) → 0 in probability for every t > 0. The assumption in Ethier and Nagylaki (1980) that the processes are uniformly bounded is removed here.

The results are used to establish diffusion approximations of multiallelic one-locus stochastic models for mutation, selection, and random genetic drift in a finite, panmictic, diploid population. The emphasis is on rare, severely deleterious alleles. Models with multinomial sampling of genotypes in the monoecious, dioecious autosomal, and X-linked cases are analyzed, and an explicit formula for the stationary distribution of allelic frequencies is obtained.

Keywords

DIFFUSION APPROXIMATIONSMARTINGALE PROBLEMRANDOM GENETIC DRIFTHARDY–WEINBERG PROPORTIONSRARE ALLELES
Type
Research Article
Information
Advances in Applied Probability , Volume 20 , Issue 3 , September 1988 , pp. 525 - 545
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported in part by NSF grant DMS-8403648.

Supported in part by NSF grant BSR-8512844.

†

In general, Ez[f(ZN(1))] denotes the integral of f with respect to the one-step transition function of ZN(·) starting at z; a similar convention applies to probabilities, variances, and covariances.

References

Ethier, S. N. and Kurtz, T. G. (1986) Markov Processes: Characterization and Convergence. Wiley, New York.CrossRefGoogle Scholar
Ethier, S. N. and Nagylaki, T. (1980) Diffusion approximations of Markov chains with two time scales and applications to population genetics. Adv. Appl. Prob. 12, 14–49.CrossRefGoogle Scholar
Ewens, W. J. (1969) Population Genetics. Methuen, London.CrossRefGoogle Scholar
Ewens, W. J. (1979) Mathematical Population Genetics. Biomathematics 9, Springer-Verlag, Berlin.Google Scholar
Fukushima, M. and Stroock, D. (1987) Reversibility of solutions to martingale problems. Adv. Math. Suppl. Stud. 9, 107–123.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M. (1980) Table of Integrals, Series, and Products. Corrected and enlarged edition. Academic Press, New York.Google Scholar
Guess, H. A. and Levikson, B. Z. (1977) The transient behavior of highly deleterious, nearly recessive mutant genes in finite populations. Unpublished ms.Google Scholar
Kawazu, K. and Watanabe, S. (1971) Branching processes with immigration and related limit theorems. Theory Prob. Appl. 16, 36–54.CrossRefGoogle Scholar
Kuklíková, D. (1978) Approximation of bivariate Markov chains by one-dimensional diffusion processes. Apl. Mat. 23, 267–279.Google Scholar
Lange, K., Gladstien, K., and Zatz, M. (1978) Effects of reproductive compensations and genetic drift on X-linked lethals. Am. J. Hum. Genet. 30, 180–189.Google ScholarPubMed
Li, W.-H. (1977) Maintenance of genetic variability under mutation and selection pressures in a finite population. Proc. Natl. Acad. Sci. USA 74, 2509–2513.CrossRefGoogle Scholar
Nagylaki, T. (1980) The strong-migration limit in geographically structured populations. J. Math. Biol. 9, 101–114.CrossRefGoogle ScholarPubMed
Nagylaki, T. (1982) Geographical invariance in population genetics. J. Theoret. Biol. 99, 159–172.CrossRefGoogle ScholarPubMed
Nagylaki, T. (1983) Evolution of a finite population under gene conversions. Proc. Natl. Acad. Sci. USA 80, 6278–6281.CrossRefGoogle Scholar
Nagylaki, T. (1985) Biased intrachromosomal gene conversion in a chromosome lineage. J. Math. Biol. 21, 225–235.CrossRefGoogle Scholar
Nagylaki, T. (1986) The Gaussian approximation for random genetic drift. In Evolutionary Processes and Theory, ed. Karlin, S. and Nevo, E., 629–642. Academic Press, New York.CrossRefGoogle Scholar
Norman, M. F. (1972) Markov Processes and Learning Models. Academic Press, New York.Google Scholar
Norman, M. F. (1975) Diffusion approximation of non-Markovian processes. Ann. Prob. 3, 358–364.CrossRefGoogle Scholar
Shiga, T. (1981) Diffusion processes in population genetics. J. Math. Kyoto Univ. 21, 133–151.Google Scholar
Skellam, J. G. (1949) The probability distribution of gene differences in relation to selection, mutation, and random extinction. Proc. Camb. Phil. Soc. 45, 364–367.CrossRefGoogle Scholar
Slatkin, M., Thomson, G., and Sawyer, S. (1979) Genetic drift in sex-linked lethal disorders. Am. J. Hum. Genet. 31, 156–160.Google ScholarPubMed
Watterson, G. A. (1962) Some theoretical aspects of diffusion theory in population genetics. Ann. Math. Stat. 33, 939–357; erratum 34, (1963), 352.CrossRefGoogle Scholar
Watterson, G. A. (1977) Heterosis or neutrality? Genetics 85, 789–814.CrossRefGoogle ScholarPubMed
Wright, S. (1949) Adaptation and selection. In Genetics, Paleontology, and Evolution, ed. Jepsen, G. L., Simpson, G. G., and Mayr, E., 365–389. Princeton University Press, Princeton.Google Scholar
Yamada, T. and Watanabe, S. (1971) On the uniqueness of solutions of stochastic differential equations. J. Math. Kyoto Univ. 11, 155–167.Google Scholar