Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-13T00:45:29.103Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence in mean of some characteristics of the convex hull

Published online by Cambridge University Press:  01 July 2016

Henk Brozius
Henk Brozius*
Affiliation:
Erasmus University Rotterdam
Get access Rights & Permissions [Opens in a new window]

Abstract

A sequence Xn, 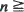1 of independent and identically distributed random vectors is considered. Under a condition of regular variation, the number of vertices of the convex hull of {X1, …, Xn} converges in distribution to the number of vertices of the convex hull of a certain Poisson point process. In this paper, it is proved without sharpening the conditions that the expectation of this number also converges; expressions are found for its limit, generalizing results of Davis et al. (1987). We also present some results concerning other quantities of interest, such as area and perimeter of the convex hull and the probability that a given point belongs to the convex hull.

Keywords

REGULAR VARIATIONPOINT PROCESSESPALM PROBABILITIES
Type
Research Article
Information
Advances in Applied Probability , Volume 21 , Issue 3 , September 1989 , pp. 526 - 542
Copyright
Copyright © Applied Probability Trust 1989 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This study was funded by the Netherlands Organization for the Advancement of Pure Research (N.W.O.).

References

Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Brozius, H. A. and De Haan, L. (1987) On limiting laws for the convex hull of a sample. J. Appl. Prob. 24, 852–862.Google Scholar
Carnal, H. (1970) Die Konvexe Hulle von n rotationssymmetrisch verteilten Punkten. Z. Wahrscheinlichkeitsth. 15, 168–176.Google Scholar
Davis, R., Mulrow, E. and Resnick, S. (1987) The convex hull of a random sample in Y2 . Stoch. Models 3, 1–27.CrossRefGoogle Scholar
Eddy, W. F. (1982) Convex hull peeling. COMPSTAT 5, 42–47.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications. Vol. II, 2nd edn. Wiley, New York.Google Scholar
Green, P. J. (1981) Peeling bivariate data. In Interpreting Multivariate Data, ed. Barnett, V., Wiley, New York, 3–19.Google Scholar
Jagers, P. (1973) On Palm probabilities. Z. Wahrscheinlichkeitsth. 26, 17–32.Google Scholar
Kallenberg, O. (1976) Random Measures. Akademie Verlag, Berlin.Google Scholar
Neveu, J. (1976) Processes Ponctuels. Ecole d'Eté de Probabilités de Saint-Flour. Lecture Notes in Mathematics 598, Springer-Verlag, Berlin.Google Scholar
Pickands, J. (1968) Moment convergence of sample extremes. Ann. Math. Statist. 39, 881–889.Google Scholar
Valentine, F. A. (1964) Convex Sets. McGraw-Hill, New York.Google Scholar