Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T06:49:23.629Z Has data issue: false hasContentIssue false
  • English
  • Français

An extremal property of FIFO discipline in G/IFR/1 queues

Published online by Cambridge University Press:  01 July 2016

Tetsuji Hirayama  and
Masaaki Kijima
Tetsuji Hirayama*
Affiliation:
University of Electro-communications, Tokyo
Masaaki Kijima*
Affiliation:
Tokyo Institute of Technology
*
∗Postal address: Department of Communications and Systems Engineering, University of Electro-communications, Chofugaoka, Chofu-shi, Tokyo 182, Japan.
∗∗Postal address: Department of Information Sciences, Tokyo Institute of Technology, Oh-okayama, Meguro-ku, Tokyo 152, Japan.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

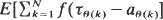In a recent paper by Shanthikumar and Sumita (1987), it is conjectured that the ergodic sojourn time of a customer in G/IFR/1 queues is minimized by FIFO (first in, first out) discipline in the sense of increasing and convex ordering. This paper shows that their conjecture is true. In fact, FIFO discipline minimizes for any non-decreasing and convex function f, where N is the (constant) number of arrivals, θ (k) is the customer identity of the kth departing customer, and an and τ n denote the arriving and departing times of the nth customer, respectively.

Keywords

IFR SERVICE TIMESINGLE-SERVER QUEUEDYNAMIC SCHEDULINGINTERCHANGE ARGUMENT
Type
Letters to the Editor
Information
Advances in Applied Probability , Volume 21 , Issue 2 , June 1989 , pp. 481 - 484
Copyright
Copyright © Applied Probability Trust 1989 

References

[1] Barlow, R. E. and Proschan, F. (1975). Statistical Theory of Reliability and Life Testing. Holt, Rinehart and Winston, New York.Google Scholar
[2] Hirayama, T., Kijima, M. and Nishimura, S. (1989). Further results for dynamic scheduling of multiclass G/G/1 queues. J. Appl. Prob. 26(3).Google Scholar
[3] Jackson, J. R. (1961) Queues with dynamic priority discipline. Management Sci. 8, 18–34.Google Scholar
[4] Kleinrock, L. (1976) Queueing Systems, Vol. 2. Wiley, New York.Google Scholar
[5] Ross, S. (1983) Introduction to Stochastic Dynamic Programming. Academic Press, New York.Google Scholar
[6] Royden, H. (1968) Real Analysis. Macmillan, New York.Google Scholar
[7] Schrage, L. (1974) Optimal Scheduling Disciplines for a Single Machine under Various Degrees of Information. Working Paper, Graduate School of Business, University of Chicago.Google Scholar
[8] Shanthikumar, J. G. and Sumita, U. (1987) Convex ordering of sojourn times in single-server queues: extremal properties of FIFO and LIFO service disciplines. J. Appl. Prob. 24, 737–748.CrossRefGoogle Scholar