Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T08:12:09.561Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperplans poissoniens et compacts de Steiner

Published online by Cambridge University Press:  01 July 2016

G. Matheron
G. Matheron*
Affiliation:
Centre de Morphologie Mathématique, Fontainebleau
Get access Rights & Permissions [Opens in a new window]

Abstract

A compact convex set in RN is Steiner if it is a finite Minkowski sum of line segments, or a limit of such finite sums, and then satisfies an extension of the Steiner formula. With each Poisson hyperplane stationary process A is uniquely associated a Steiner set M, and for any linear variety V, the Steiner set associated with 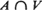is the projection of M on V. The density of the order k network Ak (i.e., the set of the intersections of k hyperplanes belonging to A) is linked with simple geometrical properties of M. In the isotropic case, the expression of the covariance measures associated with Ak is derived and compared with the analogous results obtained for (N — k)-dimensional Poisson flats.

Keywords

POISSON FLATSSTEINER COMPACT SETSSTEINER FORMULACONVARIANCE MEASURE
Type
Research Article
Information
Advances in Applied Probability , Volume 6 , Issue 3 , September 1974 , pp. 563 - 579
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

[1] Blaschke, W. (1936–1937) Vorlesungen über Integral Geometrie. Teubner, Leipzig.Google Scholar
[2] Hadwiger, H. (1957) Vorlesungen über Inhalt, Oberfläche und Isoperimetrie. Springer, Berlin.Google Scholar
[3] Matheron, G. (1972) Ensembles aléatoires, ensembles semi-markoviens et polyèdres poissoniens. Adv. Appl. Prob. 4, 508–541.Google Scholar
[4] Matheron, G. (1973) Un théorème d'unicité pour les hyperplans poissoniens. J. Appl. Prob. 11, 184–189.Google Scholar