Article contents
Optimal Bicubic Finite Volume Methods on Quadrilateral Meshes
Published online by Cambridge University Press: 29 May 2015
Abstract
In this paper, an optimal bicubic finite volume method is established and analyzed for elliptic equations on quadrilateral meshes. Base on the so-called elementwise stiffness matrix analysis technique, we proceed the stability analysis. It is proved that the new scheme has optimal 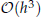 convergence rate in H1 norm. Additionally, we apply this analysis technique to bilinear finite volume method. Finally, numerical examples are provided to confirm the theoretical analysis of bicubic finite volume method.
convergence rate in H1 norm. Additionally, we apply this analysis technique to bilinear finite volume method. Finally, numerical examples are provided to confirm the theoretical analysis of bicubic finite volume method.
- Type
- Research Article
- Information
- Copyright
- Copyright © Global-Science Press 2015
References
- 3
- Cited by


