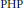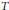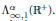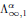6 results
25 - Unbounded Operators on Hilbert Spaces
- from Part IV - Banach Spaces
-
- Book:
- An Introduction to Functional Analysis
- Published online:
- 21 March 2020
- Print publication:
- 12 March 2020, pp 264-272
-
- Chapter
- Export citation
On the Adjoint and the Closure of the Sum of Two Unbounded Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 3 / 01 September 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 498-505
- Print publication:
- 01 September 2011
-
- Article
-
- You have access
- Export citation
On Operator Sum and Product Adjoints and Closures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 3 / 01 September 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 456-463
- Print publication:
- 01 September 2011
-
- Article
-
- You have access
- Export citation
UNBOUNDED 2-HYPEREXPANSIVE OPERATORS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 3 / October 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 613-629
-
- Article
-
- You have access
- Export citation
H∞ Functional Calculus and Mikhlin-Type Multiplier Conditions
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1010-1027
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
On Operators with Spectral Square but without Resolvent Points
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 1 / 01 February 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 61-81
- Print publication:
- 01 February 2005
-
- Article
-
- You have access
- Export citation