We consider the algebraic K-theory of a truncated polynomial algebra in several commuting variables, 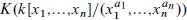 . This naturally leads to a new generalization of the big Witt vectors. If k is a perfect field of positive characteristic we describe the K-theory computation in terms of a cube of these Witt vectors on ℕn. If the characteristic of k does not divide any of the ai we compute the K-groups explicitly. We also compute the K-groups modulo torsion for k = ℤ.
. This naturally leads to a new generalization of the big Witt vectors. If k is a perfect field of positive characteristic we describe the K-theory computation in terms of a cube of these Witt vectors on ℕn. If the characteristic of k does not divide any of the ai we compute the K-groups explicitly. We also compute the K-groups modulo torsion for k = ℤ.
To understand this K-theory spectrum we use the cyclotomic trace map to topological cyclic homology, and write 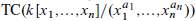 as the iterated homotopy cofiber of an n-cube of spectra, each of which is easier to understand.
as the iterated homotopy cofiber of an n-cube of spectra, each of which is easier to understand.

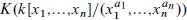 . This naturally leads to a new generalization of the big Witt vectors. If
. This naturally leads to a new generalization of the big Witt vectors. If 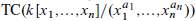 as the iterated homotopy cofiber of an
as the iterated homotopy cofiber of an 