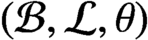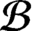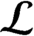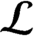1 results
CONDITION (K) FOR BOOLEAN DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 145-169
- Print publication:
- April 2022
-
- Article
- Export citation