We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the notion of tightly stationary sets which was introduced by Foreman and Magidor in [8]. We obtain two consistency results showing that certain sequences of regular cardinals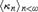 
${\langle {\kappa _n}\rangle _{n < \omega }}$ can have the property that in some generic extension, every ground-model sequence of fixed-cofinality stationary sets 
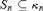${S_n} \subseteq {\kappa _n}$ is tightly stationary. The results are obtained using variations of the short-extenders forcing method.
