1 results
On lattices in semi-stable representations: a proof of a conjecture of Breuil
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 61-88
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation

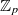 -lattices in semi-stable
-lattices in semi-stable 