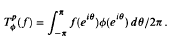1 results
Extremal problems in Hp
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-110
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation