We consider Schubert problems with respect to flags osculating the rational normal curve. These problems are of special interest when the osculation points are all real. In this case, for zero-dimensional Schubert problems, the solutions are “ as real as possible”. Recent work by Speyer has extended the theory to the moduli space 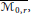$\overline{{{\mathcal{M}}_{0,\,r}}}$ allowing the points to collide. This gives rise to smooth covers 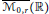$\overline{{{\mathcal{M}}_{0,\,r}}}\left( \mathbb{R} \right)$, with structure and monodromy described by Young tableaux and jeu de taquin.

In this paper, we give analogous results on one-dimensional Schubert problems over 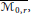$\overline{{{\mathcal{M}}_{0,\,r}}}$.Their(real) geometry turns out to be described by orbits of Schützenberger promotion and a related operation involving tableau evacuation. Over 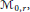${{\mathcal{M}}_{0,\,r}}$, our results show that the real points of the solution curves are smooth.

We also find a new identity involving “first-order” $\text{K}$-theoretic Littlewood-Richardson coefficients, for which there does not appear to be a known combinatorial proof.

Gaudin subalgebras are abelian Lie subalgebras of maximal dimension spanned by generators of the Kohno–Drinfeld Lie algebra . We show that Gaudin subalgebras form a variety isomorphic to the moduli space of stable curves of genus zero with n+1 marked points. In particular, this gives an embedding of in a Grassmannian of (n−1)-planes in an n(n−1)/2-dimensional space. We show that the sheaf of Gaudin subalgebras over is isomorphic to a sheaf of twisted first-order differential operators. For each representation of the Kohno–Drinfeld Lie algebra with fixed central character, we obtain a sheaf of commutative algebras whose spectrum is a coisotropic subscheme of a twisted version of the logarithmic cotangent bundle of .

Let $K$ be a function field and $C$ a non-isotrivial curve of genus $g\geqslant 2$ over $K$. In this paper, we will show that if $C$ has a global stable model with only geometrically irreducible fibers, then Bogomolov conjecture over function fields holds.