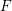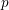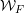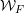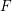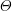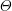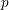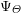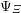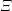Let $F$ be a non-Archimedean locally compact field of residual characteristic $p$ with Weil group ${\mathcal{W}}_{F}$. Let $\unicode[STIX]{x1D70E}$ be an irreducible smooth complex representation of ${\mathcal{W}}_{F}$, realized as the Langlands parameter of an irreducible cuspidal representation $\unicode[STIX]{x1D70B}$ of a general linear group over $F$. In an earlier paper we showed that the ramification structure of $\unicode[STIX]{x1D70E}$ is determined by the fine structure of the endo-class $\unicode[STIX]{x1D6E9}$ of the simple character contained in $\unicode[STIX]{x1D70B}$, in the sense of Bushnell and Kutzko. The connection is made via the Herbrand function $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}}$ of $\unicode[STIX]{x1D6E9}$. In this paper we concentrate on the fundamental Carayol case in which $\unicode[STIX]{x1D70E}$ is totally wildly ramified with Swan exponent not divisible by $p$. We show that, for such $\unicode[STIX]{x1D70E}$, the associated Herbrand function satisfies a certain functional equation, and that this property essentially characterizes this class of representations. We calculate $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6E9}}$ explicitly, in terms of a classical Herbrand function arising naturally from the classification of simple characters. We describe exactly the class of functions arising as Herbrand functions $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D6EF}}$, as $\unicode[STIX]{x1D6EF}$ varies over the set of totally wild endo-classes of Carayol type. In a separate argument, we derive a complete description of the restriction of $\unicode[STIX]{x1D70E}$ to any ramification subgroup and hence a detailed interpretation of the Herbrand function. This gives concrete information concerning the Langlands correspondence.

Let $F$ be a $p$-adic field and $K/F$ a finite, cyclic, tamely ramified field extension. We show, without any restriction, that base change from $F$ to K, in the sense of Arthur and Clozel, is compatible with the operation of $K/F$-lifting for simple characters defined by the authors in an earlier paper. This extends and completes the previous work, and represents a substantial step towards the goal of describing tamely ramified base change in terms of the structure theory of representations of Bushnell and Kutzko. We also give a consequence for the Langlands correspondence. The main step in the proof is to show that lifting of simple characters is compatible with automorphic induction, in the sense of Henniart and Herb, through an unramified extension. This is achieved via a new and independently interesting result concerning the conductor of a pair of supercuspidal representations. It gives a complete description of the minima of (a suitably normalized version of) the conductor when one of the representations is fixed. All results concerning the conductor are also valid for non-Archimedean local fields of positive characteristic.