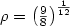Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Computer Science (1)

reversible automata

RAIRO - Theoretical Informatics and Applications (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

A Lower Bound For Reversible Automata
Pierre-Cyrille Héam
Journal:

RAIRO - Theoretical Informatics and Applications / Volume 34 / Issue 5 / September 2000

Published online by Cambridge University Press:

15 April 2002, pp. 331-341

Print publication:

September 2000
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
A reversible automaton is a finite automaton in which eachletter induces a partial one-to-one map from the set of states intoitself. We solve the following problem proposed by Pin. Given an alphabet A, does there exist a sequence of languages K n on A which can be accepted by a reversible automaton, and such that the number of states of the minimal automaton of K n is in O(n), while the minimal number of states of a reversible automaton accepting K n is in O(ρ n ) for some ρ > 1? We give such an example with $\rho=\left(\frac{9}{8}\right)^{\frac{1}{12}}$ 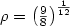.