A new class of iterated function systems is introduced, which allows for the computation of non-compactly supported invariant measures, which may represent, for example, greytone images of infinite extent. Conditions for the existence and attractiveness of invariant measures for this new class of randomly iterated maps, which are not necessarily contractions, in metric spaces such as 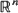 , are established. Estimates for moments of these measures are obtained.
, are established. Estimates for moments of these measures are obtained.
Special conditions are given for existence of the invariant measure in the interesting case of affine maps on 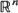 . For non-singular affine maps on
. For non-singular affine maps on 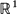 , the support of the measure is shown to be an infinite interval, but Fourier transform analysis shows that the measure can be purely singular even though its distribution function is strictly increasing.
, the support of the measure is shown to be an infinite interval, but Fourier transform analysis shows that the measure can be purely singular even though its distribution function is strictly increasing.

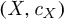
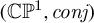
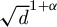
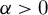
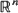 , are established. Estimates for moments of these measures are obtained.
, are established. Estimates for moments of these measures are obtained.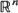 . For non-singular affine maps on
. For non-singular affine maps on 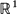 , the support of the measure is shown to be an infinite interval, but Fourier transform analysis shows that the measure can be purely singular even though its distribution function is strictly increasing.
, the support of the measure is shown to be an infinite interval, but Fourier transform analysis shows that the measure can be purely singular even though its distribution function is strictly increasing.