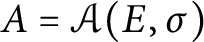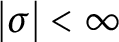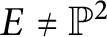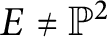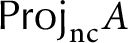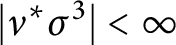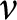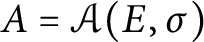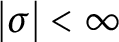For a three-dimensional quantum polynomial algebra $A=\mathcal {A}(E,\sigma )$ , Artin, Tate, and Van den Bergh showed that A is finite over its center if and only if $|\sigma |<\infty $ . Moreover, Artin showed that if A is finite over its center and 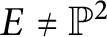$E\neq \mathbb P^{2}$ , then A has a fat point module, which plays an important role in noncommutative algebraic geometry; however, the converse is not true in general. 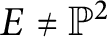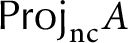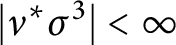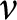In this paper, we will show that if $E\neq \mathbb P^{2}$ , then A has a fat point module if and only if the quantum projective plane ${\sf Proj}_{\text {nc}} A$ is finite over its center in the sense of this paper if and only if $|\nu ^{*}\sigma ^{3}|<\infty $ where $\nu $ is the Nakayama automorphism of A. In particular, we will show that if the second Hessian of E is zero, then A has no fat point module.